基于朴素Bayes组合的简易集成分类器①
2021-02-23宋丛威
宋丛威
(浙江工业大学 之江学院 理学院,绍兴 312030)
朴素Bayes 分类器是一种简单易用的分类器,在文本分类方面表现出色[1–4].垃圾邮件过滤是它最为成功的商业应用[5].到现在一直有人尝试把它应用于各种领域[6–9].
朴素Bayes 分类器建立在条件独立假设的基础上:

其中,一个只和x有关的系数被省略了.而这个假设比较强,通常无法被满足;计算出的后验概率和实际值也相差较大.不过,朴素Bayes 分类器却不会因此而受太大影响[10].实际上,朴素Bayes 分类器是一种可加模型[1],即有下述分解:
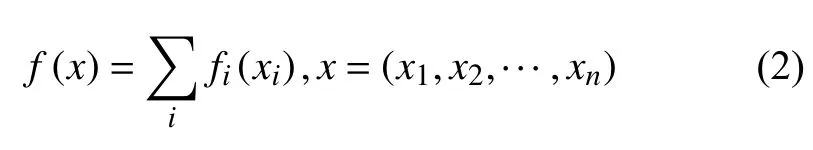
历史上人们提出了不少改进方案了[3,8].本文提出的改进方法解决了朴素Bayes 分类器的两个问题.
(1)通常朴素Bayes 分类器要么解决连续型的分类问题,要么解决离散型的分类问题,总之p(xi|c)的分布类型是同一的[11].而本文的方法不受此限制.
(2)在很多方面神经网络等机器学习算法和Bayes分类器是互补的.本文方法可以以非常简单的方式将两者结合起来.
1 朴素Bayes 组合分类器
本节主要推导朴素Bayes 组合公式,并简述分类器的构造.
1.1 朴素Bayes 组合公式
设x=(x1,x2,···,xm),即输入变量被分解成m部分,在条件独立假设的基础上,通过简单变形可得:

在算法设计上,下面的等价公式会比较好用:
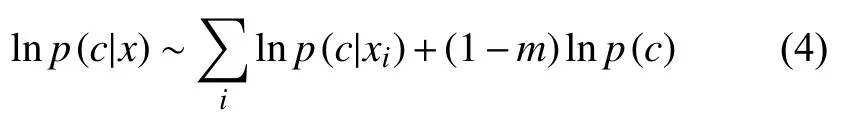
作为分量,xi不必是1维的;p(c|xi)都是独立计算的,互不干扰,而且也不是每一个都必须用Bayes 估计.如果第i项是用分类器fi进行估计的,那么:

其中,fi,c表示fi在c上的分量,代表lnp(c|xi)的估计.这就是说,只要用不同部分的数据独立训练多个训练分类器,然后简单求和就可以得到一个不错的分类器.这些分类器被称为基分类器(相当于线性代数中的基向量).这是一种特殊的可加模型,也可以看成一种简单的集成机器学习,即把fi(xi)看成是fi(Pix),其中Pi是x到xi的投影.我们把式(5)叫做朴素Bayes 组合公式,对应的分类器为朴素Bayes 组合分类器.
本文的方法最初是为了改进朴素Bayes 分类器而提出的,允许任意组合不同的朴素Bayes 分类器,如当面对包含连续变量和连续变量的机器学习问题时,可以组合基于Gauss 分布和基于多项式的朴素Bayes 分类器.但式(4)确实不是非要用朴素Bayes 分类器计算p(c|xi)不可,而且实验也支持用其他分类器能大大提高精确度.此时,严格地说它不再是朴素Bayes 分类器.
1.2 分类器的推广
作为加性模型的特殊形式,式(5)的一种简单推广是增加系数如下:
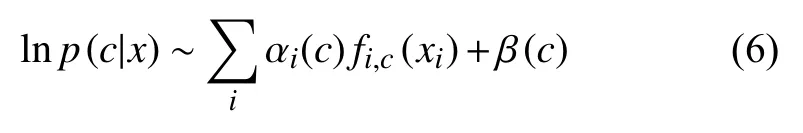
这些系数可以通过遗传算法获得,而初始种群可根据式(5)合理设置.这个推广将在以后的研究中实现.
本文的分类器还可以对缺失型数据进行分类,比如,只知道x=(x1,x2,···,xl),则只需计算:
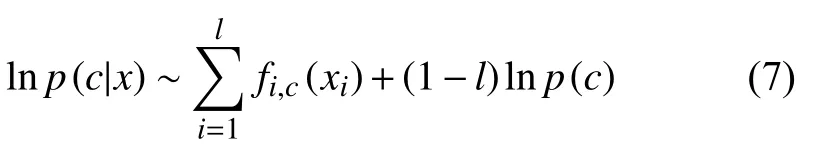
即只用其中l个基分类器.
输入变量的每个分量的分布通常是很不相同的,如果单纯采用单一分布下的朴素Bayes 分类器,效果会很差.本文的分类器允许人们根据每个变量的分布情况设计更有效的朴素Bayes 分类器,从而提高分类精度.
2 算法设计与实现
2.1 算法
算法基于式 (5),输入变量X会被分解成m部分,第i部分作为第i个基分类器的输入;这些分类器的输出则是共同的.根据分割后的样本,分类器被独立训练.具体的流程如算法1.

算法1.朴素Bayes 组合分类算法(准备数据集 )X,Y(1)选择一组基分类器,构造朴素Bayes 组合分类器;(X1,X2,···,Xm)(2)将输入数据X 分割为;(Xi,Y)(3)第i 个基分类器拟合;xp(c|x)(4)利用朴素Bayes 组合式(5),对任意输入 计算概率值;(5)根据概率值给出预测值.
其中第(3)步根据属性的数据类型进行分割,基本原则是分离离散与连续变量;第(4)步可以并行计算,获得较快的速度.
算法1 中离散型和连续型的分别通常是相对的.一般多数观测值的频率都比较小时,该变量就应被看作连续变量.
2.2 实现
本文采用Python 实现,主要依赖scikit-learn 机器学习库[12].本文算法基于和朴素Bayes 分类器一样的公式,因此它的实现只需继承scikit-learn 提供的实现朴素Bayes 算法的抽象类即可.
程序运行环境为MacOS10.15,Python3.7,scikit-learn 0.23.1.源代码、数据和实验结果已上传至GitHub (https://github.com/Freakwill/nb-ensemble).
3 实验分析
实验数据来自CCF 人工智能竞赛平台https://www.datafountain.cn/competitions/337.为了使它成为一个分类问题,根据数值大小已经把输出变量分为3 个等级,即分3 类.总共50000 条数据,抽出30%作为测试数据.
根据数据,输入变量被大致分为3 个部分:0-1 型,整数型,实数型.关键的原则依然是看数据的频数.选取适合的基分类器.集成的分类器将和这些基分类器(单独使用)进行比较.
所有模型都会被重复运行10 遍,计算两项指标(精确度与耗时)的均值;每次运行可能有微小的偏差.每种模型确实可以设置各项参数调整性能,但并不显著.除了神经网络设置了2000 次迭代,其隐层大小为8(朴素Bayes 组合中为5),其他都采用默认值.
实验结果(见表1)符合预期.无论耗时还是精确度,朴素Bayes 组合分类器都是介于朴素Bayes 分类器和其他分类器之间.该算法适用于那些允许牺牲一定精确度来节省时间的分类问题.如果对数据的分布做更深入的观察,设计更有针对性的基分类器,是可以获得更好的结果的.
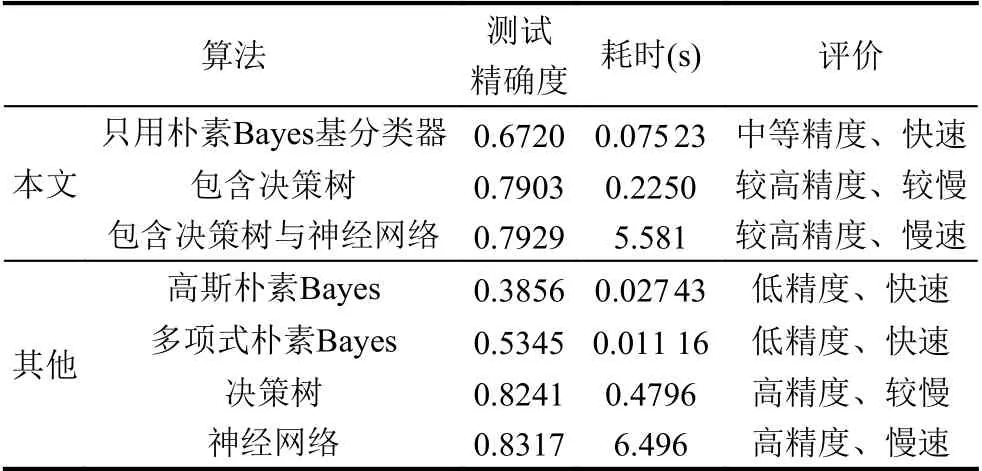
表1 不同算法比较
4 结论与展望
本文利用本朴素Bayes 组合公式设计出一种新的分类器,它是一种非常简便的集成机器学习方法.实验结果表明,算法在不要求高精确度的情况下,可以提高算法性能.如果需要在精确度和计算时间之间权衡,那么可以使用本算法.
如果基分类器都是朴素Bayes 分类器,那么朴素Bayes 组合的结果当然也是朴素Bayes 分类器.这样就可以轻易组合出能处理混合不同分布类型的数据集,如本文中的实验数据,存在至少3 种类型的分布.实验结果表明这种处理是成功的.因为基分类器并不限于朴素Bayes 分类器,所以对条件独立性的假设的依赖也减轻了,从而提高了精确度.实验还表明基分类器采用决策树、神经网络等分类器能获得更好的结果.
由于,本分类器以依然保留了不完全的条件独立假设,因此精确度的提升也是有限的,不能和某些成熟的算法竞争.但是,它的设计灵活简单,并具有并行性,和那些“成熟算法”相比,适当的设置可以大大缩减计算时间,而不会显著降低精确度.因此,这个算法适合那些对计算时间有较高要求的领域.
未来的研究主要沿着两个方向发展:设计更好的基分类器,如为那些含0 较多的数据选择更合理的分布进而设计相应的朴素Bayes 分类器;优化朴素Bayes组合公式突破现有的性能瓶颈.
