基于学习的并行绘制系统中数据集增强算法

李文静

（四川大学计算机学院，成都610065）

0 引言

计算机图形学广泛应用在计算机视觉、电子游戏、虚拟现实等领域，通过绘制系统，可构建出满足各领域需求的画面。而随着这些领域的发展，对绘制系统的输出分辨率、刷新频率以及绘制结果的真实感提出了更高的要求。由于单机绘制系统的计算能力无法满足以上要求，并行绘制系统随之被提出。并行绘制系统主要通过将绘制任务分配给多个处理器同时绘制的方法，来提升绘制系统的效率，以使系统实时地产生高分辨率，高刷新频率及高真实感的画面。

并行绘制系统中，负载平衡是实现实时并行的关键，其目的是将绘制任务尽量均匀的分配给各个绘制节点，使各绘制节点的绘制时间大致相同，从而缩短各绘制节点相互等待的时间，提升一帧图像的整体绘制效率。为了实现多个绘制节点的负载平衡，本文提出一种基于学习的并行绘制系统，主要思想是将绘制任务基于屏幕进行划分，并结合机器学习模型来进行每个子屏幕的负载预测，以此为基础找到一种令各子屏负载平衡的划分方式。通常来说，绘制算法提取的特征具有高维、维度间存在相关性的特点，并且系统对寻找负载平衡的划分方式这一过程有较高的效率要求。针对以上问题，本文选择具有天然并行性和能适应高维稀疏数据预测的随机森林（RF）模型[1]作为该系统中的机器学习模型。随机森林的预测准确度决定了并行绘制中的负载平衡程度，预测越准确，子屏之间的负载越平衡。而经验证明，机器学习中的训练集是影响机器学习模型好坏的主要因素[2]。因此，为得到一个好的训练集，通常基于已有的数据集，进行数据集增强。

数据集增强[3]是一种改善有监督学习模型的方法，它通过特定的变换来扩展训练集，从而使训练集变得更加完备。对于每一个新领域的数据集需求，已有的数据增强工具都需要经过非常仔细地设计、实现和测试才能获得变换集（即通过工具新合成的数据集）。针对本文并行绘制系统，本文提出了基于绘制算法特征的重采样策略，在初始采样的粗糙训练集的基础上，结合每个已有采样点的重要程度，生成新的采样点,加入到粗糙训练集里，以此得到更加完备的训练集。

1 算法实现

1.1 问题分析

在机器学习领域，一个好的训练集体现在与真实测试数据的匹配程度、完整性、无重复性、准确性和及时性等方面[4-5]。在本文的应用场景中，由于绘制系统本身的复杂性，负载函数将是一个高维函数，而训练集的大小和特征维度呈正相关。由此在数据采集阶段带来的一个重要问题就是，如何采集到有代表性的数据，使得可以将训练集的规模控制在一定的范围，而尽可能提高训练所得到的机器学习模型的性能。

由于本文的并行绘制系统应用于具有交互行为的游戏过程中，一个高质量的训练集应该需要捕捉到这种交互模式，确保与用户真实漫游得到的数据同分布。因此，本文采取一种模拟用户漫游习惯的方式来采集粗糙训练集，虽然这样的粗糙训练集能保证与测试集的视点信息分布一致，但其他绘制算法的分布是随机分布，而事实上，这些维度的特征对负载的影响程度可能并不比视点信息小。因此，如何采集到在各个维度的特征都具有代表性的数据，加入到训练集中使其更加完备成为本文研究的一个问题。针对以上问题，本文提出一个重采样方案，基于现有的粗糙训练集，以负载为依据来采集更具代表性的数据，加入到训练集中，以得到更加完备的训练集。

1.2 算法思想

粗糙训练集采取了一种基于用户漫游习惯的方式采集得到，因此，为了保证漫游习惯的分布，本文基于已有的粗糙训练集进行重采样。重采样的步骤是先确定重采样数据的特征，再根据特征得到负载，将两者结合成完整数据加入到训练集中。而其中，重采样数据的特征取决于该特征维度与负载之间的分布函数，但由于本文每个维度对负载的影响程度不一致，且每个维度之间具有相关性，会同时对负载产生影响，因此，无法将每一维视作独立的分布进行采样。基于以上分析，该问题转化为一个基于高维空间采样的问题，由蒙特卡洛重要性采样[6]的思想得知，某一区域的采样数目与负载变化呈正相关关系，负载变化越大的地方，采样点数目越多。而高维空间与负载的变化关系的拟合是一大难题，因此，本文将一个大的高维空间分割为小的“邻域”空间，针对每一个邻域空间，用负载的方差反映此空间的变化程度；然后，根据映射函数得到该空间需要采样的数目；再按照数目随机投射采样点，得到多个新的特征序列；最后根据这些特征序列进行绘制，得到响应负载（绘制时间），然后构成数据加入到粗糙训练集中。

1.3 算法实现

基于粗糙训练集，重采样过程主要包括特征的生成与负载的获取两个过程，具体流程如下：

（1）读取粗糙训练集DO中未被访问过的数据点，寻找其邻域范围内的数据点；

（2）根据找到的这些数据点，计算出方差v 并将v带入映射公式（1）得到需要采样的数目n。

（3）依据数目在该邻域范围内进行随机采样，得到特征序列集合{X1,X2,…,Xn} ，其中，Xi=( x1,x2,…,xm)，xi为第i 维特征，m 为特征维度；

（4）将特征序列逆转到并行绘制系统中的原始序列，传给系统进行绘制，得到对应的负载{Y1,Y2,…,Yn}；

（5）将特征序列和负载组合成数据集合{S1,S2,…,Sn} ，加入到重采样训练集DIs中。

（6）检测粗糙训练集DO中的点是否被全部访问，若是，则将DO和Dis合成为一个大的训练集D；否则，返回步骤（1）。

在本文的算法流程中，关键在于以下两点：①如何确定点的邻域；②得到新的特征序列后，如何逆转成绘制系统可用的原始序列。

由本文算法思想可知，“邻域”即为每个点周围的空间。对于量纲一致的维度来说，可以利用欧氏距离来确定邻域[7]，但是对于本文的应用场景，几乎每一维特征的量纲都不一致。因此，本文提出了利用相对AABB 的方法确定邻域，相对AABB 的大小由每一维空间的范围和比例参数σ 决定。首先，将所有数据的每个维度的范围保存下来得到{R1,R2,…,Rm}，利用σ确定相对AABB；然后针对数据点，基于相对AABB 能得到一个空间范围，即为该数据点的邻域。

特征序列转原始序列，依赖于特征序列和原始序列的格式，而其中，特征序列的格式与实验场景的算法相关。本文采用了光源链表（Light Linked List，LLL）算法，顺序独立透明（Order Independent Transparency，OIT）算法和屏幕空间环境光遮蔽（Screen Space Ambient Occlusion，SSAO）算法，基于这些图形绘制算法，本文用于学习的特征如表1 所示；而表2 展示本文绘制系统中原始序列的组成形式。

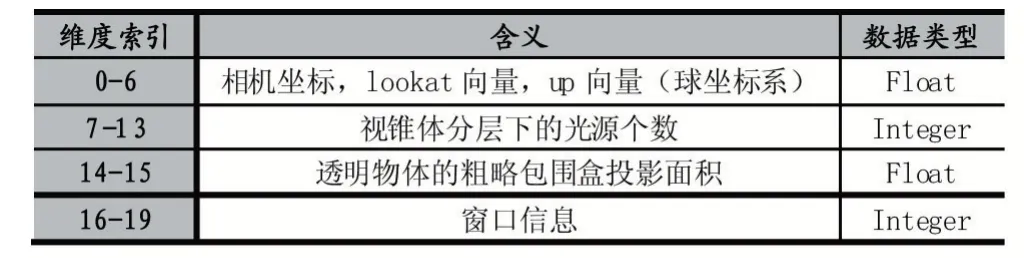
表1 特征序列的构成

表2 原始序列的构成

通过两个形式的对应关系，特征序列转化为原始序列主要包括下面几个步骤：首先，将7 维的相机信息转换为9 维，由于相机坐标不变，主要是将球坐标系中的look at 和up 向量转换为世界坐标系中的look at 和up 向量。由于相机up 向量一直向上，因此Up=(0,1,0)；look at 向量的转换公式如（2），其中(α,β)表示球坐标系下的look at 向量，Eye 表摄像机所在位置，At 表示得到的look at 向量；然后，将光源信息由7维的分层个数转化为100 个光源的坐标，例如，对于距离范围为[Li,Li+1]的分层，其中一个光源的逆转化公式如（3）所示，其中，Δx,Δy表示经过光源中心点得到的平面的长，宽的一半（横切视锥体并且与近平面平行），Dirx和Diry分别表示视点坐标系的x 轴和y 轴方向；另外，由于场景中的透明物体是静态的，因此可以直接获取到而不必通过特征来进行逆转化。通过上面的步骤，即可得到对应的原始序列。

2 实验结果

2.1 实验环境

PC 配置：Intel Core i3-4160 3.60GHz CPU，16G 内存，NVIDIA GeForce RTX 2060 显卡

场景配置：100 个动态光源，两个固定的透明物体

实验数据：基于用户漫游习惯采集38105 条数据作为原始粗糙训练集，3801 条作为测试集，另外，额外采取了61359 作为候选训练集。

2.2 实验结果

本文研究的目的在于得到更好的训练集，从而提升随机森林的预测准确率。因此，本实验通过对比两种训练集训练出的RF 的准确度，来验证本文数据集增强算法的有效性。RF 准确度可以用均方误差（MSE）[8]和决定系数（R2_Score）[9]进行评估。MSE 反映真实值和预测值的差异程度，其值越小，预测准确率越高；而R2_Score 反映回归模型的拟合程度，其值越大，拟合程度越高，预测准确率就越高。表3 为该实验对比结果。

表3 基于原始采样与重要性采样训练集的RF 性能对比

由以上结果看出，对于原始粗糙训练集来说，额外进行原始采样和重要性采样构成的训练集都对RF 的性能带来一定的提升，但是，对比两种额外采样方式，用重要性采样方式形成的训练集比原始采样方法构成的训练集更好。比如，用重要性采样的方式添加了52179 条数据到粗糙训练集后，MSE 为5.2706，R2_Score 为0.7688；而用原始采样方式添加了52244条数据到粗糙训练集后，MSE 为5.4602，R2_Score 为0.7605。前者比后者MSE 降低了0.1896，R2_Score 上升了0.0083。因此，可以得出，本文提出的重要性采样方式可以提升训练集，从而构建出更好的随机森林模型。

3 结语

本文提出了基于粗糙采样集进行重要性采样的数据集增强算法，意在得到更为完备的数据集，从而构建出更好的学习模型，以使基于学习的并行绘制系统表现出更好的性能。该算法在保证了采样的数据符合漫游习惯的同时，也能根据方差来采集到粗糙采样集缺失空间的数据，以获得更完备的数据集。最后，用实验证明了该算法的有效性。