利用经济生活元素开展数列教学

陈宏春

[摘  要] 高中数学教育中存在脱离生活的问题，随着社会的不断进步与发展，数学在日常生活中的应用已经越来越广泛，教师应该尝试多利用生活元素开展教学：一是熟悉的生活情境能有效地消除学生对陌生知识的抵触情绪;二是这样的教学模式能引导学生关注生活，培养学生观察生活的能力，让学生明白生活中处处有数学，鼓励学生在生活中不断学习数学. 文章中笔者将会以实例来展示利用常见的经济生活场景展开数列教学的方法.

[关键词] 生活元素教学;等差数列;等比数列;求和公式;通项公式

常常听到学生们开玩笑说道：“只要学完小学数学，就可以解决日常生活需求了，我们现在学的数学都没什么实际用途.”实际上，这样的说法并不适用于现代生活，它从侧面表现出了高中数学教育存在脱离生活的问题. 随着社会的不断进步与发展，数学在日常生活中的应用已经越来越广泛，教师应该尝试多利用生活元素开展教学：一是熟悉的生活情境能有效地消除学生对陌生知识的抵触情绪，从而使得学生能以更大的激情和更浓厚的兴趣投入学习中;二是这样的教学模式能引导学生关注生活，培养学生观察生活的能力，让学生明白生活中处处有数学.

数列是高中数学知识结构中的重要部分，能很有效地锻炼学生观察归纳和计算的能力. 数列的知识在经济生活中十分实用，下文中笔者将会以实例来展示利用常见的经济生活场景展开数列教学的方法.

银行存款利息问题

高中阶段的学生对于银行存款问题并不陌生，笔者曾在介绍完等比数列通项公式之后，让学生尝试应用通项公式的相关知识解决银行存款利息计算的问题.

师：假设你们每年有一万元用于储蓄，有两家银行分别提出了自己的利息策略. A银行采取无复利模式，每年提供本金7%的利息;B银行采取复利模式，每年提供上一年本息合计4%的利息. 在不考虑通货膨胀的情况下，请同学们相互讨论一下怎样规划才能使这笔资金得到的利息最多，看看你们是不是理财小能手.

在看见这样富有生活气息的问题后，学生们纷纷表现出了浓厚的兴趣，课堂讨论氛围十分热烈. 在学生大致讨论了一段时间后，笔者搜集了以下几种比较有代表性的储蓄方案.

方案A：一半的钱放在A银行，一半的钱放在B银行.

方案B：把所有的钱放在A银行.

方案C：先把所有的钱放在A银行，一定年数后本息合计放入B银行.

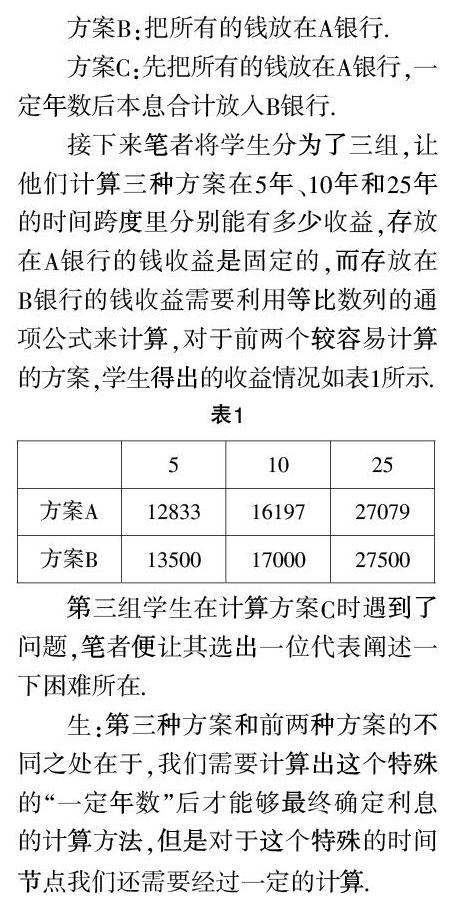
接下来笔者将学生分为了三组，让他们计算三种方案在5年、10年和25年的时间跨度里分别能有多少收益，存放在A银行的钱收益是固定的，而存放在B银行的钱收益需要利用等比数列的通项公式来计算，对于前两个较容易计算的方案，学生得出的收益情况如表1所示.

第三组学生在计算方案C时遇到了问题，笔者便让其选出一位代表阐述一下困难所在.

生：第三种方案和前两种方案的不同之处在于，我们需要计算出这个特殊的“一定年数”后才能够最终确定利息的计算方法，但是对于这个特殊的时间节点我们还需要经过一定的计算.

师：那么你们是怎么思考和计算的呢？

生：A银行虽然看起来利息率比较高，但是由于它不是复利型的方案，增加的利息是固定的，而随着总量的不断增加，B银行提供的方案产生的利息终有一年会超过A银行，于是我们一年一年地进行计算，对比A银行、B银行的利息差异.

师：的确，随着总量的增加，原本看似收益更小的B方案最终带来的收益反而会更多，思路是正确的，但是你们不觉得一年一年地进行计算是一件“吃力不讨好的事”吗？试着利用等比数列通项公式的知识来解决这个问题.

生（经过一段时间的思考）：那我们只要求解不等式10000+700n≤10000·（1.04）n（n∈N）即可.

师：很好，等比数列的通项公式正可以起到这样化繁为简的作用.

接下来教师带领着全班同学一起计算了第三种方案的收益情况，学生们十分投入和认真.

分期付款方案选择问题

问题情境：小王想要在工作之余成为一名兼职的滴滴司机，现要买一辆汽车，已知该汽车的总价值为115000元，全款买车不需要额外的钱，分期付款的方案如下：先交15000元的首付金，接下来的每一个月付5000元和余款利息，余款利息的计算公式为：利息=余款×1%. 如果小王手上的活动资金能够付得起首付却不能全款买下这辆车，20个月后才能全款买下，试问：小王平均每月要通过兼职司机這份工作赚多少钱，选择分期付款方式才更加经济？

情境分析：滴滴出行是学生们生活中常用的软件，以此为问题的情境能极大程度上调动起学生探索研究的欲望.

问题解答：先计算分期付款模式下的总付款. 根据题干信息易知，需要20个月才能最终还清所有的钱，假设第n个月小王需要付的金额数为an，则可以推断出an=6000-50（n-1）（n=1，2，…，n），因此该数列的和加上首付便是小王应该付的总额. 因为S20=110500，所以小王最终总付款为125500元，对比原价多付了10000元，因此小王需要每月通过兼职赚10000÷20=500（元）才更加经济.

企业经营利润问题

问题情境：某企业需要进行技术升级投资，现有两种方式可供选择.

方案A：一次性向银行贷款一千万元，第一年能够为企业增加一百万元的收益，往后收益逐年增加30%;

方案B：每一年都向银行贷款一百万元，往后第n年的收益为50（n+1）万元.

假设这两种方案中贷款的使用年限相同，皆为k（9≤k≤11，k∈N）年，到达期限之后公司需要连本带息一次性偿还，已知银行按年利率10%复利收取贷款利息，请问：出于净利润最大化考虑，公司应该选择哪种方案？

问题解答：（注：方便计算，下面所有数据皆以“百万元”作为单位）

方案A：分析收益情况易知，该方案的收益按年份成等比数列，根据首项为1和公比为3的条件可知，前n年的收益总和为（百万元），且可计算得银行贷款本息合计为10×1.1n（百万元），因此最终的净利润为-10×1.1n（百万元）.

方案B：该方案下的收益数据成等差数列（首项为1，公差为0.5），根据等差数列求和公式易得其前n项和为n+×0.5（百万元），而每一年的贷款本息合计成等比数列，总额为11×（1.1n-1）（百万元），因此净利润为n+×0.5-11×（1.1n-1）（百万元）.

当使用年限为9时，方案A的净利润为8.44百万元，方案B的净利润为12.06百万元，所以选择方案B公司所得净利润更高;

当使用年限为10时，方案A的净利润为16.68百万元，方案B的净利润为14.97百万元，所以选择方案A公司所得净利润更高;

当使用年限为11时，方案A的净利润为27.87百万元，方案B的净利润为18.12百万元，所以选择方案A公司所得净利润更高.

情境分析：该问题综合考察了等差数列、等比数列的求和公式，有利于帮助学生对比两种求和公式的异同.

植树造林增长率问题

问题情境：假设某地有2200亩荒地可以用来植树，若第一年年初植树100亩，往后逐年递增50亩，假设这些树木都能够成活，那么需要花多少年才可以把这片荒地种满绿树呢？若每一亩绿树在刚种下时有2m3的木材量，且每年木材量都会增长20%，试问：在实现全面绿化那一年的年底该地区木材总量为多少？

问题解答：将荒地完全绿化也就是要使得每一年的植树面积累加起来等于荒地的面积，根据题干条件易知，每一年绿化的面积成等差数列，因此根据求和公式可得前n年的绿化总面积为100n+25n（n-1），即要使100n+25n（n-1）=2200，可解得年数为8.

假设用an表示第n年种下的木材量，将木材量从最后一年向第一年逆推可得，最后一年年底每一年积累下来的木材量分别为2a8·1.2，2a7·1.22，2a6·1.23，…，2a1·1.28，将其求和便可得第九年年底的木材总量了.

注意点总结

（1）去繁存简，突出重点. 生活中的实际事件情况一般比较复杂，教师没必要将其都呈现出来，而是应该结合教学知识的需求，适当简化事件干扰因素，突出与教学目标最契合的点.

（2）教师引导，学生主导. 学生在接触到生活元素時一般会比较激动，教师要注意设置一些关键性的引导问题，防止学生注意力飘到无关紧要的地方去.

（3）情境引导，深度参与. 如第一点所示，教师在利用生活元素进行教学时，不妨建构一些可以让学生更有代入感的情境，这样的情境引导会让学生更加积极地投入研究.

（4）注意观察，结合时代. 高中生的生活阅历毕竟有限，教师在选取情境时要注意贴近学生的视角和生活.