在数学单元起始课中实现“思维的教学”

2020-04-07王华

江苏教育·中学教学版 2020年2期

【摘要】数学单元起始课要实现思维的教学，需正确把握三个关系，即动手与动脑之间的关系，即时思考与长时间思考之间的关系、各种思维品质之间的关系，从而改进学生的思维方式，让学生逐步学会更清晰、深入、全面、合理地思考问题。

【关键词】动手与动脑；思维品质；初中数学

【中图分类号】G633.6【文献标志码】A【文章编号】1005-6009（2020）11-0048-05

【作者简介】王华，江苏省镇江市丹徒区石马中学（江苏镇江，212113）副校长，高级教师，江苏省“333高层次人才培育工程”培养对象，镇江市学科带头人。

数学单元起始课，即数学单元开篇的第一节课，是整个单元学习的起点。起始课作为一个单元留给学生的“第一印象”，承担着激发学生的学习热情、培养学生学习兴趣的责任。在教学过程中，教师常常根据单元特点创设问题情境，通过设置合适的数学活动，如数学实验等，让学生经历观察、操作、计算、推理等过程，对本章将要学习的内容结构有一个大致的了解。

但由于一节课需让学生领略整个单元的内容结构（如概念、性质及应用）及贯穿始终的思想方法，课堂容量较大。现实中经常看到这样的现象：学生一直在做，一直在算，一直在动手，但就是不想！然而“数学归根到底是自己思考的产物”（陈省身语），因而单元起始课的教学必须将学生的动手与动脑结合起来，将思维的学习与具体数学知识内容的学习结合起来，帮助学生学会思维，并逐步学会想得更清晰、更深入、更全面、更合理。

“中心对称图形”是苏科版八年级下册第九章学习内容，具体包括：（员）图形的旋转的概念和性质；（圆）研究圖形的旋转的“特例”，即中心对称、中心对称图形；（猿）旋转知识在数学内部的应用，即用旋转、中心对称的概念和性质研究一些特殊平面图形的性质，解决数学问题；（源）将旋转知识应用于认识和解决现实问题。可见，图形旋转的概念和性质是本单元的基础，最为重要。

本节课是“中心对称图形”单元起始课，要求学生经历在一系列数学活动中发现问题、提出问题、分析问题、解决问题的过程，从中抽象出图形旋转的概念，并探寻几何图形性质研究的一般方法，为进一步探究旋转的特例及相关图形的性质提供策略，构建中心对称图形这一章的研究思路。因此，笔者注意从学生的数学现实及思维特点出发，通过设计数学实验，丰富思维活动，正确把握动手与动脑之间的关系，即时思考与长时间思考之间的关系、各种思维品质之间的关系，从而尝试改进学生的思维方式。

一、把握动手与动脑之间的关系

对于这里所说的“动手”，我们应作广义的理解：这不仅是指具体的实物操作，如旋转三角尺等，也包括各种数学运作，如让学生对研究对象进行度量，乃至各种各样的计算。南京大学教授郑毓信认为，教师在教学中往往特别重视学生“动手”，却忽视了如何能够促使他们更为积极地去“动脑”，忽视了帮助学生逐步学会想得更深、更合理、更清晰。咱1暂在“动手”之前教师需围绕：“为什么要动手”“事实上在做什么”“动手究竟产生了怎样的效果”三个问题让学生“动脑”，从而调动学生各种感官参与数学活动，根据提供的现实材料，经历动手操作、观察现象、提出猜想、验证结论等环节，体验“知识从何而来”“知识是什么”“知识向何而去”的完整数学学习过程。

本课作为“中心对称图形”的单元起始课，内容庞杂，其中图形旋转的概念最为基础与核心。我们知道，概念教学的核心就是让学生经历概念本质特征的概括过程，让学生根据具体事例，经历观察、操作、思考等过程，从中抽象出概念的本质特征。而图形旋转的本质特征是旋转中心、旋转角度、旋转方向“三要素”，因此本节课为探究旋转“三要素”定向设计了数学实验：让学生任意画一个吟ABC，并制作一个与之全等的三角形硬纸片，（1）将三角形纸片绕点A旋转 30毅，得到的结果怎样？（2）让它分别绕点A和点B逆时针旋转30毅，得到的结果一样吗？（3）让它绕点A逆时针旋转，得到的图形有多少个？（4）给定怎样的条件才能使旋转后的图形唯一确定？显然，经历上述4步的动手动脑比“看图归纳共同特征”更能凸显并提炼旋转的本质特征。

学生通过操作（1）明白了旋转方向不确定，可得出两个不同位置的图形；操作（2）明白了旋转中心不确定，可得出两个不同位置的图形；操作（3）明白了旋转角度不确定，可得出无数个不同位置的图形，进而引发对“如何唯一确定旋转后图形”的必然追问和思考，达到了“导而弗牵，强而弗抑，开而弗达”的境界。这样的手脑结合，使学生经历探究、反思、感悟、发现的过程，而旋转的概念慢慢“长”出，从而让学生回到“知识发生的现场”。

当然，上述4步骤的设计还有如下的考量，即让学生不仅仅明白“为什么要动手”，还要知道怎样设计操作流程才能达到效果。显然，根据图形旋转的概念，其旋转后图形的确定需要三个变量的同时确定，因此为了感受旋转“三要素”，在实验设计时，可采用控制变量法，将其中的两个变量加以确定，进而感受图形受第三个变量变化的影响，从而抽象出概念的本质特征。学生获得了这样的认知，做到“知其然，更知其所以然”，思维便能得到发展。

二、把握即时思考与长时间思考之间的关系

日本数学家、菲尔茨奖获得者广中平佑在《创造之门》一书中曾明确指出：思考问题的态度有两种。从专业角度看，一种是花费较短时间的即时思考型，一种是较长时间的长期思考型。所谓的思考能人，大概就是指能够根据思考的对象自由自在地分别使用这两种类型的思考态度的人。

郑毓信教授以康纳曼的工作作为直接背景，赋予了即时思考与长时间思考一些新的含义：

起始课强调激发学生的学习兴趣，培养学生参与学习的积极性与主动性，课堂往往呈现出热闹的氛围，学生一般采取即时思考的方式解决问题。但课堂不能只追求热闹的场面，必须处理好学生独立思考与合作学习、积极交流之间的关系，毕竟“数学是自己思考的产物”。综上可见，起始课也应努力追求另一种课堂境界，即营造安静的课堂、思维的课堂、开放的课堂，培养学生长时间思考的习惯与能力。

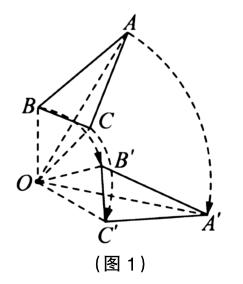
例如，教材在得出图形旋转的概念后，立即设置了探究性质的活动。如图1，吟ABC绕点O旋转到吟ABC的过程中，它的形状、大小没有改变，图1中还有哪些相等的线段、相等的角？根据这样的问题，学生能够快速地得出教师需要的答案，引出旋转的性质。但我们不能忽视这样一个重要的问题，就上述内容的教学而言为什么要突出“形状、大小是否改变”“有哪些相等的线段、相等的角”这样的信息？或者说，这样的信息究竟从哪里来？是怎么想到要从这些角度研究性质的？如果这些问题解决了，学生就不仅能探究出这几个性质，而且还会思考“还有哪些性质？”更重要的是能从中得到“如何研究性质”的锻炼。那么如何才能让学生不仅做得到，而且想得到呢？

笔者以为，与教材设置的问题相比，以下的问题引领更为恰当：（1）你认为研究旋转的性质是要研究什么？（2）具体而言是要研究什么呢？对应元素之间有什么关系？（3）对应元素有哪些？它们在形状、大小和位置方面有什么不变性？（4）观察旋转前后的两个图形，你能立即得到它们有哪些不变性？对应点的不变性怎么体现？这些问题是让学生知道，旋转的性质就是研究旋转前后两个图形的关系，图形变化中的那些不变性，具体而言就是旋转前后两个图形对应元素在形状、大小和位置关系方面的不变性。通过上述问题的设置与解决，让学生养成有序思考的习惯，赋予学生“想得到”的能力。

当然，这里还存在一个问题，即一旦引入某个概念，如图形的旋转，我们往往就会急于让学生通过动手操作去发现它们的性质，却没有认识到其中的很大一部分特性是相关概念的直接推论。本节课关于图形旋转前后对应点的不变性是教学的重难点，学生很难发现并表述清楚，教师要适时引导学生“从概念出发”思考性质，也就是要有利用“三要素”研究性质的意识。综上，学生不仅获得了图形的旋转的性质，更重要的是有了进一步探究旋转的特例及相关图形性质的策略与能力，在具体数学内容的学习中训练学生长时间思考的能力，促进其思维的发展。

三、把握各种思维品质之间的关系

相对于对具体数学思想方法的学习，通过单元起始课实现思维的教学应当更加重视学生思维品质的提升，包括思维的严密性（合理性）与深刻性，思维的整体性与结构性，以及思维的自主性与创新性。在起始课教学中，各个思维品质的提升不是互相孤立存在，它们之间密切相关，这一系列思维品质被看成理性思维最为重要的内涵。从数学教育的更大背景来说，我们应当努力追求的一个更高目标是不仅应帮助学生逐步学会理性地思维，也应促成他们由理性思维逐步走向理性精神，从而真正成为一个高度自觉的理性人。咱圆暂

1.提升学生思维的严密性和深刻性。

思维的严密性和深刻性是理性思维的重要因子。正如美国数学家R·柯朗和H·罗宾所说：数学，作为人类思维的表达形式，反映了人们积极进取的意志、缜密周详的推理及对完美境界的追求。逻辑的严密性是数学学科的重要特点，数学学习需关注学生的思维严密性（合理性），但又不能只停留在“是什么”的阶段，还需明白“为什么”。对“为什么”的追问可以看成是提升学生思维深刻性的一个重要方面。

例如，教师引导学生“从概念出发”探究旋转前后图形对应点的不变性时，先研究一组对应点的性质（即对应点到旋转中心的距离相等，对应点与旋转中心连线所成的角是旋转角），再到两组对应点的性质（即两组对应点分别与旋转中心连线所成的角相等）。像这样的有序思考不仅是逻辑严密的表现，从另一个角度来看，也能帮助学生提升思维的深刻性。另外，围绕“图形的旋转”概念与性质探索的“长时间思考”，对为什么研究旋转的性质就是要研究“形状、大小是否发生改变？”“有哪些相等的线段、相等的角？”对这类问题地不断追问，既能促使学生的思考合乎理性，也能将学生的思维引向深刻。

2.重视学生思维的整体性与结构性。

数学是整体的，其主要表现为数学知识内容的系统性和结构化。任何数学内容都来自某一系统，从属于某一结构。从结构的角度来把握所学习的数学内容，不仅能凸显内容的实质，建立内容之间的联系，而且有利于学生形成“从结构的角度把握事物本质”的结构化思维。咱3暂

如图2是“中心对称”这一单元的内容结构，有了前面图形的旋转概念和性质的研究经验，即研究性质需从概念出发，进而研究构成图形的元素及相关元素之间的关系，学生便能将图形旋转寅特例（性质）寅应用（平行四边形等、实际问题）等内容的研究方法一线串通，主动探究几何图形的性质，从而促进思维的迁移，获得研究方法的结构化。

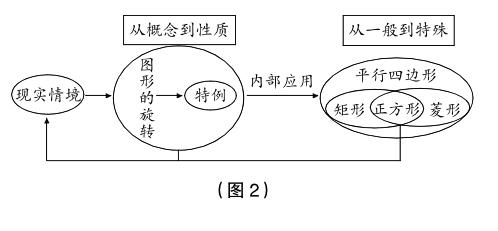
另外，本单元内容的设置整体上遵循了从一般到特殊的编写体例，如从图形的旋转到成中心对称，从中心对称图形到平行四边形，从平行四边形到特殊的平行四边形。其中，每一个特例的概念与性质都是建立在前一个上位概念与性质的基础之上。起始课不需要面面俱到，但对于这样的逻辑关系一定要给学生阐述清楚，让學生“见树木又见森林”。这样学生就会获得一般的研究方法，如研究成中心对称的两个图形的性质，就能想到图形旋转的性质，发现其具备图形旋转的一切性质，并“从概念出发”思考其“特别之处”。其余特例的研究亦是如此。教师可以根据起始课的特点，引导学生用不同的方式来表达数学的整体结构（如图2），发展学生的整体性思维、结构化思维、系统性思维，让学生获得学习数学的重要“法宝”，起到事半功倍的效果。

3.实现学生思维的自主性与创新性。

数学是人类文化的有机组成部分，它和其他文化一样，彰显着人的主体精神与创造性，散发着自身迷人的学科气息。因而，数学课堂上应特别关注学生的主体参与，在探究、反思、感悟、发现中去粗取精、去伪存真、由表及里、化繁为简，让知识慢慢“长”出来，让学习真正发生。而思维的创新不应简单地被等同于与众不同，其主要表现为对已有工作的不断优化，包括不同意见的适当整合。

本课在探究图形旋转的性质之前设置了这样一个活动，利用准备好的透明纸、白纸、硬纸板、三角尺、大头针等，创造一个三角形旋转的情境。学生经过自主探究，会先形成三种设计方案———

第一种方案是在白纸上描出一个三角尺的形状，即吟ABC，按着顶点A，将三角尺旋转一个角度，描出旋转后三角尺的形状，得到旋转前后的图形。

第二种方案是学生剪出一个三角形纸片，在白纸上描出该纸片的形状，在三角形内任取一点，用大头针固定，将三角形纸片旋转一定的角度，描出旋转后三角尺的形状，得到旋转前后的图形。

显然第二种方案比第一种方案更具有一般性，此时，学生观察到旋转中心从形上来到了形内，于是大胆想象、操作，创造了第三种方案：取一张硬纸片，在上面挖出一个三角形的洞，任意选硬纸片上一点为旋转中心，用大头针将其固定在白纸上，先描出三角形，然后绕着旋转中心转动硬纸片，再次描图，得到旋转前后的图形。这样得到的旋转图形，其旋转中心更具有普遍性，利于性质的进一步探究，而在整个设计过程中，学生从最初的方案开始自主设计、优化整合，表现出来的创新意识弥足珍贵。

总的来说，正如郑毓信教授所强调的：数学思维显然并非是思维的唯一可能形式，各种不同的思维形式，如文学思维、艺术思维、哲学思维、科学思维等，又都有其一定的合理性和局限性。从而，我们就不应唯一地去强调“帮助学生学会数学地思维”，“应当跳出数学，并从更为一般的角度去认识各种数学思想与数学方法的普遍意义”，“用思维方法的分析去带动具体知识内容的教学”。咱4暂尤其是单元起始课的教学，要让学生动手、动脑，在具体知识内容中感受整体，在结构中实现建构，在思维中学会思考。