基于几何随机的无人机空地信道模型

王亚文，朱秋明，陈小敏，仲伟志，成 能

（南京航空航天大学电磁频谱空间认知动态系统工业和信息化部重点实验室，南京，211106）

引 言

近年来，随着无人机（Unmanned aerial vehicle,UAV）在航拍、遥感监测、预警灾害和应急通信等领域的广泛应用，用户对机载通信链路的稳定性和可靠性也提出了更高要求。然而，UAV通信与传统移动通信的散射环境不同，UAV周围基本没有散射体且处于大范围立体空间的三维运动状态，空地信道传播场景变化明显，多普勒效应也更剧烈[1]。因此，建立精确、简单且符合真实场景的UAV空地信道模型，对实现UAV机载通信设备的方案设计、算法验证和性能评估具有重要意义。

当前针对UAV通信信道的模型包括确定性模型[2]（Deterministic model,DM）、非几何随机模型[3]（Non-geometrical stochastic channel model，NGSM）和几何随机模型[4-20]（Geometry-based stochastic channel model，GSCM）。其中，DM结合电磁波传播理论，利用数字地图预测不同传播路径参数，该方法比较复杂且受限于数字地图的精确性。NGSM利用实测数据获得参数化信道模型并进行统计描述，该方法不考虑具体的传播场景，信道的动态多普勒特性描述也不够完善。

GSCM利用电磁波传播理论模拟各个传播路径上的信号传输过程，由于其在复杂性和准确性之间取得平衡，成为近年来UAV信道建模的主流方法。比如，文献[5-10]假设地面端(Ground station,GS)的本地散射体服从特定的几何体分布，例如圆柱、球体和椭球体等，给出了针对UAV场景的三维GSCM平稳空地信道模型。测量数据表明，GS的移动会引起有效散射体的动态生灭，从而导致UAV信道呈现明显的非平稳特性[11]。因此，文献[12-15]通过将传播路径的生灭过程建模为马尔科夫随机过程，将非平稳特性引入传统的GSCM平稳信道模型。然而，文献[12-13]中假设UAV是静止的，文献[14-15]中假设UAV是匀速直线运动的，均不符合实际的UAV三维飞行场景。另外，上述文献[5-13]中信道模型只配置了2D天线阵列或均匀线性阵列，并且无法保证信道状态的相位连续性。

本文首先分析比较了现有UAV空地信道GSCM模型，并针对其不支持三维运动轨迹和三维天线的问题进行改进。此外，文中还详细分析UAV信道模型参数的时间演进算法。在此基础上，本文分析UAV非平稳信道模型的时变统计特性并与实测数据对比，验证了改进模型的准确性。

1 传统无人机空地信道模型

1.1 非平稳GSCM建模思路

图1给出了一个典型的三维立体空间无人机通信场景。以UAV与GS的下行通信信道为例，假设UAV周围不存在散射体，地面GS周围的散射体分布在规则或非规则几何体的表面。图中，vtx，vrx和vSn/Zn分别表示UAV、GS和散射体的移动速度；βLoStx(t)和 αLoStx(t)分别表示视距路径离开角的俯仰角（Elevation angle of departure,EAoD）和方位角（Azimuth angle of departure,AAoD）；βLoSrx(t)和αLoSrx(t)分别表示视距路径到达角的俯仰角（Elevation angle of arrival,EAoA）和方 位 角（Azimuthangleofarrival,AAoA）；βNLoStx,n,m(t)和αNLoStx,n,m(t)分别表示第n条非视距路径中第m条散射支路的EAoD和AAoD；βNLoSrx,n,m(t)和αNLoSrx,n,m(t)分别表示第n条非视距路径中第m条散射支路的EAoA和AAoA。

图1 无人机MIMO空地信道模型Fig.1 UAV MIMO air-ground channel model

GSCM核心思路是利用电磁波传播理论，将信道表示为多个传播路径之和，且各路径均包含多条传播射线。比如，UAV第q根发射天线与GS第p根接收天线之间的信道单位冲激响应可表示为

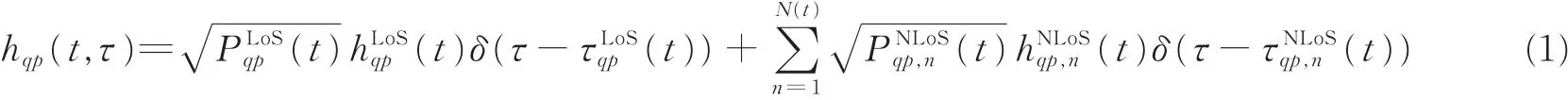
进一步地，视距路径复信道系数hLoSqp可表示为

式中：vtx/rx(t)=vtx/rx(t)[cos θtx/rx(t)cosφtx/rx(t),cosθtx/rx(t)sinφtx/rx(t),sinθtx/rx(t)]，θtx(t)和 φtx(t)分别表示UAV运动方向的俯仰角和方位角，θrx(t)和φrx(t)分别表示GS运动方向的俯仰角和方位角；T表示视距路径球形单位矢量；k=2π f0c0表示波束的数量，f0和c0表示载波频率和光速；φLoS是随机初始相位。非视距路径复信道衰落系数h可表示为

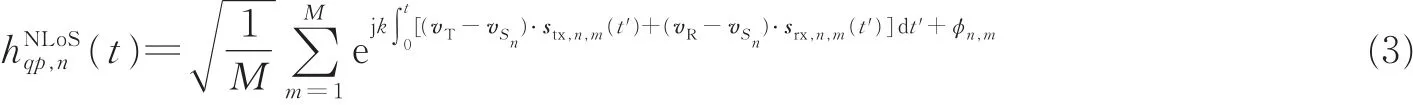
1.2 不同散射体分布模型比较

GSCM根据散射体分布特点可进一步分为规则形状（Regular shape,RS）和非规则形状（Irregular shape,IS）两类[16]。其中，RS-GSCM实现比较简单，该方法假设散射体服从特定几何体形状，如球体模型、圆柱体模型和椭球体模型。比如，令UAV和GS的位置分别为Dtx和Drx，圆柱体和球体中第n个散射体位置实测数据表明，EAoA和AAoA服从特定的统计分布，表1给出常见圆柱体和球体到达角的分布情况以及部分相应的球体参数。表中分别表示GS端的EAoA均值和AAoA均值，βRm表示EAoA的最大值；σ和κ表示分布函数的集散程度；I0(·)表示零阶贝塞尔函数；I1/2(·)表示零均值修正贝塞尔函数。在此基础上，可确定第n个散射体簇中第m个散射体的位置，进一步利用几何关系反演求出EAoD和AAoD。

椭圆体模型比圆柱体、半球体模型略微复杂，它将GS散射体分布在一个被截断的椭球体散射区域内，UAV和GS处在椭球体截面的焦点处，记散射区域截断面以下的体积即有效散射区域体积可以表示为V，椭圆体上第n个散射体位置)的概率分布可以表示为

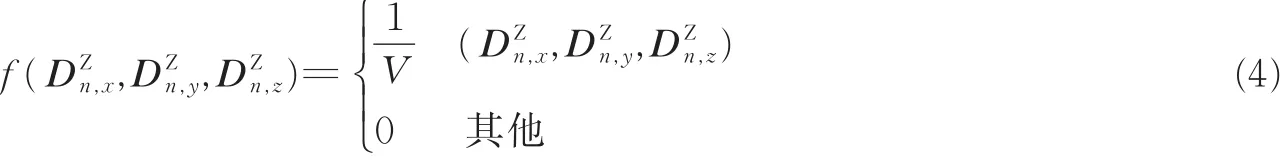
进而利用几何关系推导获得UAV和GS端二维角度参数。

总体而言，不同几何形状的RS-GSCM主要区别在于散射体的位置及统计分布不同，从而导致二维角度参数计算结果的差异性。其中，圆柱体和球体信道模型由于具有几何体的对称性，角度参数可抽象为特定的数学分布，相较椭圆体信道模型的直接推导计算，可大大简化计算量，因而成为当前UAV基于几何随机空地信道建模的主要方法。

表1 信道模型的比较Table 1 Comparison of channel models

2 面向三维轨迹的改进模型及参数计算

2.1 GSCM改进模型

现有GSCM信道模型均假设UAV静止或水平面内做匀速直线运动且忽略了阵列天线位置变化带来的影响，这不符合实际的UAV三维空间任意飞行轨迹的特点。此外，考虑到UAV场景视距路径、地面反射径和其他散射径通常相互独立[21]，本文提出的支持三维任意轨迹和天线阵列的UAV空地信道改进模型，对应各子信道的单位冲击响应可改写为

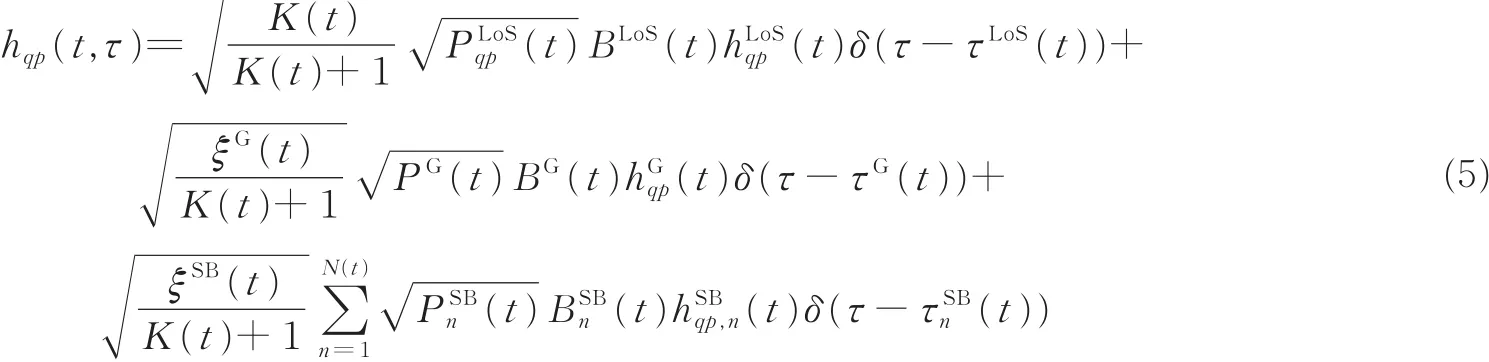
式中：N(t)表示除地面反射外其他一次反射径的数目；PqLpoS(t)，hLqpoS(t)，BLoS(t)和τLoS(t)分别表示视距路径的功率、信道衰落因子、生灭因子和时延别表示地面反射径的功率、信道衰落因子、生灭因子和时延；)分别表示第n条 1次散射径的功率、信道衰落因子、归一化功率、生灭因子和时延。ξG(t)和ξSB(t)分别表示地面反射径分量和1次散射径在分量在总信道功率中占的比例，且

改进后的视距路径衰落可表示为

式中：rtx,q(t)和rrx,p(t)分别用于表示收发三维天线阵元的时变位置矢量，且与初始时刻位置和UAV运动方向有关，即rtx,p(t)=rtx,p(t0)Rtx(t)和rrx,p(t)=rrx,p(t0)Rrx(t)，rtx,q(t0)和rrx,p(t0)分别表示初始时刻收发天线在本地坐标系的位置，Rtx(t)和Rrx(t)分别表示UAV和GS的运动导致的本地坐标系的旋转矢量，可以表示为

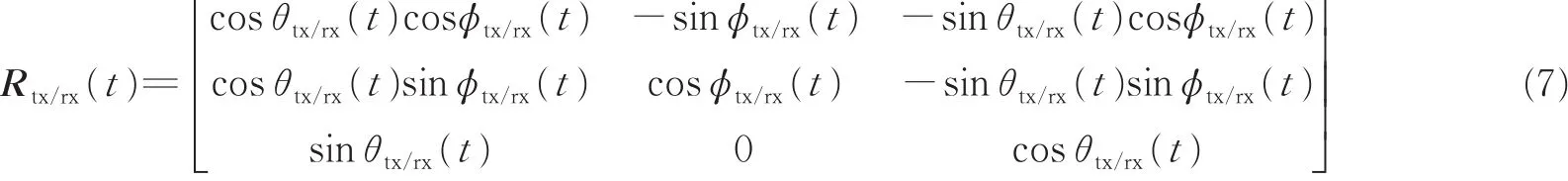
同理，地面反射径和其他反射径的信道衰落因子可以表示为

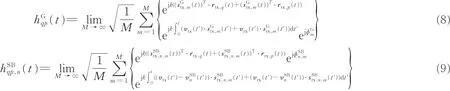
由式(1—3)和式(5—9)可以看出，本文改进模型仍然采用了经典的簇和射线GSCM核心建模思想，但是通过建立UAV和GS两个独立的本地坐标系，并引入空间旋转矩阵和运动角度参数来将UAV和GS的三维运动轨迹和三维天线阵列的影响因素纳入信道模型，从而使得该模型与真实UAV通信场景更为吻合。

2.2 模型参数计算及优化

2.2.1 生灭布尔变量

实测数据表明，由于UAV的大范围快速运动，信道各路径并不是始终存在，而是呈现动态的生灭现象，从而也导致了UAV信道明显的非平稳特性。针对此现象，本文提出的改进模型式(5)采用时变的二状态布尔变量BLoS(t)、BG(t)和BSBn(t)分别描述视距路径、地面反射径和一次散射径的动态随机生灭过程。假设状态0表示消亡，状态1表示存在，则各路径的转移概率矩阵可表示为

式中：λLoS/G/SBD和λLoS/G/SBB分别表示视距路径、地面反射径和1次散射径的消亡概率和新生概率。需要指出的是，不同路径的存活概率即前后两个时间间隔都存在的概率，可以表示为PLoS/G/SBsur(t,Δt)=PLoS/G/SB11(t,Δt)，εLoS/G/SB(t,Δt)表示与UAV和移动端运动相关的信道波动因子，可以表示为

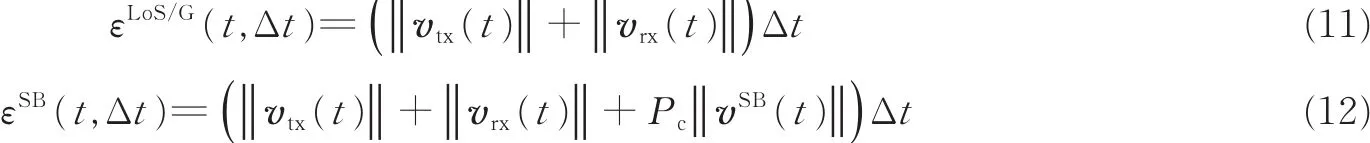
式中：Pc表示所有散射体移动的平均概率；vSB(t)表示散射体的平均运动速度，||vSB(t)||=E{||vSBn(t)||}，其中E{·}表示求数学期望。进一步地，通过设定BLoS(t)，BG(t)和BSBn(t)的初始值，则任意时刻三者的取值可以根据转移概率矩阵动态演进获得。

2.2.2 二维角度参数

UAV和GS通常处于运动状态，UAV，GS和散射体的相对位置也随之动态变化，导致信道模型中二维角度也呈现时变随机性。本文首先令任意时刻UAV和GS地理位置表示为

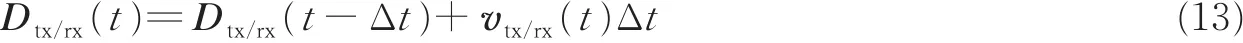
此时，视距路径EAoD，AAoD和EAoA，AAoA可分别表示为

其次，由于极短时间内角度分布近似不变，将各散射支路的随机角度参数建模为上述时变角度均值叠加随机扩展的形式。下面以第n条散射径的第m支路到达角参数计算为例，二者可以分别表示为

和

最后，通过计算第n个散射体第m个散射点的随机位置

进而利用下式分别获得第n条散射径的第m支路对应的离开角度参数为

和

2.2.3 路径时延和功率

UAV信道各路径的传播时延和功率均呈现时变特性，并且时延可以由传播路径的距离表示[4]，利用收发端和散射体的实时位置参数，可以计算视距路径、地面反射径和第n条1次散射径的时延分别表示为

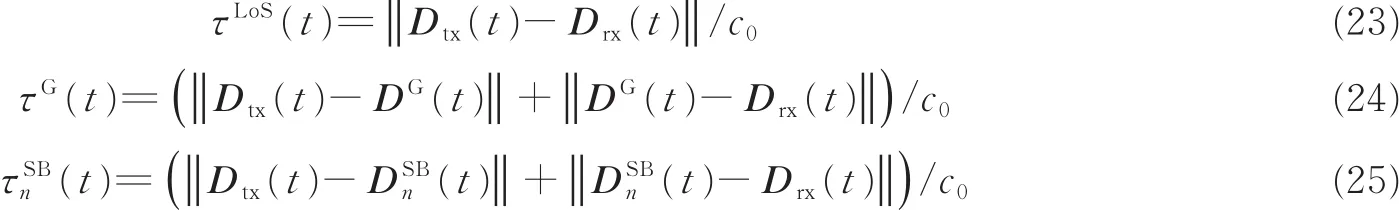
此外，WINNER+标准化模型提供的实测数据表明城市场景下路径功率与时延密切相关，并提供了基于实测数据的路径功率计算方法。考虑到UAV飞行过程中，时延的剧烈变化会导致路径功率快速变化，为了保证各路径输出功率的平滑性，本文视距、反射和第n条散射路径的功率计算分别表示为

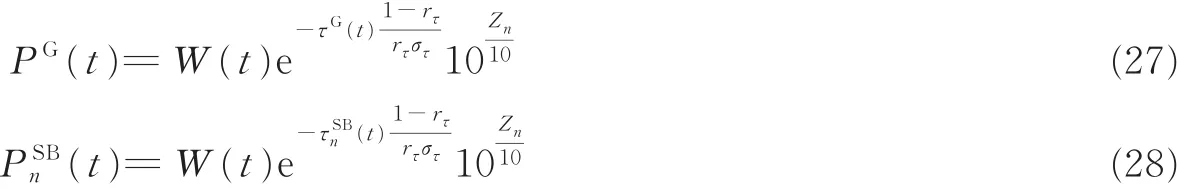
式中：W(t)是为了保证各径功率平滑性引入的低通滤波器函数，Zn表示高斯分布随机变量；rτ和στ分别表示时延分布因子和随机产生的时延扩展。

3 数值仿真及验证

3.1 信道统计特性

信道模型的统计特性对系统性能评估非常关键，也是验证信道模型正确性的有效手段。空时相关特性和多普勒功率谱密度（Doppler power spectrum density,DPSD）是常用的信道二阶统计特性参量。不同天线之间的归一化空时相关系数可以表示为

式中：(·)*表示求函数的复共轭；Hqp(r,f,t)表示信道传递函数且可以通过对信道冲激响应傅里叶变换得到，即

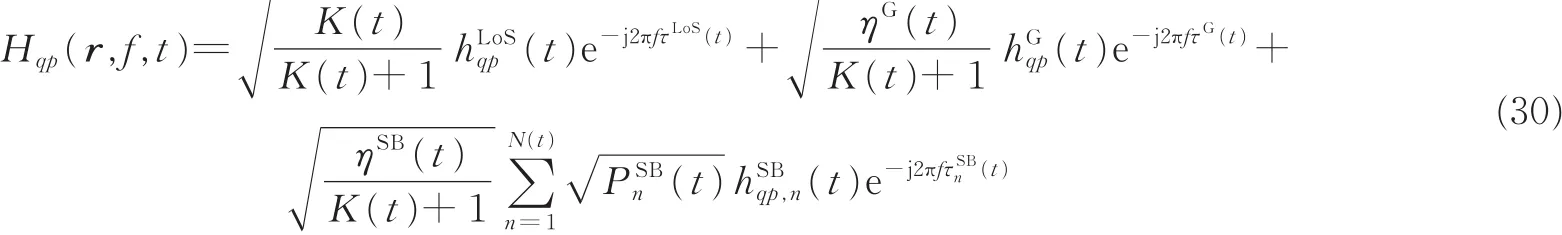
式中：r,f和t分别表示空域、频域和时域的变量；r={Δrtx,Δrrx}为距离间隔，可进一步表示为UAV端和移动端的天线间距进一步地，令q1=q2=q,p1=，可得归一化的时间自相关函数（Autocorrelation function,ACF）表示为

令Δt=0,Δf=0，可得归一化的空间互相关函数（Cross-correlation function,CCF）

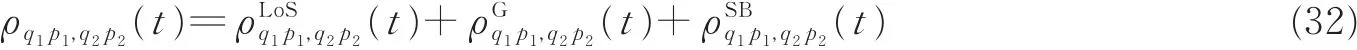
由于三维飞行轨迹场景UAV信道具有非平稳特性，不同于平稳信道的DPSD计算方法，本文通过对ρqp(Δt;t)进行短时傅里叶变换计算获得时变的DPSD，有

式中w(t-τ)表示时间窗函数，实际中窗宽度应小于平稳时间间隔。

3.2 数值仿真结果分析

为验证本文UAV非平稳GSCM改进模型的有效性和准确性，以下利用UAV三维飞行轨迹场景进行仿真验证。考虑到三维飞行轨迹的简化定量描述，假设短时间间隔内UAV和GS的绝对速度和移动方向均服从线性变化，速度参数如表2所示。其他仿真参数如下：载波频率2.4 GHz，散射体移动的平均概率Pc为0.3，UAV与GS的初始间隔为150 m。假设散射体分布的圆柱体半径服从均匀分布R～U(10 m,100 m)，圆柱体的高度则为50 m。接收信号方位角服从VM分布，俯仰角服从Laplacian分布，莱斯因子服从高斯分布K(t)～N(1,3)。

图2(a)仿真给出了无人机三维飞行轨迹场景下ACF的时间演进情况，图2(b)则给出了对应场景CCF的时间演进情况。从图2中可以看出，UAV，GS和散射体的运动引起各自相对位置的动态变化，使得ACF和CCF呈现时变特性。此外，UAV在三维场景下高速飞行时，信道衰落呈现快速起伏的状态，统计特性也迅速变化。进一步，图3给出了由式(29)计算在0，1.5和3 s时刻ACF和CCF的仿真值与理论值的比较情况。由图3可以看出，理论值与仿真值趋于一致。通过数值计算后发现理论值和仿真值的最大误差在0.5%以内，进一步验证了本文改进模型输出统计特性的准确性。

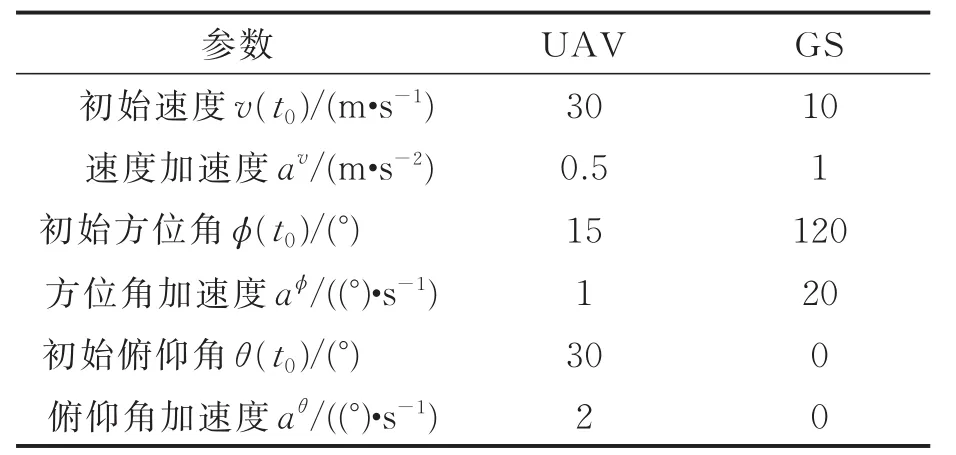
表2 三维运动场景速度参数Table 2 Velocity parameters under 3D trajectory scenarios

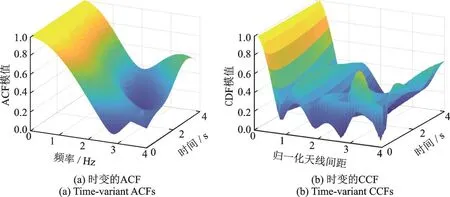
图2 三维轨迹场景下时变ACF和CCFFig.2 Time-variant ACFs and CCFs under 3D trajectory scenarios

图3 三维轨迹场景下不同时刻ACF和CCFFig.3 ACFs and CCFs of different instants under 3D trajectory scenarios

图4 (a)给出了无人机三维飞行轨迹场景下DPSD的时间演进情况，由图可以看出，在该场景下DPSD呈现明显的时变特性。同样地，图4(b)给出了由式(33)计算得出在0，1.5和3 s DPSD的仿真值和理论值的比较情况，从图可以看出，二者结果吻合，最大误差仅为0.14%，进一步验证了改进模型输出统计特性的准确性。

图4 三维轨迹场景下时变DPSDFig.4 Time-variant DPSDs under 3D trajectory scenarios

文献[23]通过实测获得了城市场景下UAV信道的ACF曲线，其假设UAV初始速度为10 m/s，UAV加速度为0.5 m/s2，GS以1.2 m/s匀速前进。本文采用相同的仿真参数，将改进模型输出的ACF随飞行距离的变化结果与实测结果进行比较，如图5所示。由图可以看出，本文模型输出的ACF曲线与实测数据一致，进一步验证了该模型的有效性。

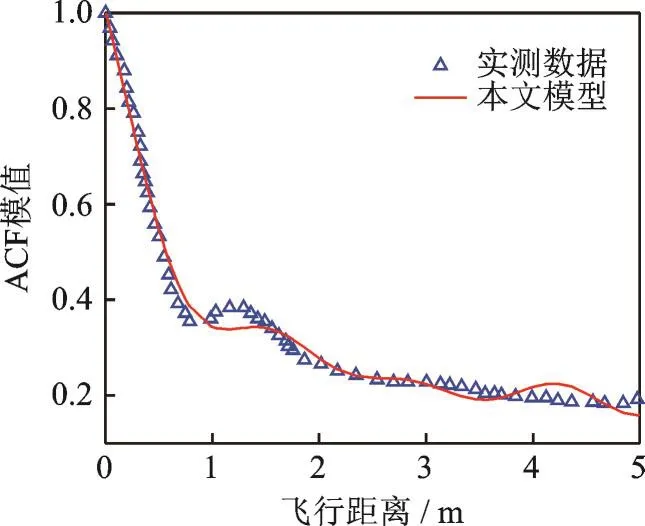
图5 实测结果与仿真值比较Fig.5 Comparison of measured and simulated results

4 结束语

本文提出了一种UAV空地信道改进模型，该模型支持UAV三维飞行轨迹和三维天线阵列，并能够用于描述UAV信道的时变统计特性。仿真结果表明：(1）该模型输出的ACF,CCF和DPSD随UAV和GS的运动变化明显，并且与理论计算结果吻合，能够有效复现UAV信道的非平稳特性；(2）UAV城市飞行场景下ACF实测结果与该模型仿真结果一致，进一步验证了模型的有效性。该模型未来可用于模拟UAV无线通信链路的衰落信道状况，也可应用于辅助优化UAV空地无线通信设备方案设计、性能评估和UAV空中基站部署等领域。