基于矩阵格的BIBD-LDPC码构造方法

李 通，韩建萍，王光耀

（1.山西工程职业学院计算机信息系，太原，030032；2.山西能源学院电气与动力工程系，太原，030600；3.北京工业大学信息与通信工程学院，北京，100124）

引 言

LDPC码在采用置信传播算法译码时，具有逼近香农限的优异译码性能，然而在高信噪比区域的错误平层问题严重地限制了LDPC在某些特殊领域的应用。一般地，陷阱集是造成错误平层的主要原因，而基本陷阱集的危害在所有陷阱集中最为严重。

近年来，针对陷阱集对码字构造的危害，相关研究人员展开了大量的研究。文献[1]提出了采用Tanner图覆盖的方法来消除低密度奇偶校验（Low density parity check,LDPC）码中的陷阱集，错误平层有所改善，不过需要提前得知陷阱集的组合特性。Asvadi等基于环提升思想，通过消除LDPC码中的短环进而避免大部分陷阱集[2]。文献[3,4]以渐进边增长（Progressive edge growth,PEG）算法为基础，在每次添加新边时都会搜索是否会生成基本陷阱集，然而寻找陷阱集任务量过于庞大，虽然至今为止已经有许多高效的搜索算法相继出现[5-10]，仍然造成了计算机资源的浪费。文献[11]基于平衡不完全区组和循环置换矩阵提出一种高围长准循环LDPC码的构造方法，可快速消除陷阱集，然而只适用于特定的码长或码率。

鉴于此，本文摒弃常规的根据Tanner图去除短环的方法，提出以矩阵格为基础的（3，m）QC-LDPC码的无陷阱集构造方案。借助矩阵格中基本陷阱集与斜率之间的关系，将LDPC码的构造转化为在矩阵格中建立新边的问题。仿真结果显示其码字性能好于常规的PEG码，且适用于所有列重大于3的码字。

1 矩阵格构造法

矩阵整数格构造法以平衡不完全区组设计[12]（Balanced incomplete block design，BIBD）为基础。将一个参数为(v,k,λ)的BIBD定义为一个有序对(V,B)，其中V是由v个元素组成的集合，V被分为b个子块，所有的子块构成集合B。分块的原理是：每个子块中有k个点，V中的任意两点确定λ个子块，V中的任意一点存在于r个不同的子块中，故称r为复制数（行重），满足bk=vr，λ(v-1)=r(k-1)。特别地，本文取λ=1，k=3，此时(v,3,1)-BIBD被称为Steiner三重系统。

v=15当 时，令V={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}，B是25个子块的集合。

此时(V,B)就是一个(15,3,1)-BIBD。如果BIBD中若干子块将集合V中的所有点无重复地完全覆盖，则将这些子块的集合称为平行类，如B中的每1列即为一个平行类。相较于去除单个子块，将平行类中的子块全部消除能够构造出更大围长的LDPC码。

定义有序对(V,B)所对应的点块关联矩阵H=(hij)v×b。如果集合V中的第i个元素出现在B的第j个子块中，则hij=1，否则hij=0。(15,3,1)-BIBD对应的奇偶校验监督矩阵H表示为

可以看出H为Gallager码的奇偶校验矩阵，行重为r，列重为k，码率。因为λ=1，所以集合V中的任意两点仅出现在B中的唯一子块内，由BIBD得到的点块关联矩阵H所对应的Tanner中不存在 4环[13]。

定义一个二元矩形整数格L={(x,y)：0≤x≤k-1,0≤y≤m-1}，其中m=v/k=5，整数格内的矩形子集L如图1所示：令lab(x,y)=m·x+y+1表示矩形格L内所有的整数坐标点，称为点标签，所以图1中的整数点依次表示为1～15。点标签在y轴方向是周期循环的，故斜率为1的直线包括三元组 {1,7,13}，{2,8,14}，{3,9,15}，{4,10,11}，{5,6,12}。正好与B中的一个平行类对应，即块B中的第2列，其他斜率的情况依次类推。对于非整数及无穷大斜率的情况本文不作研究，于是斜率s满足：0≤s≤m-1,s∈Z。构造LDPC码的问题可视为在矩形格L指定合适的点集与一系列直线，从而构造出高围长、低错误平层的LDPC码[14-16]。

从点(0,a)出发，每条斜率为s的直线经过3个点，即是3个点的集合{(x,a+x·smodm)：0≤x≤2}，m组直线对应m个斜率，线点关联矩阵对应LDPC码的校验矩阵。定义斜率集Ψ={s1,s2,…,sm}，只要m满足mod((si-sj)·c,m)≠0,∀s1,s2∈Ψ,∀c,i,j∈ [0,m-1]，则矩阵格L中的任意两条直线至多有1个交点，对应Tanner图中的4环被消除。一般地，m为素数，不过即使m为非素数也能够通过选取合适的斜率集构造低错误平层的LDPC码。

2 陷阱集消除

因为基于矩阵格构造的LDPC码不含四环，所以从环长为6的情况开始处理。图 2（a）为一种描述（3，3）陷阱集的“三角状态”，可以产生 6环。3条直线l0，l2，l4对应的斜率分别为s0，s2和s4，相交于点p0，p1和p2。从p2出发到p0共有两条路径：一种是直达；另一种是经过点p1，则点p0的y坐标的两种表达形式分别为(a+2s2modm)和(a+s0+s4modm)，所以所谓的“三角状态”满足

所以只需指定合适的3条直线，使其斜率不满足式（1），就可以避免6环的出现[17]。

（4，4）陷阱集是生成8环的主要原因，其结构共有6种，如图2（b—g）所示，称之为“四边形状态”，此时所构造的正则（3，m）LDPC码的围长为8；图2（h）表示的是矩阵格中（8，0）陷阱集的结构，由一个（4，4）陷阱集（实线所示）经翻转后（虚线所示）形成，此时LDPC码的围长为6或8。为了消除码中的（8，0）陷阱集，同式（1）推导方式类似，所选取的斜率应满足

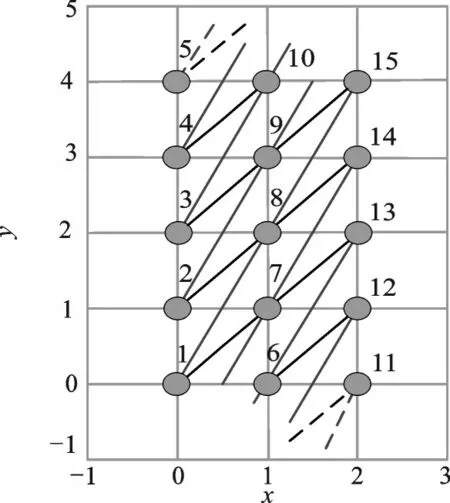
图1 m=5和k=3时的矩阵网格示意图Fig.1 Matrix grid schematic diagram when m=5 and k=3

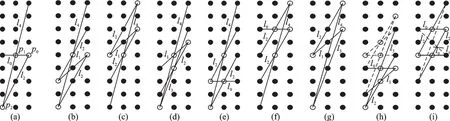
图2 4种陷阱集在矩形格中的表示图Fig.2 Representing graph in rectangle lattice of four trapping sets

与式（1）的推导方式类似，能够消除6种（4，4）陷阱集结构的斜率需分别满足

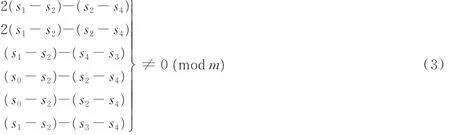
所以只需找到合适的斜率集{s0,s1,s2,s3,s4}满足式（3），便可避免所有（4，4）陷阱集的出现，使所构造的正则（3，m）LDPC码围长至少为10。然而，经过计算发现，为了消除更多的（4，4）陷阱集结构，除了式（3）中的第3个不等式，其他不等式均可同时成立，也就是说图2（d）的这种陷阱集结构无法避免，所构造出的LDPC码围长至多为8。

从文献[15]中可发现，（4，4）陷阱集产生的危害性比较大的陷阱集有（5，3）和（6，4）陷阱集，所以接下来问题可转化为如何消除这两个陷阱集。

如果陷阱集TS2的结构中包含TS1陷阱集，或者说TS2由TS1扩展而来，则称TS1为TS2的父类（TS2为TS1的子类）。为了便于阐述各种陷阱集之间的父子关系，引入了点线表示法。如图3就是由父类（4，4）陷阱集生成的子类（5，3）和（6，4）陷阱集的点线表示图，其中直线代表变量节点，空心圆代表度为“2”的校验节点，实心圆代表度为“1”的校验节点，则一个(α，β){i}陷阱集的点线表示图由α条直线和β个实心圆构成，系数为i。每条直线上有3个圆，表明该变量节点与3个校验节点相邻，即对应的校验矩阵H列重为3。a、b、c分别表示图1中直线x=0，x=1，x=2上校验节点的横坐标，有a≠ b≠ c，a,b,c∈ {0,1,2}，每条线上的a，b，c均不相同。若在度为“1”的校验节点a，b之间连接一条线，则这两个节点的度数变为“2”，为保证校验矩阵H的列重不变，在新线上添加一个度为“1”的校验节点，则（4，4）陷阱集就生成了其子类（5，3）{1}陷阱集，在矩阵格中表示如图2（i）所示。由于添加新线的原则是不能改变原图的围长，而如果连接两个度为“1”的校验节点a或b则会引入6环，围长会从8减小到6，矩阵格中表现为添加的新线斜率为无穷大，仅存在理论研究意义。

令添加的新线lx的斜率为sx，则可推导出避免（5，3）{1}陷阱集应满足

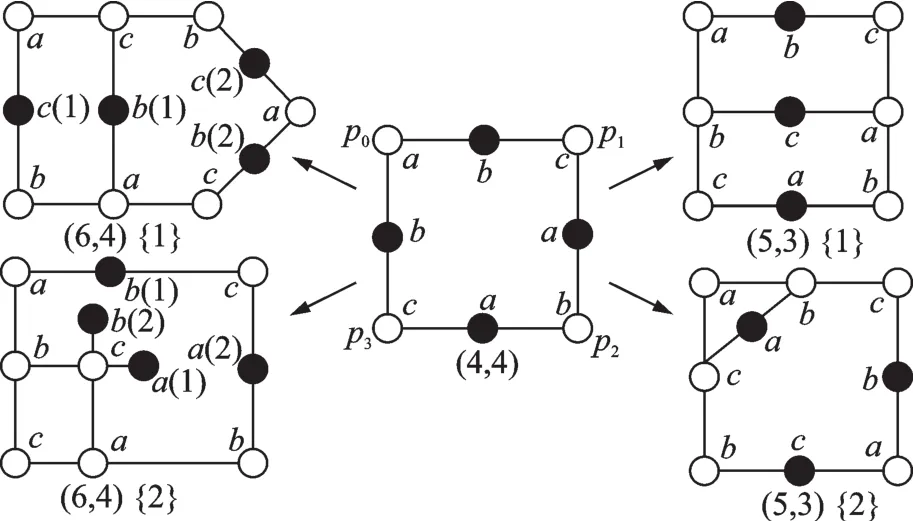
图3 （4，4）陷阱集生成（5，3）与（6，4）陷阱集的点线图表示Fig.3 Line-point graph representation of(4,4)trapping set to(5,3)and(6,4)trapping sets

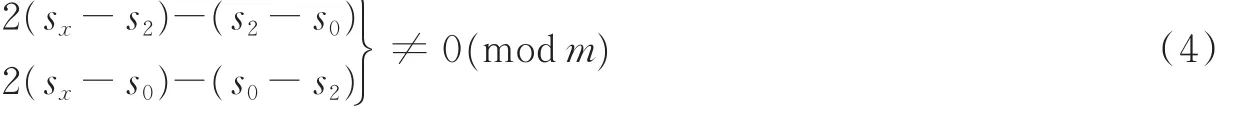
从文献[15]可得，一旦(5,3){1}陷阱集被消除，则其子类陷阱集(6,0)，(6,2){1}和(8,4){1}也随之被消除。同样地，(6,2){1}的两个子类陷阱集(7,1){1}和(8,2){1}也将不会出现，此时所有的（7，3）陷阱集只能由（6，4）陷阱集衍生而来。只要消除了（6，4）陷阱集，则所有的（7，3），（8，0），（8，2）陷阱集也被一并清除，那么图3中的陷阱集基本都可以被避免，极大地提高所构造的正则（3，m）LDPC码的围长，具备优异的错误平层特性。

（6，4）陷阱集的点线表示如图3所示，同（4，4）陷阱集生成（5，3）陷阱集的方法类似，只需在（6，4）陷阱集的点线表示图中添加一条新线便可得到（7，3）陷阱集。对于(6,4){1}陷阱集，由一个8环和两个10环构成。若在两个度为“1”的校验节点b(1)与b(2)之间或c(1)与c(2)之间建立新边，则对应矩阵格中的斜率为无穷大；若在b(1)与c(2)之间或b(2)与c(1)之间建立新边，则生成（8，0）陷阱集；若在b(1)与c(1)之间建立新边，则生成（5，3）陷阱集从而引入更多的子陷阱集；若在b(2)与c(2)之间建立新边，则会生成（3，3）陷阱集，将围长缩小到6，严重影响码字的性能。同样地，对于(6,4){2}陷阱集，由两个8环和一个12环构成。若在两个度为“1”的校验节点a(1)与a(2)之间或b(1)与b(2)之间建立新边，则对应矩阵格中的斜率为无穷大；若在a(1)与b(1)之间或a(2)与b(2)之间建立新边，会衍生出（8，0）陷阱集；若在a(1)与b(2)之间或a(2)与b(1)之间建立新边，会衍生出（3，3）陷阱集，所构造的LDPC码中包含6环。如果在（6，4）陷阱集中添加新边时能够满足上述约束条件，就可以避免出现所有的（7，3）陷阱集，从而消除其衍生的大量陷阱集。

通过分析陷阱集之间的父子结构关系，可以摒弃以往暴力搜索陷阱集的手段，采用高效的陷阱集搜索方案。首先搜索出对码字性能影响最大的陷阱集，然后查找该陷阱集中的度为“1”的校验节点是否在其子图外存在共享的变量节点，若存在，则将变量节点添加至该陷阱集中即可得到一个新的陷阱集；若不存在则继续搜索。

3 算法描述

对于一(v,k,λ)-BIBD中的有序列(V,B)，若集合B中的所有子块能够按照其对应矩形格中斜率分为m个平行类，则称该设计为可分解的，每个平行类称为可分解类。令B(s)为一可分解类，对应于某一斜率s；B'为由一系列可分解类的集合，对应于斜率集Ψ，表示为B'=∪s∈ΨB(s)，Ψ'为不可分解类所对应斜率组成的集合。算法设计的原则是：集合Ψ应含有尽量多的元素s，这直接影响LDPC码的围长，要求围长大于10。

如果直接采用暴力搜索的方式寻找(15,3,1)-BIBD所对应矩阵格中的最大Ψ，整个搜索算法的复杂度为v的指数级，可行性不大。鉴于此，本文提出一种多项式算法来生成最大斜率集Ψ，算法步骤包括斜率的选取、判断、再判断和剔除，确保只有满足式（2，3）约束条件的斜率才能添加进Ψ中。令函数κ(Ψ,m)表示所选取的斜率是否满足上述约束，g(V,B)表示有序对(V,B)对应LDPC的围长，则算法伪代码如下所示。

构造正则（3，m）LDPC码的多项式算法流程

（1）初始化s=0，Ψ ={s}，B'=B(s)，Ψ '={1,2,…，m-1}

（7） B'=B'∪ B(s)

（8） else ifκ(Ψ,m)为真

（9） Ψ=Ψ ∪{s}

（10） Ψ'=Ψ'{s}

（11） elseΨ'=Ψ'{s}

（12） end if

（13） end if

（14）end while

4 复杂度分析

本文多项式算法构造出的BIBD-LDPC码对应的校验矩阵包含|Ψ|×|Ψ|个单位矩阵，每行有m个单位循环子矩阵，每列有k个单位循环子矩阵，每个单位循环子矩阵的内部元素决定其循环移位次数和在校验矩阵中的相对位置。因此，该算法占用的存储量bit，只需存储每个子矩阵的移位次数与相对位置即可。而当LDPC码采用随机构造法时，需要存储校验矩阵中每一个具体元素的值，总体存储空间bit，存储量大大增加。综上所示，本文的优化算法节省了大量的系统存储资源，从而为编译码空留出更多的运行存储空间，提高编译码效率与性能。

5 仿真结果及分析

为了验证本文算法的有效性，选用3种相等码长、码率的PEG[18]构造码进行性能仿真实验并比较。仿真条件为：信号经BPSK调制后在AWGN信道中传输，设置最大译码迭代次数为30次，每个信噪比点的译码帧数为1 000帧，最小错误帧为20帧，译码方案均采用对数域BP算法。为了在保证较小量化损耗的同时改善误码性能，仿真实验均采用中等码率的LDPC码。

码C1为本文算法基于斜率集{0,1,4,9,11}所构造的BIBD-LDPC码，码长为225，码率为0.4；码C2为本文算法基于斜率集{0,1,4,9,11,23}所构造的BIBD-LDPC码，码长为504，码率为0.5。由图4可以看出，码C1、码C2同与之相同码长、码率的PEG码相比，有效地降低了误码率，在高信噪比区域效果更为明显。对于码C1，当SNR≥3.5 dB后，能够稳定获得约0.25 dB的编码增益，这是由于在构造码时消除了（5，3），（6，4），（7，3）和（8，2）陷阱集。对于码 C2，与之对应的 PEG 码在信噪比约为2.5 dB时就表现出明显的错误平层，码C2在整个译码信噪比区域可以得到0.1～0.25 dB编码增益。当SNR=3.5 dB时，误码率由原先的10-5数量级降到了10-6数量级，有效地降低了错误平层。

当k=3，m=53时，搜索出的最大斜率集为{0,1,3,4,9,10,12,13}，由此构造出的码C3,C4的码率均为0.5。在图5（a,b）中，码C3,C4分别与其同码长同码率的Mackay码、Gallager码作性能比较。由图5（a）可得，当1.75 dB≤SNR≤2.25 dB时，码C3可以获得约0.2 dB的编码增益，虽然在高信噪比区域也出现了错误平层现象，但是比Mackay码的错误平层要低；由图5（b）可看出，在SNR≥2.5 dB的中高信噪比区域，码C4能够稳定获得约0.23 dB的编码增益，尤其是在SNR=3.75 dB时，误码率由原先的10-6数量级降到了10-7数量级，误码性能提升了一个数量级。

综上所述，采用本文码字构造算法所构造的列重为3的LDPC码，相较于PEG码、Mackay码与Gallager码，性能有着明显的提升，尤其是在高信噪比区域。

图4 码C1，C2与其对应PEG码的误码性能比较Fig.4 Comparison of error-performance for C1，C2 and its corresponding PEG codes

图5 码C3，C4与其对应LDPC码的误码性能比较Fig.5 Comparison of error-performance for C3，C4 and its corresponding LDPC codes

6 结束语

本文从改进LDPC码的拓扑结构出发，将LDPC码的构造转化为在矩阵格中建立新边的问题。若新边的斜率满足文中的陷阱集约束条件，并且围长不小于10，则将该斜率添加入斜率集。继续添加新边并判断，直至得到一个基数尽可能大的斜率集，以此消除大多数的陷阱集。仿真实验结果表明，本文算法所构造的正则（3，m）LDPC码的围长不小于10，错误平层有所降低，该算法对于列重大于3的校验矩阵依然适用。