认知中继网络中的功率分配算法

唐小岚，杨 科，吴雪雯，朱卫平，吴晓欢

（南京邮电大学通信与信息工程学院，南京，210003）

引 言

众所周知，近几年来我国的无线通信技术得到了迅猛发展，并对国民经济的建设产生了重要的影响[1-2]。在现有的无线通信系统中，除了地面蜂窝网络，卫星通信网与无人机（Unmanned aerial vehicle,UAV）通信网最近也受到了广泛的关注，并成为通信领域的研究热点。虽然卫星通信具有覆盖区域大，通信距离远，通信频段宽等优势[3-5]，但其缺点是造价昂贵、时延较大等;而无人机通信的优势在于机动性好、成本低、维修方便等[6-8]。因此，可以利用无人机通信技术，灵活地建立起一条高效且可靠的数据传输链路。由于无人机在空中飞翔时体积较小，能够用于通信过程的能量有限，所以功率的合理分配[9-10]显得非常重要，为了提高无人机在通信过程中性能的目的，可以通过使用功率分配算法来实现更好、更优的分配。因此文献[11]针对一个认知双向解码转发(Decode-and-forward,DF)中继网络系统，提出了一种功率分配的优化算法，使得在满足次用户总功率约束以及对主用户最大干扰功率约束的前提下，可以最大限度的提高次用户网络的和速率，最后通过拉格朗日对偶法分析，并结合Karush-Kuhn-Tucker(KKT)条件进行求解。但是文献[11]没有考虑将放大转发(Amplify-and-forward,AF)与DF中继协议下的功率分配算法进行比较，分析不够全面。文献[12]先是通过求解系统载波和功率分配的问题，得到了正交频分复用（Orthogonal frequency division multiplexing,OFDM）下行链路系统中权重最大化后的总能效，然后提出了次优和最优的功率分配算法，两个都通过贪婪算法仅仅求解了目标优化问题的下边界。可以看出其功率分配算法是通过迭代算法[13]来求解最优化问题的，由此增加了计算的复杂度，想要求得闭合形式解更是难以实现。

随着无线通信技术迅猛发展，越来越多用户增加了对无线通信网络的服务需求[14-16]。然而频谱资源在无线通信中是有限的，这就使用户需求被大大限制。专家们纷纷提出了很多技术来解决频谱资源利用率这个问题，文献[17]提出了一种具体的集中式频谱分配算法和一种灵活的基于软件定义网络的认知无线电架构，用于提升频谱效率、降低次要用户之间的干扰。但是分配算法较为复杂，虽然提升了效率，但同时也会浪费一些频谱资源。文献[18]提出了两种用于认知无线电网络的协作频谱共享协议，为主要和次要用户的吞吐量提供了更加平衡的解决方案。但此文献仅仅研究了各用户之间的吞吐量平衡问题，未考虑在确保主用户的服务质量下，实现最大化次用户的吞吐量。

在此情况下，为了提升无人机通信的可靠性和频谱效率，首先，在认知无线电的技术下，提出了空时块码（Space-time block code,STBC）的协作中继传输方案。其次，在中继处分别考虑AF和DF两种协议，建立以认知用户传输功率受限和确保主用户的服务质量为约束条件，最大化认知中继网络的吞吐量为目标函数的最优化问题，以求解认知用户的最优功率分配。然后，利用拉格朗日乘子法与KKT条件相结合的方法得到认知用户的最优功率分配及网络的最大吞吐量。最后，仿真结果表明,DF中继协议下认知中继网络的吞吐量优于AF中继协议。

1 系统模型

如图1所示，本文研究的认知无人机通信网由3个认知用户组成，分别为源节点S、中继节点R和目的节点D，每个节点旁都有一对收发信机共享无线信道。为了提高系统的频谱效率，采用了认知无线电技术，最后通过控制发射功率来保证主用户受到认知用户的干扰低于一个门限值。

假设该认知中继网络采用基于STBC的协作中继传输方案，在发射源节点使用空时编码器，将需要发送的信息以空时分组码来发送，此时需要4个时隙来完成源节点与无人机目的节点间的信号传输。具体传输过程如下：第1时隙，源节点S向中继节点R发送数据x1（占用信道1），对使用同频信道1的主用户PU1产生干扰。第2时隙，源节点S和中继节点R分别向无人机目的节点D发送数据x1和x2（分别占用信道2和3），分别对使用同频信道2的主用户PU2和使用同频信道3的主用户PU3产生干扰。第3、4时隙与第1、2时隙的传输过程一样，只是发送数据以空时分组码的形式来发送。第3时隙，源节点S向中继节点R发送数据-。第4时隙，源节点S和中继节点R分别向无人机目的节点D发送数据-和。

图1 认知中继网络的系统模型Fig.1 System model of cognitive relay network

首先第1时隙，源节点S发送信号x1到认知中继节点R，则R接收到的信号为

式中：E1为S发送给R的功率，x1为发送数据字符（E[|x1|2]=1，其中E[·]表示取期望值），hs,r为S到中继R的信道系数，ns,r为均值等于0，方差等于Ns,r的高斯加性白噪声。

第2时隙，源节点S和中继节点R分别发送信号x2和x1到无人机目的节点D，此时中继节点采用AF协议，放大因子为，则无人机目的节点D直接接收到来自源节点S和中继节点R的信号分别为

式中：E2，E3分别为S、R发送给D的功率；hs,d,hr,d分别为S、R到目的地D的信道系数；ns,d为均值等于0，方差等于Ns,r的高斯加性白噪声；nr,d为均值等于0，方差等于Nr,d的高斯加性白噪声。

本文采用Alamouti STBC技术[19],那么第3、4时隙与第1、2时隙是相同的传输过程，只是发送数据不同，则第3时隙，源节点S发送信号-到中继R,接收到的信号为

第4时隙，源节点S和中继节点R分别发送信号x*1和-x*2到无人机目的节点D，无人机目的节点D接收到来自源节点S和中继节点R的信号分别为

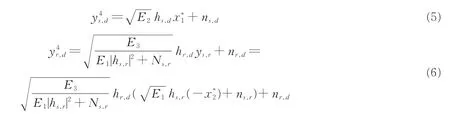
由文献[19]可知，经过STBC译码之后，x1和x2可以被独立地译码出来。无人机目的节点处的端到端信噪比表达式为

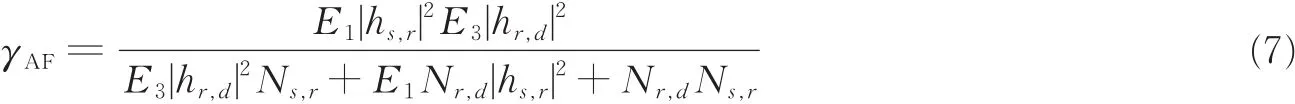
在中继传输系统中，除了AF，通常也会采用DF协议。在DF协议下，中继节点R将接收到的信号ys,r进行解码，得到源信号x1然后转发给无人机目的节点D。跟前面类似，在第2时隙和第4时隙中继R分别发送x1，-给无人机目的节点D，于是，接收到信号分别为

经过STBC译码之后，x1和x2可以被独立地译码出来。最终无人机目的节点处的接收信噪比为

因此，采用DF中继协议下，无人机目的节点处的端到端的信噪比表达式为

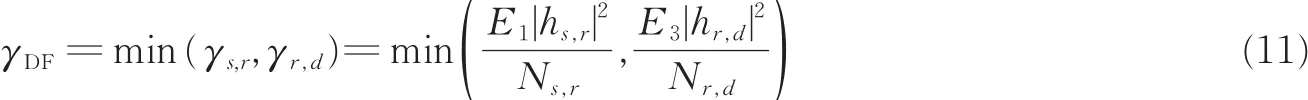
地面城市间发送信号时，由于建筑物较多，导致其路径传输性能相对于地面到空中的传输性能较差，因此源节点S到中继节点R（上行链路）的吞吐量小于中继节点R到目的节点D（下行链路）的吞吐量，即

则式（10）可进一步表示为

在认知中继网络中，认知用户的通信对主用户的干扰必须低于一个门限值，以确保其服务质量满足要求。假设认知用户可获得主用户的瞬时信道增益和可容忍的干扰容限，在第1时隙，源节点向中继节点发送数据（占用信道1），对使用同频信道1的主用户PU1产生的干扰是E1|hspu1|2。在第2时隙，源节点和中继节点向无人机目的节点发送数据（分别占用信道2和3），分别对使用同频信道2的主用户PU2和使用同频信道3的主用户PU3产生的干扰是E2|hspu2|2和E3|hrpu3|2。由于本文采用Alamouti的STBC技术，那么第3、4时隙与第1、2时隙是相同的传输过程，则认知用户的干扰与前面两个时隙相同，因此认知用户的干扰功率限制为

式中：|hrpu3|2为认知中继节点与PU3之间的信道增益；|hspu1|2和|hspu2|2分别为源节点与认知用户PU1、PU2之间的信道增益，其中包含阴影效应以及信道衰落；I1、I2、I3分别为主用户PU1、PU2、PU3能接受的最大干扰功率。

2 功率分配方案

2.1 AF中继协议下的功率分配方案

2.1.1 单节点功率受限

本文提出了在认知用户单节点功率受限以及干扰容限受限的情况下最大化认知中继网络吞吐量的模型。假设认知用户的单节点功率低于一定的值，表示为

式中，Enode为认知用户节点的最大传输功率。则提出的优化认知中继网络吞吐量的模型可以表示为

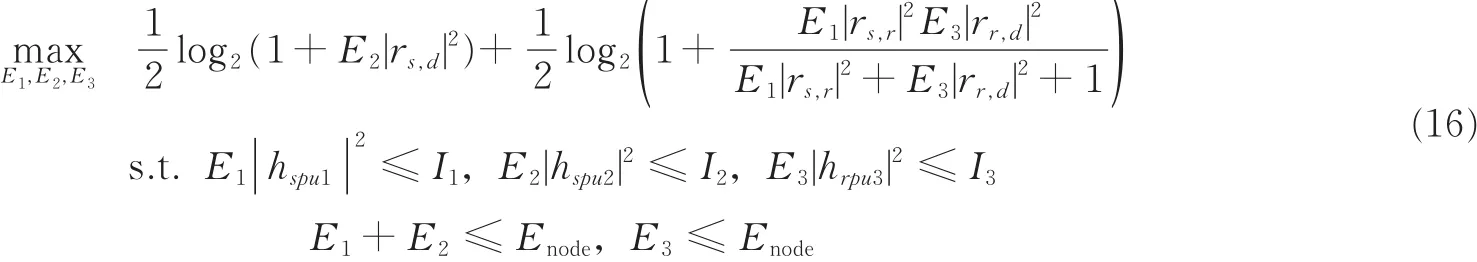
此时，将目标函数由三元降为二元，简化后的优化模型为

显而易见，上述优化问题中的目标函数是凸的，为方便计算，令a=|rs,d|2，b=|rs,r|2，c=|rr,d|2，d=

定理1 为了最大化吞吐量，将拉格朗日乘子法与KKT条件相结合解得最优功率分配方案的闭式解，证明过程如下

由凸优化理论的KKT条件可知

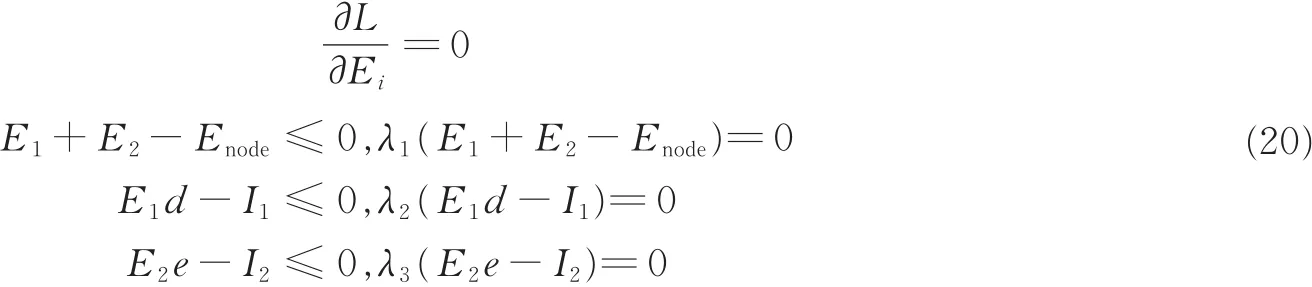
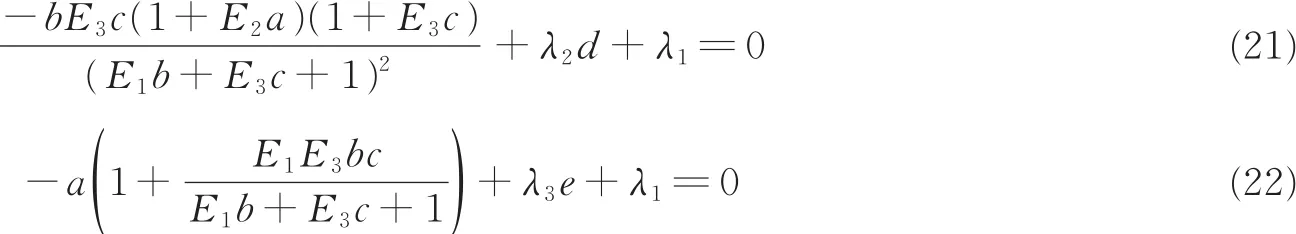
由于拉格朗日乘子λ1≥0，λ2≥ 0，λ3≥ 0，所以分情况进行讨论和求解。

(1)λ1＞ 0，λ2＞ 0，λ3=0

(2)λ1＞ 0，λ2＞ 0，λ3=0

(3)λ1＞ 0，λ2＞ 0，λ3=0

以上3种情况与KKT条件相符。其他不符合要求的情况如下：

(1)当λ1=0且λ2=0或λ3=0时，共3种情况，根据=0可以得到，此时E1=与实际情况中E1＞0,E2＞0不符，故舍去。

(2)当 λ1=0，λ2＞ 0，λ3＞ 0时此时不能满足E+E≤E这个条件，即12nodeE1+E2＞ Enode，故不符，舍去。

(3)当 λ1＞ 0,λ2＞ 0,λ3＞ 0时，，由于参数d,e与瑞利信道系数有关，是变化的，同时Enode也是动态变化的，在仿真过程中无法满足以上条件同时成立，故不符，舍去。

2.1.2 总功率受限

假设认知用户的总功率低于一定的值，表示为

则可以将提出的优化认知中继网络吞吐量的模型表示为

求解过程参考定理1，可得到符合KKT条件的情况：

(1)λ1＞ 0，λ2＞ 0，λ3=0，λ4＞ 0

(2)λ1＞ 0，λ2＞ 0，λ3=0，λ4＞ 0

2.2 DF中继协议下的功率分配方案

2.2.1 单节点功率受限

由于是DF协议，根据前面分析可知，上行链路的吞吐量小于下行链路的吞吐量，即满足式（12），此时认知中继网络的吞吐量为

约束条件满足式（12），（14），（15），所建立认知中继网络吞吐量模型为

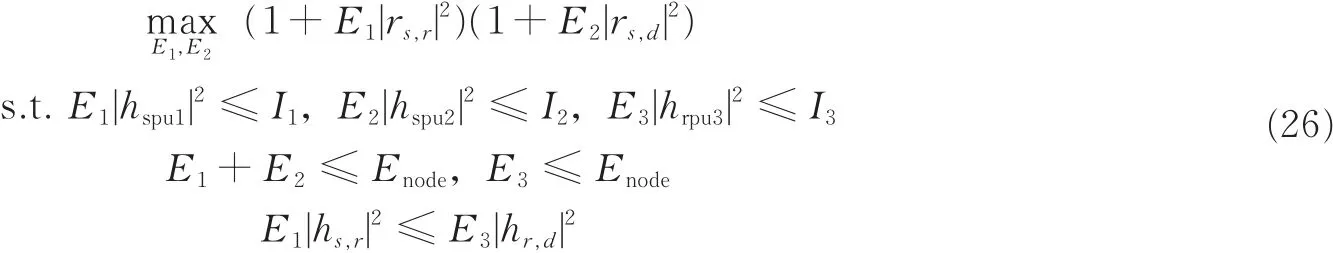
进一步地，可以将式（26）中的E3简化为

由此可得E1简化后为

求解过程参考定理1，可得到符合KKT条件的情况：

(1)λ1＞ 0，λ2=0，λ3＞ 0

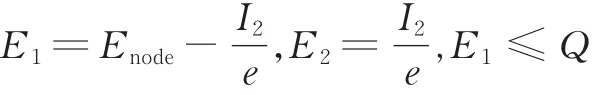
(2)λ1＞ 0，λ2＞ 0，λ3=0

(3)λ1＞ 0，λ2=0，λ3=0

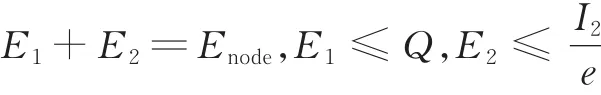
2.2.2 总功率受限

此时约束条件满足式（12），（14），（23），所建立认知中继网络吞吐量模型为

显而易见，式（30）可简化为

求解过程参考定理1，可得到符合KKT条件的情况：

(1)λ1＞ 0，λ2=0，λ3＞ 0

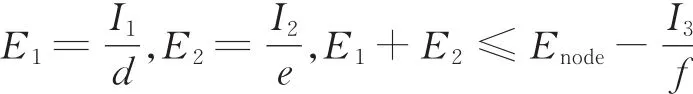
(2)λ1＞ 0，λ2=0，λ3＞ 0

(3)λ1＞ 0，λ2＞ 0，λ3=0

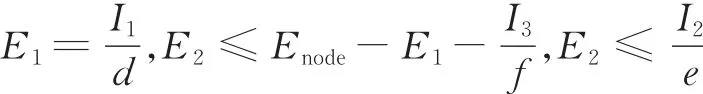
由上述求解过程可以看出，本文首先将非凸优化的问题转化为凸优化问题，然后通过拉格朗日乘子法与KKT条件相结合的方法进行求解。显而易见，KKT条件能保证凸优化情况下求得的解是全局最优解，所以本算法能保证获得的吞吐量是最大的。

3 仿真结果与分析

本节介绍的仿真结果主要是评估功率分配对认知中继网络吞吐量的影响。本文模拟了具有源，目的地和一个中继节点的认知中继网络，比较了4种传输方案：本文提出的具有单节点功率受限的优化方案（Optimal power allocation under single power,OPAS），总功率受限情况下的功率分配方案（Optimal power allocation under total power,OPAT），单节点功率受限情况下的等功率分配方案（Equal power allocation under single power,EPAS），总功率受限情况下的等功率分配方案（Equal power allocation under total power,EPAT），等功率分配（Equal power allocation,EPA）的AF协议与DF协议是传统的中继协作方案，其中所有的节点都使用相同的功率（E1=E2=E3），认知用户的传输功率约束设置为1 W到2 W之间，假定只考虑单位带宽，且信道服从瑞利衰落。

此模型中所有节点之间的距离为100 m，源节点、中继节点和目的节点分别位于（50 m,0 m,0 m),(0 m,0 m,503 m),(-50 m,0 m,0 m)。两个节点之间的信道系数为hi,j～CN(0,1/dv)，其中d是两个节点之间的距离，v=2.5是距离衰减因子。对于本文中的所有仿真，假设所有噪声功率都相等，即Ns,d=Ns,r=Nr,d=1 W。图2，3的仿真中，主用户PU1、PU2、PU3的最大干扰容限为I1=I2=I3=10-3mW。

图2表示在AF中继协议下，不同的功率分配方案下系统吞吐量的仿真结果，显而易见，单节点功率受限情况下的系统性能优于总功率受限情况，这是由于单节点功率受限时的系统总功率相较于总功率受限时的功率更大，从而系统吞吐量更大；最优功率分配方案优于等功率分配方案，且两个方案的系统吞吐量都随着认知用户功率的增加而增加，最后由于受到主用户干扰容限的限制，系统吞吐量会增加到一个饱和状态，则曲线间的距离也越来越小。

图3是在DF中继协议下，4种传输方案对于系统吞吐量的表现情况，可以看出在优化功率分配方案下，单节点功率受限比总功率受限情况下的吞吐量仅提高了0.05 b/(s·Hz)，这是由于DF中继协议中，单节点功率受限与总功率受限的优化问题的约束条件最终都仅与P1,P2有关，但是AF中继协议中，单节点功率受限情况下的约束条件与P1,P2有关，而总功率受限情况下的约束条件不仅与P1,P2有关，还与P3有关，导致单节点功率与总功率受限情况下吞吐量的差异更加明显；最后由于AF在中继节点处放大功率的同时也放大了噪声，导致其系统的性能没有DF中继协议下的系统性能好。

图2 AF协议下不同功率分配的吞吐量Fig.2 Throughput of different power allocations with AF protocol

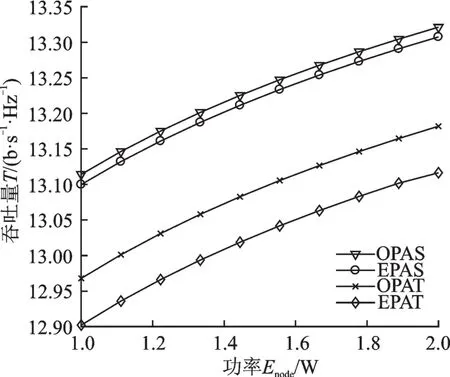
图3 DF协议下不同功率分配的吞吐量Fig.3 Throughput of different power allocations with DF protocol

图4，5分别是在AF和DF中继协议下，不同干扰容限对系统吞吐量的表现情况，且都是在最优功率分配方案下进行比较的。可以看出，当干扰容限增大时，系统吞吐量也随之增大，这是由于干扰容限增大后，对发射功率的约束减小，使得其系统吞吐量增大。

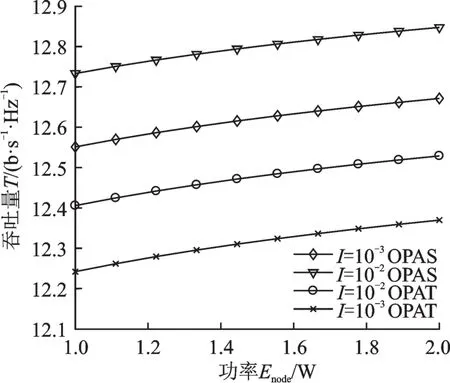
图4 AF协议下不同干扰容限的吞吐量Fig.4 Throughput of different interference tolerances with AF protocol

图5 DF协议下不同干扰容限的吞吐量Fig.5 Throughput of different interference tolerances with DF protocol

4 结束语

本文主要研究了在空时块码的协作中继传输方案下，利用认知无线电技术，对协作中继分别采用AF和DF两种协议进行分析，建立了以认知用户传输功率受限以及主用户干扰容限为约束条件，以最大化认知中继网络的吞吐量为优化问题的系统模型。其中，认知用户的传输功率分别采用了单节点功率受限和总功率受限两种情况，最后，利用拉格朗日乘子法与KKT条件相结合来求解最优功率分配方案的优化问题，仿真结果表明提出的算法优化了认知网络的吞吐量，还进一步显示了DF中继协议下的系统性能优于AF中继协议。