基于分裂法的内部Neumann反散射问题*

张欢，刘立汉

重庆师范大学数学科学学院，重庆 401331

反散射问题是数学物理中一个重要的研究领域，其主要是利用声波或电磁波的散射数据来确定未知散射体的位置、形状及其物理性质。反散射问题的研究成果已在声纳雷达探测、地球物理探测、医学成像、生命科学、遥感技术等其他学科的研究领域中得到广泛应用。在现有的研究中，更多的是考虑入射波和散射波都在散射体的外部，称之为外部反散射问题（见文献［1］），但是正如文献［2-3］中所述，为了解决一些实际问题，内部反散射问题也逐渐得到关注，相比于外部反散射问题，其入射波和散射波都在散射体的内部，且散射波在散射体内部会不断地进行反射，所以内部反散射问题更为复杂。而内部反散射问题是一个非线性不适定问题，为了解决其在求解过程中的困难，目前已有一些解决方法，对于不可穿透散射体，文献［3］通过线性采样法反演在Dirichlet 边界条件下的散射体的位置和形状；文献［4］考虑在Maxwell 方程及其Dirichlet 边界条件下，利用同样的方法反演散射体的位置及其形状；文献［5］将线性采样法延拓到阻尼边界条件的情况，通过该方法反演散射体的位置、形状及其物理性质；文献［6］利用交互间隙法来重构阻抗边界条件下散射体的位置、形状及其物理性质；文献［7］将表示边界值问题的偏微分方程转化为一个等价的非线性积分方程组，并通过正则的Newton迭代法求解这个非线性积分方程组，从而解得散射体的未知边界；文献［8］则将线性采样法进一步延拓到混合边界条件下来重构散射体的位置、形状及其物理性质。对于可穿透散射体，文献［9］利用线性采样法进行数值反演传输边界条件下散射体的位置及其形状；文献［10-11］分别通过分解法和正则的Newton迭代法求解了同样的反散射问题。对于更一般的混合边界条件，文献［12］基于外部传输特征值问题的谱性质分析，证明了可穿透散射体的位置、形状及其物理性质可由腔体内部多个点源的测量数据来唯一确定，再利用线性采样法的想法，构造适应于点源的奇异性的指示函数，进而重构散射体的位置、形状及其物理性质。

本文考虑采用由Kress 和Kirsch 提出的分裂法来求解Neumann 边界的内部反散射问题，这个方法最初是为了解决外部反散射问题。针对内部反散射问题的非线性和不适定性，分裂法将其原问题的这两大难点拆分成两步来解决［2，13］，首先通过测量的数据来构造散射场从而解决原问题的不适定性，然后由边界条件，利用入射波及散射场将原问题转化为一个优化问题，从而达到解决非线性的目的。

1 反散射问题

设D是R2中的一个单连通区域，D的边界∂D具有二阶连续偏导数，波数k> 0，z为散射体D内部的一点。正散射问题是找到散射场us，使得

故矛盾，定理得证。

2 分裂法

假设散射体内部的曲线C上有一个点源z，对∀x∈C，其散射场为us(x，z)，记为usC. 假设Γ 是D外部的一条曲线，定义如下算子

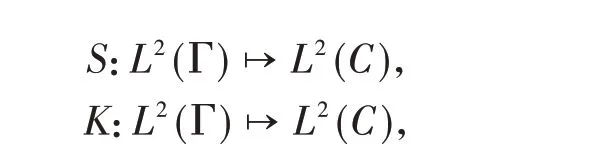
其中

定理2 假设k2> 0 不是-Δ 在Γ 或C内部的Neumann 特征值，则S是紧算子且是单射，此外，S在L2(C)上有稠密值域。

证明 首先证明紧性，因为L2(Γ)为有界集，且L2(C)是有限维的赋范空间，而有限维的赋范空间的任意有界序列都包含一个收敛序列，所以L2(C)是相对紧集，故算子S是紧的。

然后证明S是单射的，设

3 数值例子

本节通过2个数值例子来验证分裂法的可行性和有效性。以下是分裂法求解反散射问题的边界的3个步骤。

第一个例子，考虑重构一个边界为心形线的散射体，结果见图1。第二个例子，考虑重构一个边界为正六边形的散射体，结果见图2。

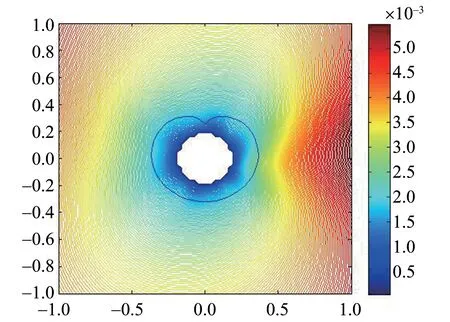
图1 重构边界为心形线Fig.1 Reconstruct a boundary of cardioid