基于软判决的LDPC码校验向量识别算法

罗路为,雷迎科,李 昕,邵 堃

（国防科技大学电子对抗学院，合肥，230037）

引 言

随着通信技术的快速发展，传统的编码方式已经渐渐不适用现代通信的需求，新型编码体制的应用范围已经十分广泛[1]。在各类新型编码方式中，LDPC码因其具有接近香农极限的纠错性能，以及译码简单译码错误可检测等优异性能，十分有利于高速信息传输[2]。因此，各种通信协议和标准广泛采用了LDPC编码。然而，目前大部分算法都是针对LDPC码的闭集识别。LDPC码的闭集识别是指，已知信息发送者所采用的协议，在协议规定的数种LDPC码的集合内，对其编码参数进行识别，待识别的码是该“闭集”中的一个。若是没有或仅有少量这样有先验信息则是开集识别[3]。开集识别是要识别的LDPC码是“无数”中可能性中的一种。然而，LDPC码仅用一个稀疏校验矩阵来定义而且码长较长，致使传统的信道编码识别方法根本不适用于LDPC码的开集识别，该问题成为信道编码识别中的一个难点[4]。

根据已经公开的文献，针对LDPC码的识别技术，国内外已经展开了研究。文献[5]提出了一种LDPC码校验向量的识别方法，该方法依次搜索信道编码预设集合中所有校验矩阵，用伴随式Hamming重量最低的参数组合作为识别结果，但是这种方法需要接收序列中有足够长的无误码序列，因此在噪声环境复杂的识别过程中，该算法的识别性能十分有限，识别效果也不尽人意。文献[6]通过对已识别出的校验向量进行加权，利用已加权的校验向量进行接收序列的迭代译码，重构了(108,3,6)的规则LDPC码。文献[7]提出一种基于后验概率的LDPC码校验矩阵的识别方法，利用后验概率对数似然比均值最大化准则，实现了LDPC码校验矩阵的逆向识别。但是该算法只能对具有准循环结构的校验矩阵进行识别，具有一定的局限性，而且该算法的容错性很差，对信噪比有一定的要求。文献[8]打破传统束缚，提出一种LDPC码稀疏校验矩阵的重建方法。通过对校验向量的行重进行优化，实现了无误码条件下LDPC码校验矩阵的有效重建。然而该方法在误码条件下，对于长码长的LDPC码，算法的识别性能不理想。

针对以上问题，本文利用信道输出的软信息，对信道编码识别方法进行深入研究。结合软判决序列分析法和现有的有限域LDPC码开集识别方法，提出一种利用软判决的LDPC码校验向量的迭代识别算法。

1 校验向量识别的问题描述

图1为本文识别算法所应用的基本通信模型。在发送端，记长度为k的发送信息序列为bi=(bi,1,bi,2,…,bi,k)，i是序列编号，bi中的元素由LDPC码编码器编码后，发送信息序列bi生成码长为n的码字序列ci=(ci,1,ci,2,…,ci,n),ci,j∈GF(2)，j=1,2,…,n。然后对码字序列ci进行调制（在本文中调制方式设为BPSK），最后将调制后的信号si发送至AWGN信道（噪声功率为 σ2）上传输[9]。

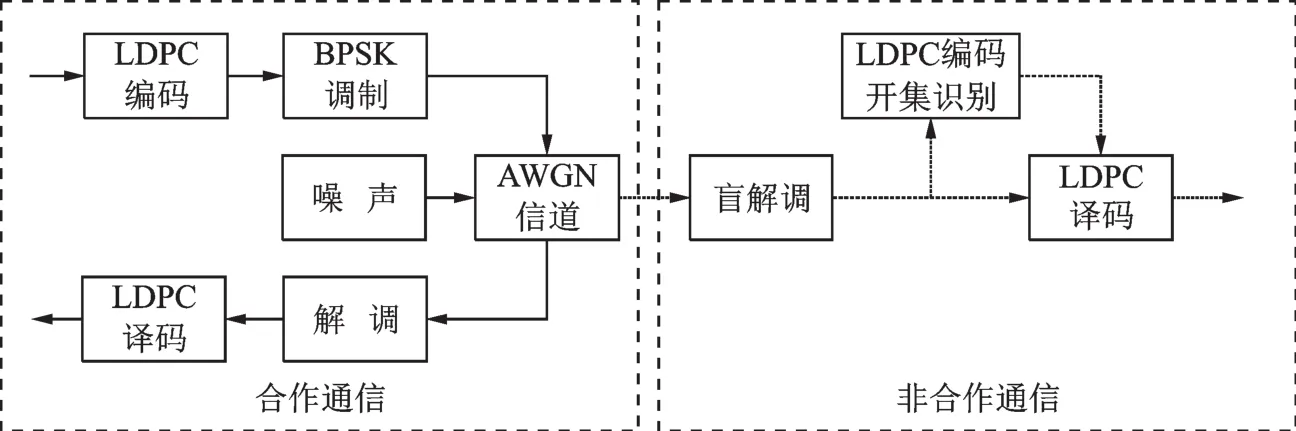
图1 开集识别问题的基本通信模型Fig.1 Basic communication model for open set identification problem

在接收端，首先对接收的信号进行解调，解调方式有两种：硬判决序列记为ai=(ai,1,ai,2,…,ai,n)，软判决序列记为ri=(ri,1,ri,2,…,ri,n)，其中ai,j∈GF(2)，ri,j∈R。本文研究的问题可表述为：利用软判决序列ri对LDPC码的校验向量进行迭代识别，然后由识别出的校验矩阵Ĥ对接收序列ri进行译码，为恢复信息序列b̂i提供先验条件。

通常LDPC码的识别主要包含：码长n，码组起点和校验矩阵。但在实际应用过程中，通常LDPC码的每一帧数据中只有1～2个完整的码字，因此可以通过对帧结构进行分析来获得码组起点和码长n。由于本文主要是针对LDPC码校验矩阵的识别，所以不讨论LDPC码的码长和码组起点。

2 利用软判决的LDPC码校验向量识别算法

2.1 构建校验关系对数似然比

本文为利用软判决接收条件下的校验关系，首先给出后验概率对数似然比(Log-likelihood ratio,LLR)的定义和性质。GF(2)域上的随机变量X和实数域上的随机变量Y，在Y的条件下，定义X的后验对数似然比Lr(X|Y)为

根据Bayes理论，Lr(X|Y)可作如下恒等变换[10]

特别地，当随机变量X等概分布时，Lr(X)=0，此时，Lr(X|Y)=Lr(Y|X)。

由文献[11]可知，LLR函数的部分运算律如下：

两个二维随机变量(X1,Y1)，(X2,Y2)，其独立同分布随机变量X1,X2定义在GF(2)域上，而Y1,Y2定义在实数域上。那么X1⊕X2的后验对数似然比Lr(X1⊕X2|Y1,Y2)为

式中：“⊕”表示GF(2)域上的求和运算；“⊞”为如式（4）所示的定义运算。

由式(4)可以进行多个二维随机变量的推广。对于N个二维随机变量(X1,Y1),(X2,Y2),…,(XN,YN)，有

在式(5)中，双曲正切函数tanh(·)的运算比较复杂，实际应用中通常将式(5)近似为

对GF(2)域上任意一个n维向量xv=(xv,1,xv,2,…,xv,n)T,定义码字ci与xv之间的校验关系为

记LDPC码的校验向量构成空间e⊥。由LDPC码的性质可知，当xv∈e⊥时，对任意码字ci，总有ci·xv=0成立；而当 xv∉ e⊥时，则 ci·xv等概地为“0”或“1”。结合式(1—6),在软判决条件下，可定义式(7)的校验关系对数似然比（Check-relations log-likelihood ratio,CLLR）为

通常情况下，式（8）中的后验概率对数似然比Lr(ci,t|ri,t)未知，可以利用式(2)的结论，展开Lr(ci,t|ri,t)为Lr(ri,t|ci,t)+Lr(ci,t)。因为对于任意信道编码而言，发送比特ci,t为0或1的概率几乎相等，此时Lr(ci,t)=0，则有

图1中，在噪声功率为σ2的AWGN信道模型下，与BPSK调制相对应的似然概率LLR有以下等式成立[12]。

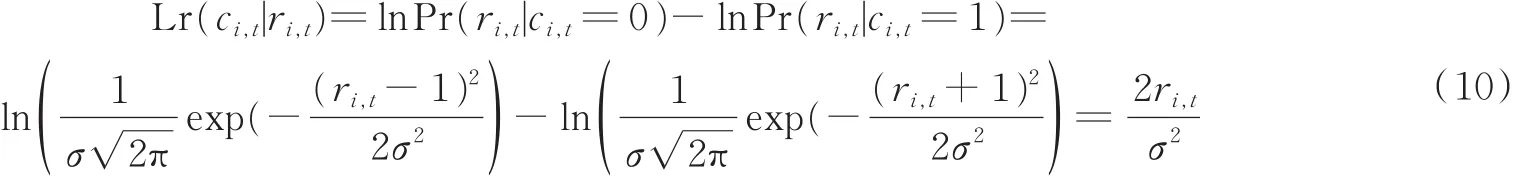
记假设 H0：xv∈ e⊥,H1：xv∉ e⊥。综合式(7,8)可以发现，当 xv∈ e⊥时，有 ci·xv=0成立，与之相对应为正数的概率很大；相反，当xv∉e⊥时，由于码字ci与xv之间不存在约束关系，因而的取值正负不定。

接下来对假设H0,H1进行检验。首先要获取在假设H0,H1下的概率分布。但是在式(8)中定义比较复杂，以至于精确求解概率分布函数特别困难。文献[13]根据编码分析的经验设定的概率分布为正态分布，从其实验结果看，将设为正态分布能够有效地实现对假设H0,H1的检验。本文结合文献[13]的方法，在低信噪比条件下，分析LDPC码时，设定在假设H0,H1下的概率密度函数为正态分布，即有

假设检验后，从一组包含N个码字的接收序列可以得到分布参数的估计值别为

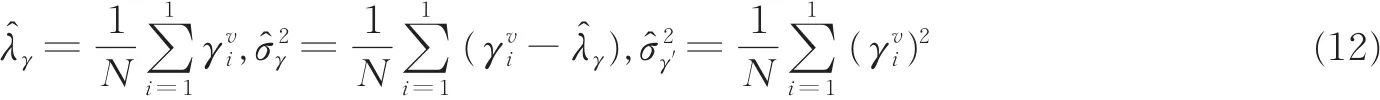
2.2 构建校验向量预搜索空间

通常对于长码长的LDPC码，校验向量的搜索空间极其庞大，运算量也非常大。针对该问题，本文将搜索校验向量的过程巧妙地分为两步：（1）采用文献[5]的方法，寻找最小汉明重量向量，将整个搜索的n维向量空间迅速缩小至一个低维的预搜索空间；（2）采用对偶空间法精细判决预搜索空间中的向量，最后可以得到预期的校验矩阵。

在利用解调软判决接收序列时，为使得在构造预搜索空间时，尽可能降低算法的复杂度，本文结合LDPC码的自身特性，利用软判决序列所提供的可靠度信息，对某些特定的向量进行针对性分析判断[14]。第1步，利用LDPC码校验向量的稀疏特性，把校验向量的搜索范围限定在低重量的向量上。例如在规则LDPC码中，记其校验向量的Hamming重量为P0，则校验向量的搜索区间可固定在Hamming重量为P0的向量上。在非合作通信条件下，若接收方没有关于P0的先验知识，可以设定P0的可能取值集合为Λ={1,2,…,P}，此时校验向量的搜索区间为Hamming重量小于P的n维向量。第2步，利用式(8)中的校验关系，可以根据在H0,H1两种假设下取值的差异，排除不满足校验关系的向量，进而得到较小的预搜索空间Ω。

综上所述，本文利用CLLR的预搜索空间构造算法，通过将可靠的CLLR和LDPC码校验向量的稀疏特性相结合，尽可能地压缩预搜索空间。在低重量的n维空间中，快速剔除非校验向量，获取规模较小的预搜索空间Ω。接下来用规则LDPC码为例，对该方法进行分析说明。

在一组包含较多接收序列的接收数据中，为了迅速提取接收数据的特征，可以构造分析矩阵，记为R'=(r1,r2,…,rB)，分析矩阵R'是从N个接收序列中任意选取B个序列作为样本。令当前识别向量的Hamming重量为p，其中p∈Λ。对于Hamming重量为p的xv对应于R'，根据式(12)，可以得到xv对应于R'的CLLR为

2.3 校验向量的判定

因为在2.2节构造的预搜索空间Ω中，虽然有大量的校验向量，但仍会存在非校验向量，这就需要判定预搜索空间Ω中的向量。记Ω中向量为xw，对应于N个接收序列的CLLR为γω中每个元素相互独立。根据式(11)，可以将γω在两种假设下的概率密度函数定义为[15]

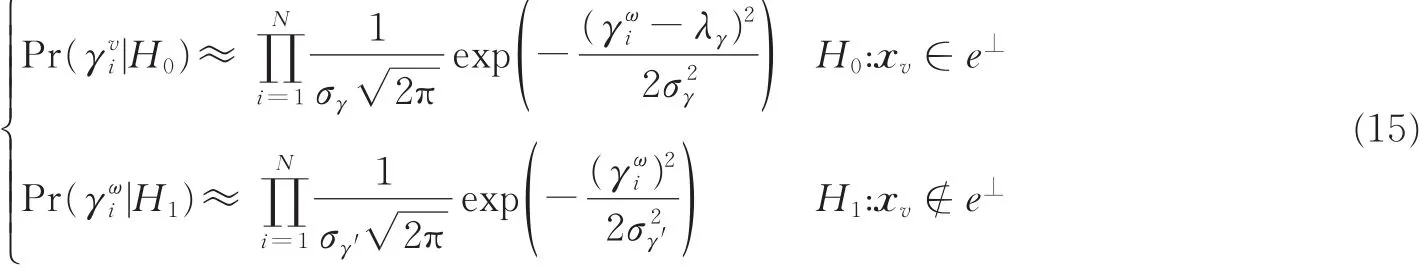
由式(15)，采用广义对数似然比检验，可以实现对预搜索空间Ω中向量的判定。然而广义对数似然检验公式比较复杂，为简化计算，式(15)的等价检验公式为

2.4 校验向量的迭代识别

经过2.2和2.3节的运算后，可以成功地识别出来大部分校验向量，但通常还会漏检少量的校验向量，主要原因有两个方面：（1）在低信噪比环境下，某些判定为可靠的也可能映射出错误的结果，这就会把一些校验向量排除在Ω之外；（2）在判决Ω中的元素时，为了保证识别正确率，通常要求校验向量虚警概率Pf尽可能地小，这会使得校验向量的漏检概率增高。由译码理论可知[16]，校验关系越完整，译码性能越好。为提高算法的译码增益，使得识别的校验矩阵获得较好的译码性能，本文利用多组相互独立的数据进行校验向量的迭代识别，把校验向量搜索算法和译码迭代算法的结果相互不断地更替，使校验矩阵Ĥ更加完善。

图2为校验向量迭代识别算法的结构框图，首先将接收数据切分为多个矩阵R，R由N个接收序列组成，进行参数初始化。在第d次迭代时，输入的接收矩阵记为软判决接收矩阵识别出的校验矩阵。然后对进入系统的Rd进行SISO译码，提高译码后矩阵的可靠性。然后，采用2.2节和2.3节的算法求出与相对应的校验矩阵。最后结合新识别出的对之前识别出的参数P,d进行更新。

图2 校验向量迭代识别算法的结构框图Fig.2 Structural block diagram of iterative verification algorithm for check vectors

2.5 算法步骤

综上所述，本文算法步骤如下：

（1）构建软判决接收矩阵R1,R2,…，对参数进行初始化P=1,d=1,

（3）由2.2节和2.3节，求解Hd；

（4）根据2.4节的分析，利用Hd与～H，判断迭代停止的条件。如果不满足停止条件，则更新参数～H和p，输入新的分组数据Rd+1，然后返回（1）；如果满足停止条件，则输出校验矩阵Ĥ，并利用Ĥ对接收序列ri进行软判决译码，最终恢复出信息序b̂i。

3 实验结果及其分析

为验证本文校验向量识别算法的性能，对其进行仿真实验。实验采用IEEE 802.11n标准中(648，324)，(1296,648)LDPC码，对算法进行100次蒙特卡洛实验。从预搜索空间Ω的数量、迭代次数对校验向量识别数量的影响以及算法的整体识别性能3方面进行实验。在仿真过程中，每一个软判决接收矩阵Rd中包含的接收序列数N=100，由校验矩阵～H对Rd进行SISO译码，校验向量迭代识别的最大无更新次数TH=5。译码迭代次数为30次。

3.1 预搜索空间Ω的数量分析

2.2 节的理论分析表明：通过构造预搜索空间Ω，可以大幅度降低校验向量的搜索空间，减少算法的运算量。对实验过程中预搜索空间Ω的数量进行了统计，表1和表2分别给出了两种LDPC码在不同误码率条件下，预搜索空间Ω中平均包含的校验向量数，以及最后识别出的平均校验向量数。

表1 （648，324）LDPC码的识别结果Table 1 Recognition result of（648，324）LDPC

表2 （1296，648）LDPC码的识别结果Table 2 Recognition result of（1296，648）LDPC

从实验结果可知：随着误码率的增大，需要的校验向量数目也逐渐增大。如果不构建预搜索空间，这个数目将成指数级增长，这说明了构建预搜索空间的必要性。从表2可以看出，即使是针对(1944,872)LDPC的识别，通过在预搜索过程中筛除非校验向量，使得在搜索校验向量时，搜索空间的规模都能够控制在105以内，校验向量的搜索范围得到了大幅度降低。

3.2 迭代次数对校验向量识别数量的分析

为分析迭代次数对校验向量识别数目的影响，对(648，324)LDPC码进行不同次数的迭代，统计识别出的校验向量数目的变化情况。图3给出了校验向量搜索迭代次数在d=5,10,15这3种情况下，本文算法识别出的校验向量数目随误码率的变化情况。

从图3可知，随着误码率的不断增大，一次迭代识别出的校验向量数目逐渐减小。但是通过增大迭代次数，在相同误码率条件下，获得的有效校验向量数目逐渐增多，每增加5次迭代，平均多识别的校验向量数目约100个。即使在误码率为0.07的条件下，15次迭代后，本文算法识别的线性无关校验向量的平均数目可达302.3个（在(648，324)LDPC码中线性无关校验向量有324个），识别率达到93%。由此可见，增加迭代次数有利于获得更多的有效校验向量数，以及增强算法的抗误码性能。

3.3 算法的识别率性能分析

为分析本文算法的识别率性能，对本文算法与文献[5]算法识别率性能进行比较。针对IEEE 802.11n标准中3种不同的LDPC码，进行实验分析。图4给出了在相同条件下，本文算法与文献[5]算法的识别率随误码率的变化曲线，其中识别率是指正确识别的校验向量数目与真实的校验向量数目的比值。

图3 迭代次数d=5,10,15条件下识别出的校验向量数Fig.3 Number of check vectors identified when d=5,10,15

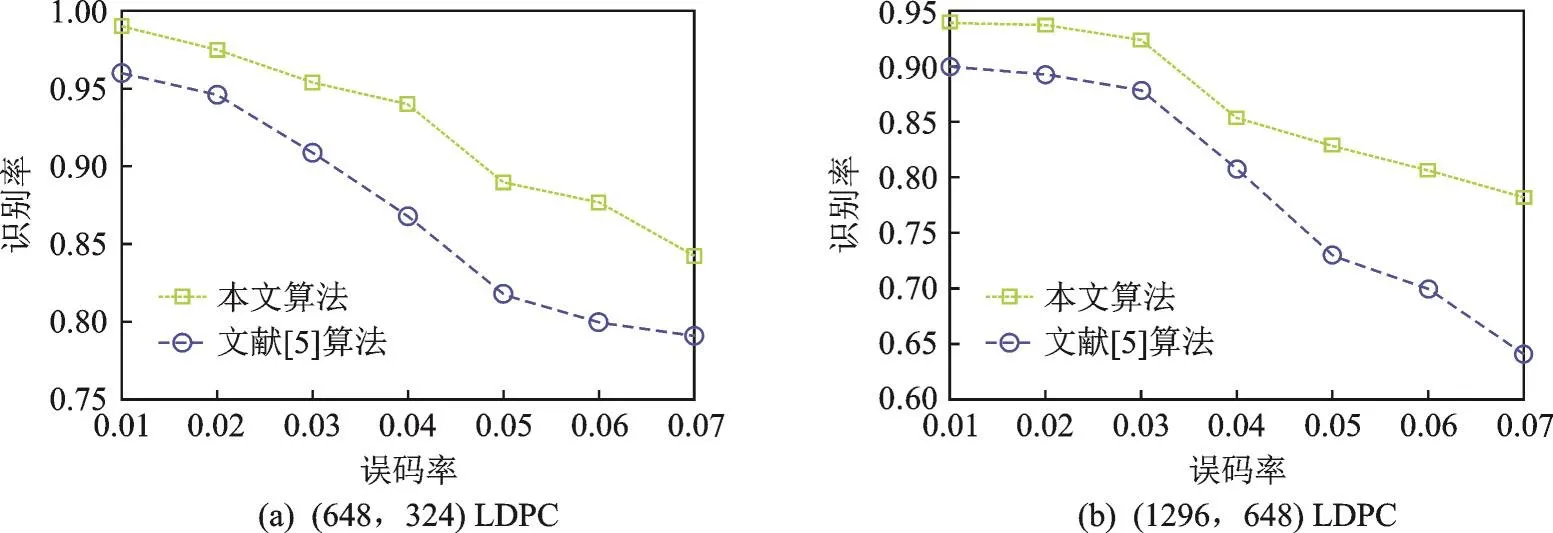
图4 本文算法与文献[5]算法的识别率对比Fig.4 Comparison of the recognition rate between the proposed algorithm and algorithm in Ref.[5]

从实验结果可知，针对IEEE 802.11n标准中两种不同的LDPC码，本文算法的识别率整体都大于文献[5]算法的识别率，平均识别率提高约15%。而且，在不同的误码率条件下，本文算法识别率都高于文献[5]算法的识别率。当误码率大于0.03时，本文算法针对两种不同的LDPC码的识别率都能达到90%以上。

为进一步验证本文算法的识别性能，利用识别出的校验向量进行译码分析。为统一实验条件，仿真时统一迭代次数d=15。采用常规的最小和BP译码算法进行译码。图5给出了本文算法与文献[5]算法的译码增益性能比较。

从图5可以看出，随着信噪比的上升，误码率逐渐减小，而且本文算法的译码增益整体上优于于文献[5]算法。在b̂i误码率为10-3时，相对于文献[5]的算法，本文算法的信噪比增益约为2.3 dB。

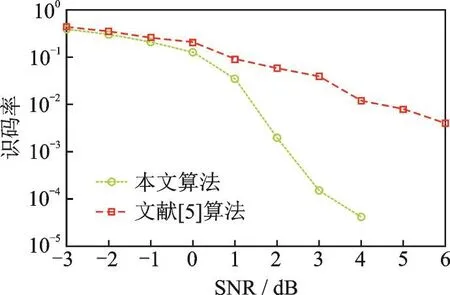
图5 本文算法与文献[5]算法译码增益的比较Fig.5 Comparison of decoding gain between the proposedalgorithmandalgorithminRef.[5]

4 结束语

针对现有LDPC码校验向量识别算法容错性差和识别率低的问题，从软判决的角度出发，提出一种LDPC码校验向量迭代识别算法。通过本算法，构造的向量搜索空间得以大幅度降低。算法利用多组相互独立的数据进行校验向量的迭代识别，通过校验向量搜索算法和译码迭代算法之间的相互更替，使校验矩阵得以进一步完善。仿真结果表明，与已有算法相比，本文算法的向量搜索空间大幅度降低，识别率明显提高，而且算法获得的译码增益提高约2.3 dB。