基于核岭回归方法的定位算法研究

汤 卓，乐燕芬，施伟斌

（上海理工大学光电信息与计算机工程学院，上海，200093）

引 言

无线传感器网络技术随着电子和通信技术迅猛发展而出现，并在过去几年成为广受关注的研究领域。无线传感器网络(Wireless sensor network，WSN)由大量的微型自主传感器组成，每个传感器都具有感知、处理和传输环境信息的能力[1]。传感器的定位是无线传感器网络环境中的一个基本问题，因为很多收集到的传感数据只有与位置相结合才有意义。最直接的解决方法是为每个传感器配备一个定位设备，如全球定位系统(Global position system,GPS)。然而GPS设备功耗大、成本高，且由于GPS信号衰减而在室内环境下应用受限，这都使得用GPS进行传感器的定位不太现实。更好的解决方法是用相对定位，其中设置了两种类型的传感器节点：已知位置且固定的锚节点，未知具体位置需要根据锚节点提供的信息去定位的盲节点。

目前基于WSN的定位算法分为两类：一类是利用距离信息去估计目标位置的算法，如到达时间法(Time of arrival,TOA)[2]、到达时间差法(Time difference of arrival,TDOA)[3]、到达角度法(Angle of arrival,AOA)[4]等。另一类是位置指纹定位法，位置指纹定位法一般采用接收信号强度指示(Received signal strength indicator，RSSI)作为特征来描述物理位置，离线阶段收集所有离线位置点接收到来自各锚节点的RSSI，建立指纹数据库。在线匹配阶段，通过盲节点接收到的RSSI，按照一定的匹配算法与指纹数据库进行匹配，从而推断出盲节点的位置。相比于第1类算法，位置指纹法不需要添加额外的硬件设备来获取角度信息或者距离信息，使其成为最近几年定位应用的研究热点。目前常用的有 K 近邻算法(K-nearest neighbor，KNN)[5]，加权 K 近邻算法(Weight K-nearest neighbor，WKNN)[6]，这两种算法的计算复杂度较小，但由于室内复杂的物理环境，RSSI具有空间变换性和时间变化性，这使得RSSI信号与位置之间并没有确定不变的关系，利用这类方法，会存在较大的定位误差。而针对高精度的定位需求，Horus系统首先实现了基于概率的定位解决方案[7]。利用贝叶斯法，通过计算待定位点的后验概率估计该点的物理目标[8]。文献[9]针对贝叶斯算法存在后验概率可能为0以及计算量较大的问题，提出了一种改进的算法。Fang等[10]采用主特征提取(Principal component analysis，PCA)方法，提取指纹数据之间的线性特征，减小环境变化带来的RSSI波动，但这种方法忽略了数据间的非线性关系。李华亮等[11]在此基础上引入了核函数，将原始位置指纹空间映射到更高维的样本空间，更大程度地利用了位置指纹数据。此外还有文献[12]提出了基于最小二乘支持向量机(Least square-support vector machine,LS-SVM)的位置指纹定位算法，将定位问题转化成一个多类别分类问题，以降低计算复杂度和提高定位精度。

不同于上述方法，本文提出了一种基于核岭回归(Kernel ridge regression,KRR)的定位算法。该算法在离线阶段利用核岭回归方法训练得到定位模型，获得RSSI信号向量与物理位置之间的映射关系；在线阶段，通过盲节点收集的RSSI测量值，利用定位模型估计盲节点的物理位置。通过本文算法使用的RSSI数据来自于真实的环境，实验表明本文提出的算法比常用的WKNN算法精度更高。

1 基于核岭回归的定位算法

1.1 定位算法流程图

整个定位过程如图1所示，分为离线训练阶段和在线匹配阶段。离线阶段通过KRR方法得到RSSI信号与物理位置之间的映射关系，建立定位模型用于在线匹配阶段;在线采集目标点的RSSI值，利用定位模型估计出当前所在位置。

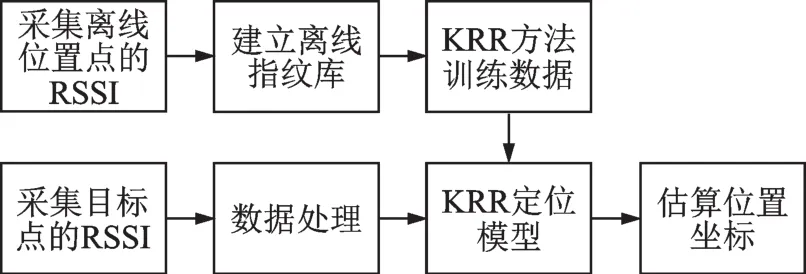
图1 定位流程图Fig.1 Location flow chart

1.2 核岭回归算法的提出

回归分析方法是利用数理统计方法分析数据，建立自变量和因变量间的回归模型，用于预测因变量变化的分析方法[13]，其中比较经典的是Hoerl和Kennard提出的岭回归算法[14]。岭回归算法是在最小二乘法的基础上引入了正则项，使回归模型具有较好泛化能力和稳定性，但是岭回归算法并不能处理自变量间非线性相关的情况[15]。KRR算法是在岭回归算法基础上引入了核方法，通过核函数将自变量空间映射到高维特征空间，然后用岭回归方法在高维特征空间中分析和处理数据[16]。由于RSSI数据间存在着非线性关系，本文采用KRR方法先将原始RSSI指纹空间转换到高维空间中，再建立RSSI信号与物理位置的映射关系。

1.3 核岭回归算法的描述

1.3.1 离线指纹库建立

本文提出的方法主要针对2维环境下目标位置的估计。使用两种类型的节点：锚节点和盲节点。锚节点是已知具体位置的节点，用ai,i∈{1,…,Ns}表示，盲节点是待定位的节点。在离线配置阶段，把Np个确定的离线位置点，其位置用pl,l∈{1,…,Np}表示，均匀分布在监测区域中，锚节点以固定的初始功率向周围环境发送信息广播，在离线位置检测信号并获得RSSI值，用ρl=(ρ1,l,…,ρNs,l)T表示在离线位置点pl上接收到所有锚节点的RSSI信号，把ρl与pl一一对应起来，一共有Np对（ρl，pl），构成离线位置指纹库。

1.3.2 非线性回归模型的建立

利用离线阶段的指纹库，训练模型函数φ：RNs→R2，该函数的输入为RSSI测量值，输出为目标的物理位置。为了确定上述函数 φ（·），把 φ（·）按着维度分为是一个Np×2的矩阵，其中pNp为参考节点的位置，P*,d为P矩阵中的d列，Pl,*为P矩阵中的l行。对于每一个φd（·），φd：RNa→R,d∈{1,2}，采用岭回归方法，其目标代价函数表达式为

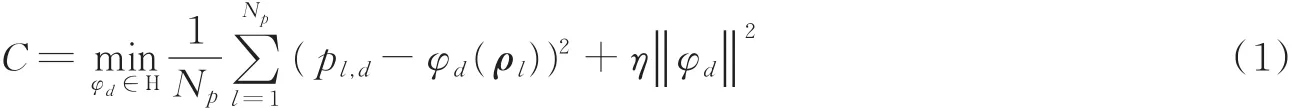
式中：η是正则化参数，控制训练误差与计算复杂度之间的平衡表示L2范数。由于岭回归属于线性回归，而RSSI测量值与物理位置之间存在着非线性关系，因此引入核方法，根据文献[17]，最优函数可以写成

式中：k：IRNs× IRNs→IR是一个再生核函数，αl,d是模型的参数，α*,d表示第d列的所有元素，αl,*表示第l行的所有元素。把式（2）代入式（1）中，得到对于α*,d的双重优化问题，对其求导使之等于0，求出 α*,d，如

把式（4）代入式（2），求出函数

核函数中综合准确率、召回率、F测量和信息增益等多种评估准则，发现径向基函数在各种准则中总体最优[18]。本文采用径向基函数中最常用的高斯核函数，σ表示核函数的带宽，它与正则化参数η一起控制着函数的平滑度、噪声容忍度和泛化程度，表达式为

2 仿真与实验结果分析

2.1 基于MATLAB的算法仿真

考虑一个100 m×100 m的监测区域，生成18个锚节点和100个离线位置，让锚节点均匀分布在监测区域的两边，每侧为9个锚节点，离线位置均匀分布在监测区域中，每隔10 m取一个离线点。常用的无线信号传输模型有自由空间模型、对数距离路径损耗模型和Okumura-Hata模型等，由于节点性能的分散性和环境的复杂性，使用自由空间模型误差会较大[19]，由于KRR算法是基于非测距的定位算法，因此不采用对数距离路径损耗模型，Okumura-Hata模型是通过分析统计大量观测数据得出的经验公式，文献[20-21]等在仿真阶段都利用了该模型产生所需要的RSSI值，Okumura-Hata模型公式为

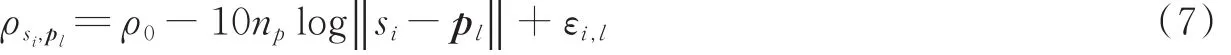
式中：ρsi,pl是在离线位置点pl接收到来自锚节点si的信号强度，它是ρl矢量的第i个元素。ρ0是初始信号功率，设为-10 dBm，np是路径损耗指数，在很多文献中通常设置为4，‖ ‖si-pl表示锚节点与离线位置的欧氏距离，εi,l是影响RSSI值的噪声，用σρ表示噪声的标准差，离线采集时设置为1 dBm，高斯核函数带宽取4，正则化参数η=5.0×10-9。对每一个离线位置，结合其与锚节点的欧氏距离，利用式（7）计算得到相应的RSSI值，建立离线指纹库。

然后考虑在线目标定位问题。为此生成一个轨迹，随机提取轨迹中的100个点作为目标点，使用相同的模型计算目标节点接收到的RSSI值。由于无噪声设置在实际环境中是不现实的，噪声存在于所有场景中，为此增加一个零均值，标准差σρ=2 dBm的高斯白噪声，实验采用平均定位误差作为定位标准。图2(a)为实际轨迹和使用KRR，KNN，WKNN算法定位获得的轨迹，图2(b)为3种算法在每一个目标点的定位误差分布图，计算3种算法的平均定位误差：KNN算法为4.27 m，WKNN算法为3.79 m，而KRR算法为2.48 m。

(1)锚节点数量对算法性能的影响

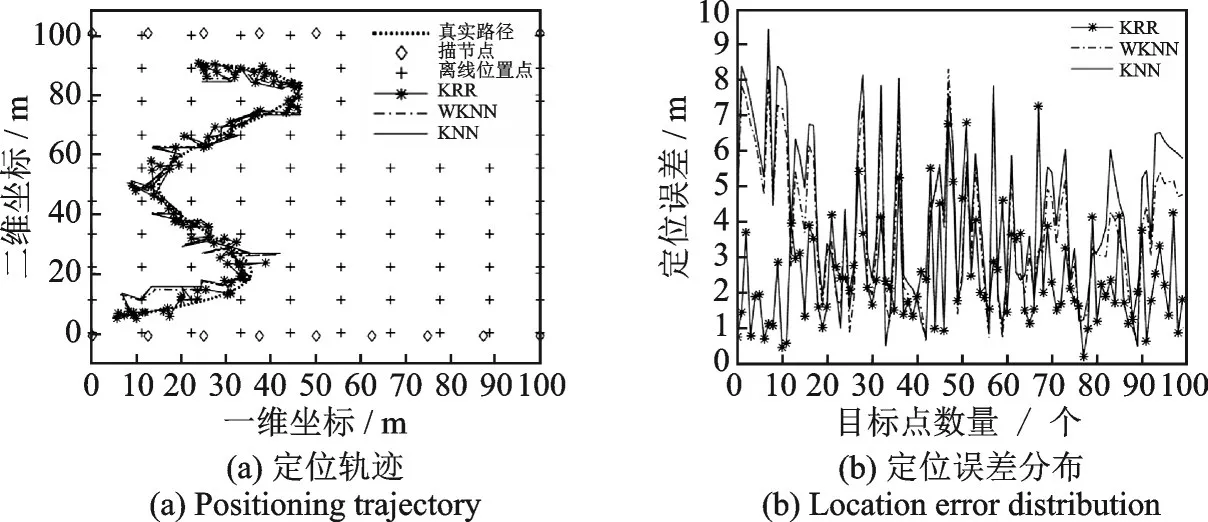
图2 目标节点的定位及误差分布Fig.2 Location and error distribution of target nodes

在位置指纹定位算法中，锚节点数量是影响定位性能的一个重要的因素。为了研究锚节点数量对定位精度的影响，仿真过程中设置Np=100，离线采集时σρ=1 dBm，在线匹配时σρ=2 dBm，锚节点数量取4～40的整数。从图3可以发现，在一定范围内，平均定位误差随着锚节点数量的增加而减少，当锚节点数量为28时，平均定位误差达到最小值，为2.39 m。但随着锚节点数量的继续增加，平均定位误差并未有明显减小，这也说明定位中布置适量的锚节点能达到理想的定位精度，过多的锚节点可能引入RSSI信息的冗余，并不能达到预期的精度提高。

(2)网格密度大小对算法性能的影响

在位置指纹定位算法中，网格密度也是影响定位性能的一个重要的因素，在100 m×100 m的监测区域中，通过改变离线位置点的数量来改变网格密度。在仿真过程中设置锚节点数量不变，Ns=28，离线采集时σρ=1 dBm，在线匹配时σρ=2 dBm，离线位置数量取62,…,252，图4为采用KRR算法的平均定位误差图。从图4可以发现，当离线位置数量为64的时候，平均定位误差为3.47 m，当离线位置数量为121的时候，平均定位误差为2.27 m，当离线位置数量为400的时候，平均定位误差为2.24 m，说明在一定范围内，离线位置数量的增加能更精确地估计出目标点的位置，但超出范围之外，随着离线位置数量的增加，平均定位误差趋于稳定。

(3)标准差σρ对算法性能的影响

任何环境下都有一定程度的噪声，为了研究不同程度的噪声在KRR算法下对定位精度的影响，在仿真过程中设置Np=100，Ns=28，噪声标准差离线采集时σρ=1 dBm，在线匹配时σρ取0～5 dBm，图5为不同σρ下的平均定位误差图。从图5可以发现，σρ逐渐增大，定位误差也随之增大，当σρ=4.5 dBm时，平均定位误差为8.49 m。

图3 锚节点数量变化的平均定位误差分布Fig.3 Average positioning error distribution of number of anchor nodes changes

图4 离线位置数量变化的平均定位误差分布Fig.4 Average positioning error distribution of number of off-line positions

图5 噪声标准差σρ变化下的平均定位误差分布Fig.5 Average value of location error distribution with sigma value variation of noise

2.2 真实环境下的实验分析

定位实验选择在上海理工大学光电信息与计算机工程学院九楼进行。该楼层为教师集中办公区域，另外还有会议室，休息区(放置了多张沙发和长椅)等，室内环境具有一定的代表性。本文实验选择在9楼两侧走廊及中间大厅进行，定位区域大小为36 m×15 m，两侧走廊中间的装饰天花板上各放置了9个锚节点，共18个锚节点。锚节点沿东西走向每隔4.2 m依次放置，天线垂直探下，避免无线信号被天花装饰板遮挡。采集过程为正常办公时间，存在少量的一定的人员走动干扰的因素。在数据采集阶段，按照1.8 m的采样间距依次对划分的位置网格采集RSSI，完成整个9楼的位置指纹信息采集任务。由于墙壁阻挡的原因，只能采集两侧走廊和中间大厅的位置指纹信息，在采集RSSI数据过程中，会出现在某些位置点接收不到无线信号的情况，在后续匹配算法中，将接收不到无线信号的RSSI值记成-100 dBm。在采集过程中共采集了90个位置指纹，每个离线位置点连续不断采集2 min，对采集到每个锚节点的所有RSSI值做平均处理，最后构建位置指纹数据库。

图6给出了数据采集过程中，在某一离线位置接收到来自某一个锚节点的RSSI信号分布直方图，其中曲线表示RSSI信号分布的概率密度函数。由图6可知，RSSI是随着时间变化的，具有时变特性。

为进一步验证在线匹配算法的定位性能和精度，在实验环境中随机测量了21个目标点，每个目标点连续采集2 min RSSI值，对收到的每个锚节点的所有RSSI值做平均处理，高斯核函数带宽取8，正则化参数η=5.0×10-5，然后用KRR和WKNN算法对目标点进行定位。图7为KRR与WKNN在不同的K取值下的定位误差分布图，从图7中可以看出21个目标点中有15个点采用KRR算法，定位误差明显小于WKNN算法，计算不同算法下21个目标点的平均定位误差：KRR为1.58 m，K=6时，WKNN算法为2.53 m，K=7时，WKNN算法为2.37 m，K=8时，WKNN算法为2.39 m。

图6 RSSI信号分布直方图Fig.6 Histogram of RSSI signal distribution

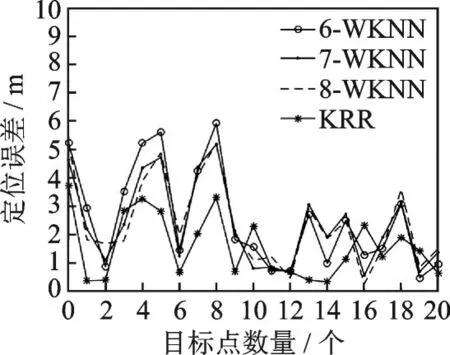
图7 定位误差分布图Fig.7 Location error distribution diagram

除此之外，还考察了锚节点与网格大小的不同分布密度对两种算法的影响，首先考虑锚节点的数量，实验中离线位置点为90个，WKNN中K取6，表1为布置6个，9个，14个，18个锚节点时两种算法的平均定位误差。从表1中可以看出，KRR算法的平均定位误差比WKNN的平均定位误差低，KRR算法的平均定位误差随着锚节点数量的增加而减小，在锚节点为18个时，平均误差为1.58 m，远远低于WKNN算法，而锚节点的数量变化对WKNN算法影响不是很大，而当锚节点为14个时，两种算法的平均定位误差都高于锚节点数量为9个时，可见锚节点的选取和当时环境的变化也会影响到定位的精度。

表2是网格大小分别为5.4 m×1.8 m，3.6 m×1.8 m，3.6 m×3.6 m，1.8 m×1.8 m时两种算法的平均定位误差。在这个实验中锚节点设置为18个，WKNN中取6。从表2中可以看出，KRR算法的平均定位误差比WKNN的平均定位误差低，KRR算法的平均定位误差随着网格密度的增加而减小，网格大小为5.4 m×1.8 m时，平均定位误差为2.24 m，网格大小为1.8 m×1.8 m时，平均定位误差为1.58 m，定位精度明显提高。

表1 锚节点数量变化的平均定位误差Table 1 Average positioning error of changes in the number of anchor nodes m

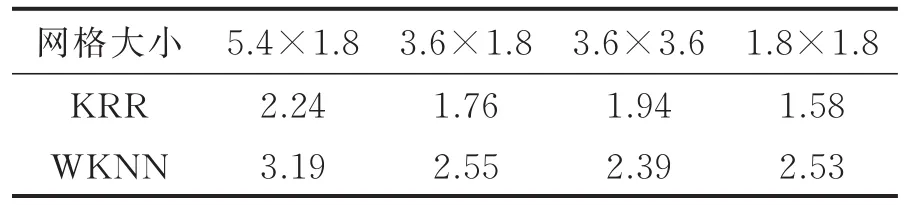
表2 网格大小变化的平均定位误差Table 2 Average positioning errors of grid size changes m

3 结束语

本文针对于WSN环境下无线传感器定位问题，提出了一种基于核岭回归的定位算法。该算法在离线阶段采用核岭回归方法训练位置指纹，得到一个输入为RSSI测量值，输出为物理位置的模型，在线定位阶段用该模型对目标进行定位。仿真和实验结果表明，该方法在精度上优于KNN、WKNN方法，可有效抑制室内环境变化引起的RSSI测量值扰动对目标定位性能的影响。虽然仿真和实验都分析了锚节点数量和网格密度大小对KRR算法的影响，但并没有考虑不同的监测区域下，锚节点数量和网格密度大小如何取值能使KRR算法在精度达到最优，而且KRR算法计算量较大，如何能使KRR算法在计算复杂度上减小有待下一步解决。