考虑温度效应的斜齿轮时变啮合刚度解析算法
2020-03-02林腾蛟赵子瑞江飞洋陈兵奎
林腾蛟,赵子瑞,江飞洋,陈兵奎
(重庆大学机械传动国家重点实验室,重庆400044)
齿轮系统作为机械装置中最为广泛的动力和运动传递形式,正朝着大功率、高转速、低噪声和轻量化方向发展.在高速重载工况下,由于啮合齿面相对滑动速度大,瞬时温升高,直接影响齿轮系统内部的温度分布,引起结构热应力及热变形,进而对齿轮啮合刚度产生较大影响,而准确高效的啮合刚度计算方法又是齿轮系统动力学分析的关键.因此,综合考虑温度影响,开展斜齿轮时变啮合刚度解析算法研究,对高速重载齿轮系统动力学设计有着重要的工程意义.
近年来,对于齿轮系统时变啮合刚度的研究非常活跃.在解析算法方面,Cui等[1]、Chaari等[2]和Liang等[3]基于材料力学理论,运用势能法计算了直齿轮的啮合刚度;在直齿轮啮合刚度算法的基础上,Wan等[4]提出了一种累积积分势能法计算斜齿轮的啮合刚度,并研究了齿轮参数与齿根裂纹对啮合刚度的影响;万志国等[5]、刘文等[6]考虑了基圆与齿根圆不重合的问题,运用势能法分别提出了求解直齿轮及斜齿轮啮合刚度的改进算法.在有限元法方面,Cooley等[7]、Liang等[8]提出了多种基于有限元法的直齿轮时变啮合刚度计算方法,并评估了各种方法的应用条件及优缺点;Fernandez等[9-10]和Ma等[11]综合考虑加工误差、齿顶修形或齿轮摩擦等非线性因素,采用有限元法与弹性接触理论相结合的方式,计算了直齿轮的时变啮合刚度.在考虑温度效应方面,苟向锋等[12]建立了由齿面接触温度变化引起直齿轮齿廓形变的数学表征,而后基于Hertz接触理论研究了接触温度对直齿轮啮合刚度的影响;罗彪等[13]基于石川模型,将轮齿齿廓简化为由梯形和矩形组成的当量齿形,综合考虑温度对直齿轮刚度的影响,引入了热刚度的概念,并提出了一种直齿轮热刚度的解析算法,计算结果与有限元法基本吻合.目前有关考虑温度效应的齿轮啮合刚度研究已取得一定的成果,但有限元法计算规模较大,解析法仅针对直齿轮开展了相关研究,关于考虑温度效应的斜齿轮时变啮合刚度解析算法鲜有报道.
在上述研究成果的基础上,本文以斜齿轮副为研究对象,提出一种考虑温度效应的斜齿轮啮合刚度解析算法.将轮齿简化为齿根圆上的变截面悬臂梁,基于切片法和积分思想,在考虑基圆与齿根圆不重合因素的同时,计入齿面接触温度变化引起的轮齿齿廓形变,以确保啮合刚度计算结果准确性;而后分析摩擦因数、输入转矩、输入转速等工况参数对斜齿轮啮合刚度的影响规律.
1 考虑热变形的斜齿轮端面齿廓方程
1.1 斜齿轮基体热变形
斜齿轮副达到热平衡状态后,本体温度场基本稳定,但各处温度非均一.对于齿轮基体,尽管本体温度场稳定,但与轮齿相固联的基体部分温度不同,因此将斜齿轮基体温度场处理为无内热源稳态非均匀温度场,其在柱面坐标系下的导热微分方程为[14]:

式中:T为斜齿轮基体内任意点的温度;r、φ、z分别为柱面坐标系中的坐标分量;λ为材料热膨胀系数.
假定斜齿轮副啮合为理想接触,沿齿面无偏载,且轮齿膨胀导致齿侧间隙减小后仍可保证最小油膜厚度.设热平衡状态下,斜齿轮基体温度仅随径向坐标r变化,即一维稳态温度场,则导热微分方程(1)可简化为:

其积分解为:

式中:C1、C2均为积分常量.满足热力学第一类边界条件,即r=Ri时,T=T(Ri);r=R0时,T=T(R0),将其代入微分方程通解(3)中解得斜齿轮基体温度为:
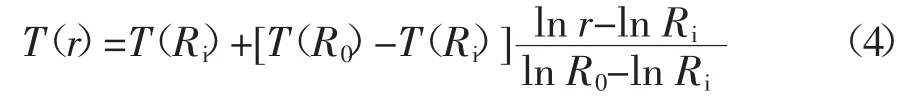
式中:Ri为斜齿轮的轴孔半径;T(Ri)为热平衡时斜齿轮的轴孔温度;R0=max(Rb,Rf),Rb为基圆半径,Rf为齿根圆半径;T(R0)为热平衡时基体相应柱面的温度.
当不考虑外力、表面残余应力等因素的作用,即认为柱体的应力仅由温度改变而引起的,按位移法求解基体的热变形,得到基体径向位移函数为:

式中:u为基体内任一点的径向位移;υ为泊松比.
当Rb>Rf时,有R0=Rb,令r=Rb,将式(4)代入式(5)可得热平衡时斜齿轮基圆的热变形量:

同理,令r=Rf,可得热平衡时齿根圆的热变形量:

当Rf>Rb时,则有R0=Rf,令r=Rb,将式(4)代入式(5)可得热平衡时斜齿轮基圆的热变形量:

同理,令r=Rf,可得热平衡时齿根圆的热变形量:
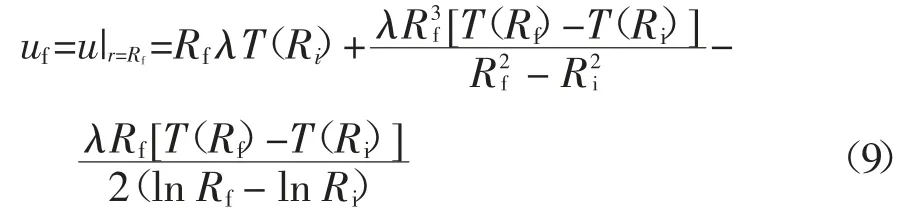
1.2 热平衡时斜齿轮的端面齿廓方程
当斜齿轮受热变形时,基圆半径增加,齿轮实际齿廓在齿厚和齿高方向都将发生热膨胀,其中端面齿廓如图1所示.仅考虑齿面接触温度对齿廓曲线的影响,则实际端面齿廓上任一点的半径为:
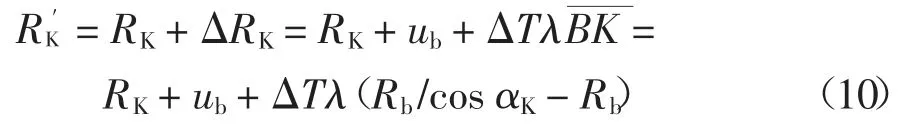
根据几何关系,展角改变量为:

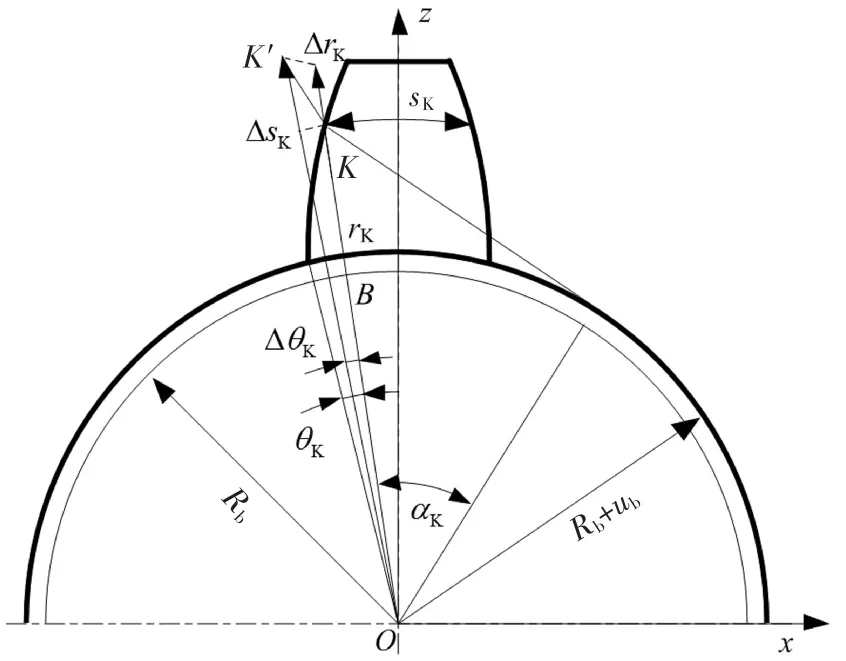
图1 斜齿轮端面齿廓热膨胀示意图Fig.1 Sketch map of thermal expansion of gear transverse profile
斜齿轮热变形后端面齿廓极坐标参数方程为:
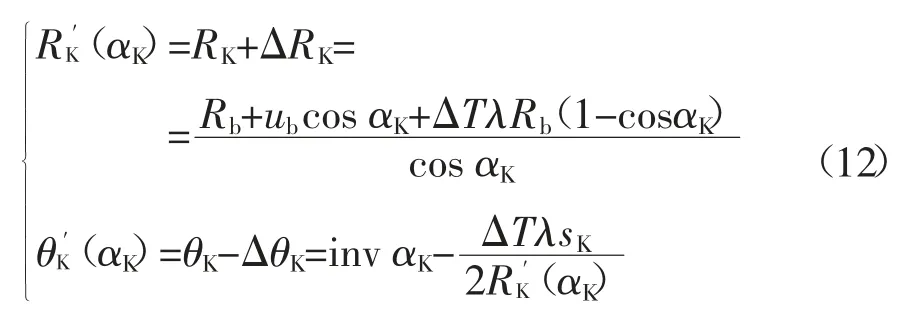
式中:αK、RK分别为不计热变形时端面齿廓上任一点K的压力角和半径;sK为不计热变形时端面齿廓上任意圆的齿厚;ΔT为啮合齿面瞬时闪温,其表达式为[12]:

式中:ψT为斜齿轮温升系数;fm为平均摩擦因数;fe为单位齿宽上的齿面法向载荷;vi、gi、ρi、ci(i=1,2)分别为主、从动轮的齿面切向速度、热传导系数、材料密度以及比热容;Bc为接触带半宽.
2 考虑温度效应的时变啮合刚度算法
啮合刚度是随啮合齿数和轮齿接触位置周期变化的时变函数,由于斜齿轮存在螺旋角,啮合过程由轮齿一端面进入啮合到另一端面退出啮合,接触线长度具有时变性,其啮合刚度算法与直齿轮不同.基于积分方法,将其轮齿沿齿宽方向切分成若干薄片,每一薄片可近似视为直齿轮,通过计算各薄片的啮合刚度并积分,即可得到斜齿轮啮合刚度.
综合考虑轮齿接触、弯曲、剪切、轴向压缩及基体弹性刚度,采用能量法计算斜齿轮副啮合刚度,其综合啮合刚度可表示为:
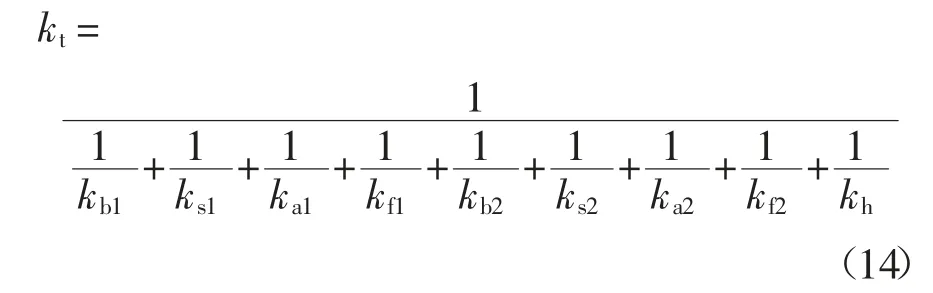
式中:kb为弯曲刚度;ks为剪切刚度;ka为轴向压缩刚度;kf为基体弹性刚度;kh为接触刚度.
2.1 弯曲、剪切及轴向压缩刚度
对于高速重载齿轮传动,由于啮合齿面瞬时温升较高,斜齿轮实际截面齿廓已不再满足理论渐开线方程,存在较大的非渐开线误差.由于未考虑温度效应的斜齿轮啮合刚度算法是基于渐开线基本性质推导的,对于计及热变形的啮合刚度计算不再适用,为此需重新推导考虑温度效应的斜齿轮啮合刚度.
将轮齿假设为齿根圆上的悬臂梁,如图2所示,采用直线CC1和DD1简化表示齿根处齿廓.
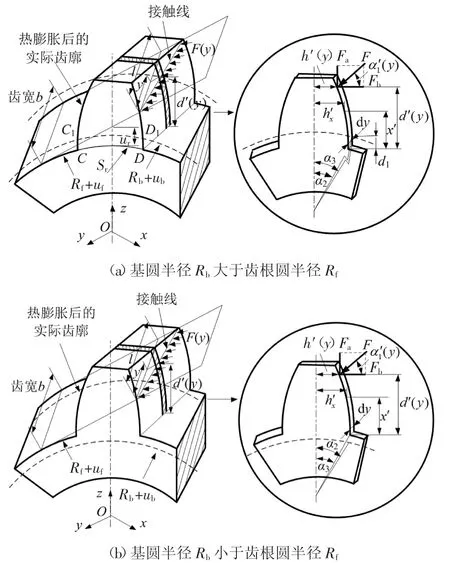
图2 考虑温度效应的斜齿轮轮齿悬臂梁模型Fig.2 Cantilever beam model of helical gear tooth considering temperature effect
将端面齿廓的极坐标参数方程转换至随动笛卡尔坐标系S(x,y,z)下.利用坐标变换,可得如下转换关系:
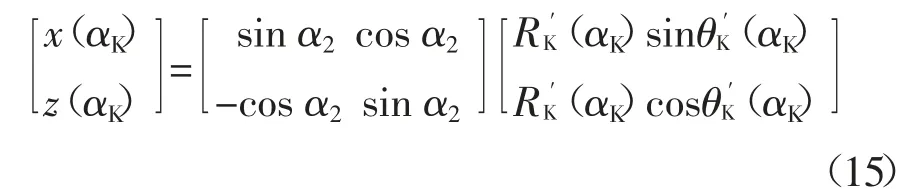
采用切片方法,厚度为dy的每一薄片轮齿的弯曲刚度可表示为:
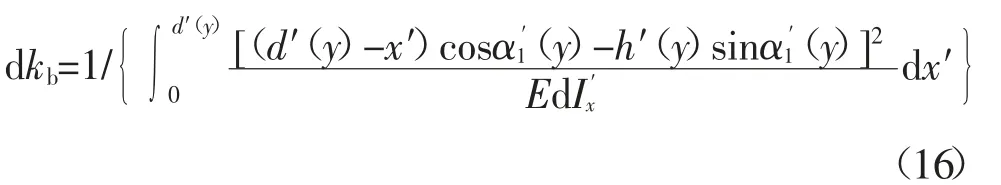
当Rb>Rf时,相关表达式为:
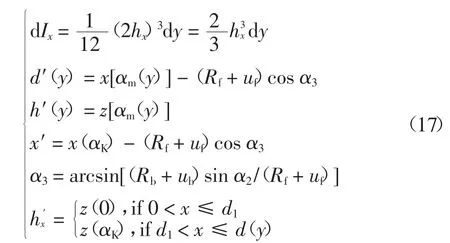
式中:αm(y)表示不计热变形时斜齿轮端面齿廓矢径在z轴的投影为h(y)时对应的压力角,其中h(y)为啮合点和齿轮中心线的距离,是轴向坐标y的函数.
将以上变量代入式(16)得到每一薄片轮齿的弯曲刚度dkb,而后对其积分即可得到考虑温度效应的斜齿轮弯曲刚度kb:

式(18)不可积分,因此采用求和方法替代积分方法求解斜齿轮的啮合刚度,于是斜齿轮弯曲刚度kb可重新表示为:

式中:Δy=l/N;l为时变接触线长度L在齿宽方向上的投影,l=Lcosβb;N为斜齿轮沿齿宽方向切分的切片份数.根据单齿接触线长度表达形式[6],(y)的求解方法如下.
当端向重合度大于轴向重合度(εα>εβ)时,啮合力F与主动轮轮齿中心线垂直方向的夹角为:
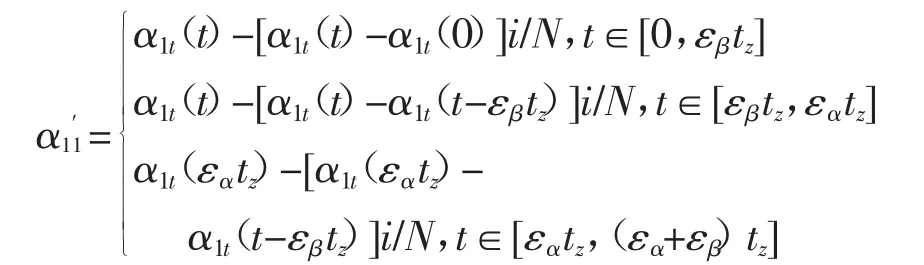
其中,α1t(t)为在主动轮端面齿廓上对应的角度,其表达式为:
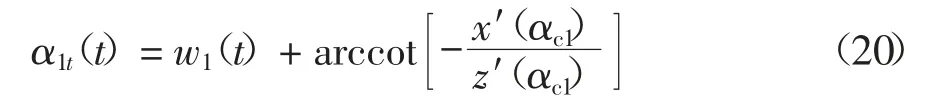
式中:αc1为主动轮进入啮合时端面齿廓处的压力角.可由下式计算得到:
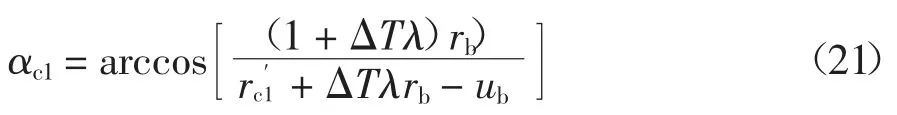
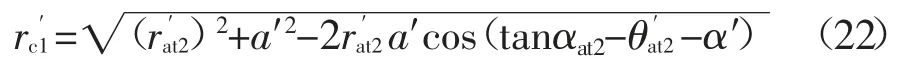
式中:a′代表实际中心距;α′表示啮合角;αat2为从动轮端面齿顶圆压力角.

其中,α2t(t)为在从动轮端面齿廓上对应的角度,其表达式为:
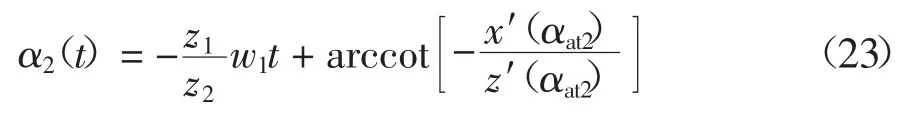
同理,当端向重合度小于轴向重合度(εα<εβ)时,啮合力F与主动轮轮齿中心线垂直方向的夹角为:
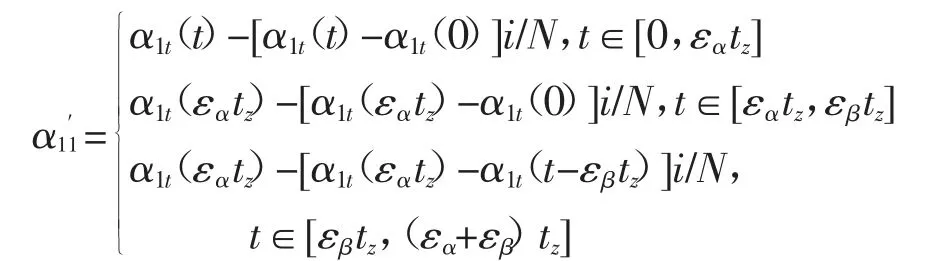

同求解弯曲刚度kb的过程类似,考虑温度效应的斜齿轮剪切刚度ks和轴向压缩刚度ka分别为:
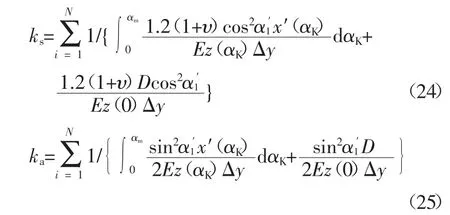
式中:D=(Rb+ub)cosα2-(Rf+uf)cosα3.
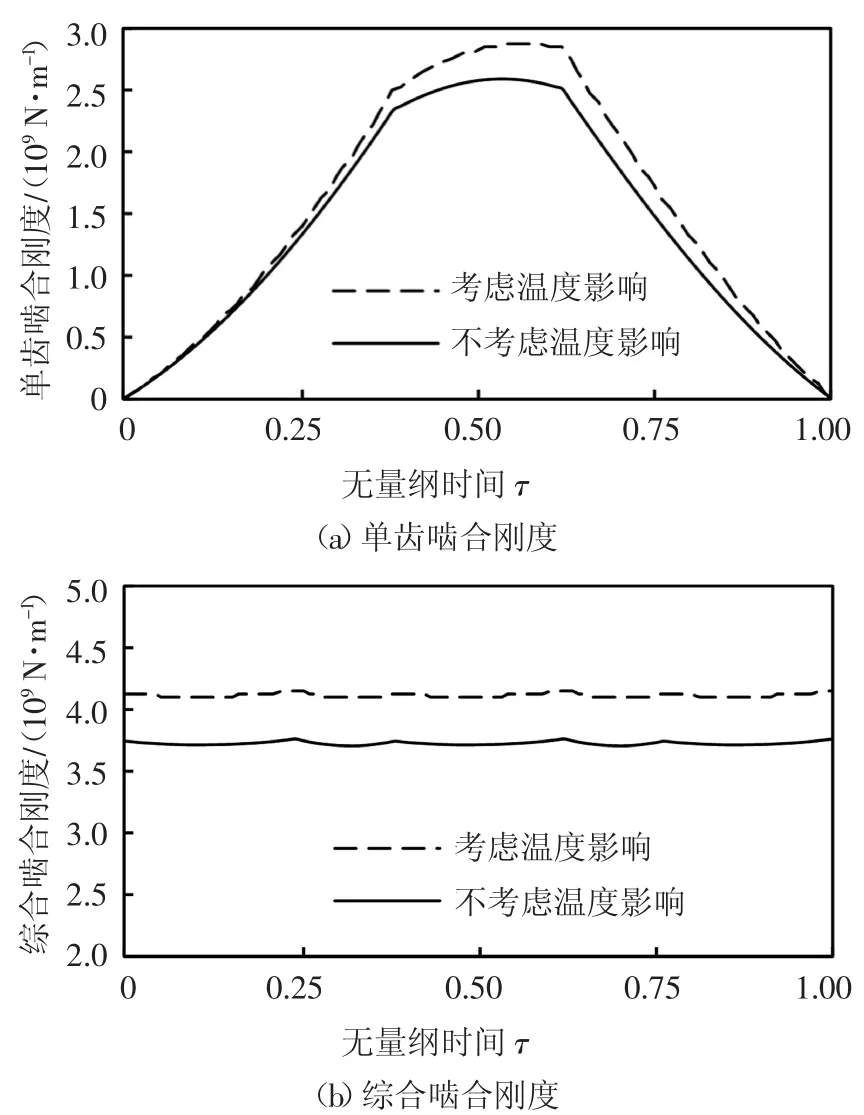
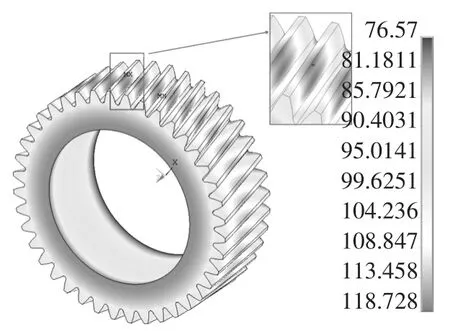
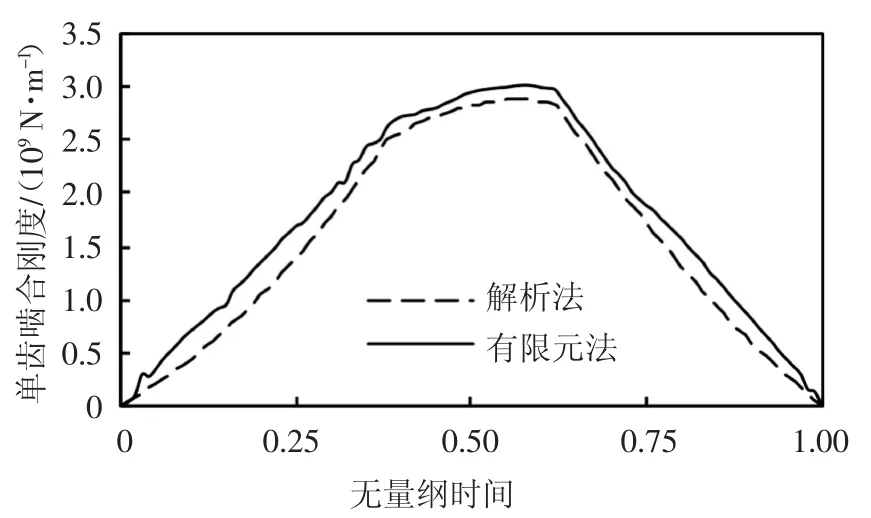
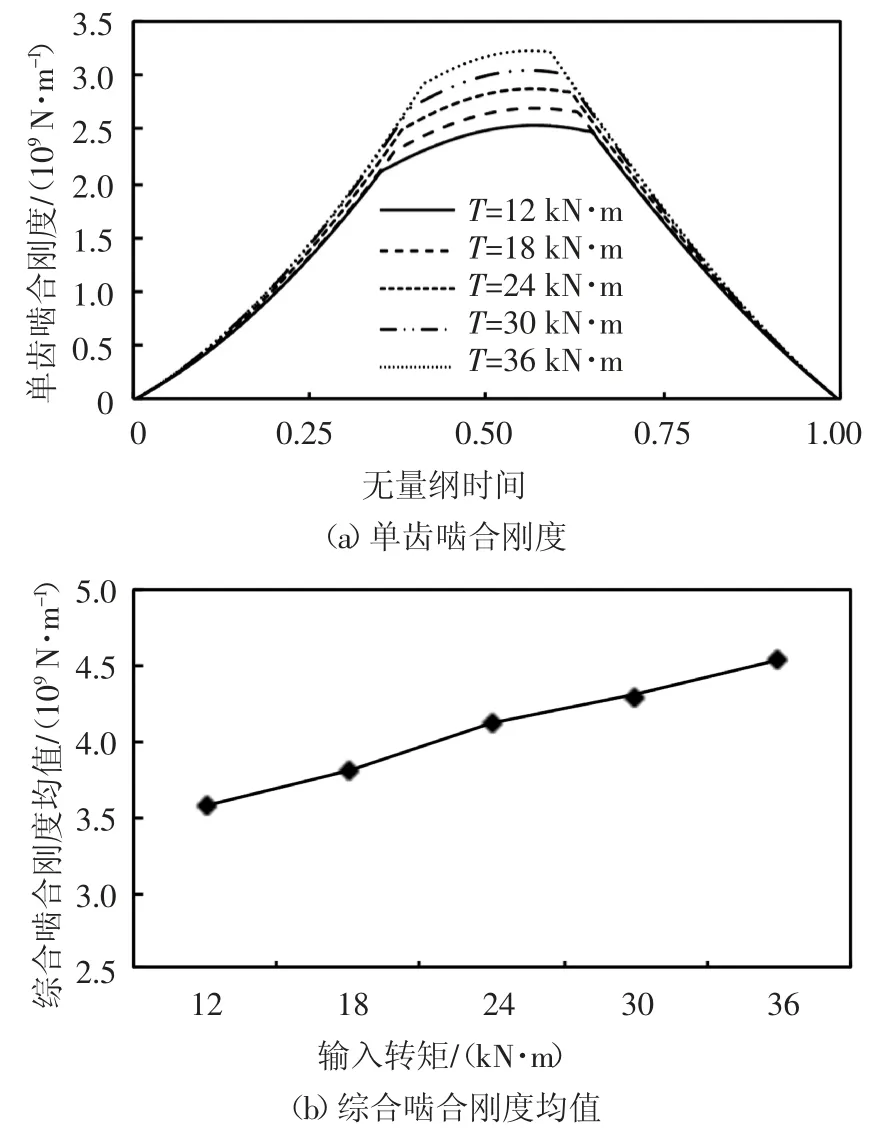
当Rb 式中:αf为齿根圆压力角. 将每一片轮齿薄片的基体刚度对y进行积分,即可得到轮齿基体刚度[2],其表达式为: 式中:L*、M*、P*、Q*均为尺寸系数,其计算式参见文献[2].ur和Sr如图2(a)所示,其表达式为: ur=x[αm(y)]-(Rf+uf) Sr=2(Rf+uf)α3 根据赫兹接触理论,啮合斜齿轮副的赫兹接触刚度kh可表示为: 式中:E为弹性模量;L为时变接触线长度. 表1给出了一对斜齿轮副的基本参数,综合考虑温度对啮合刚度的影响,分别采用本文中的解析算法和有限元法计算斜齿轮的时变啮合刚度,以验证解析算法的准确性. 表1 斜齿轮副基本参数Tab.1 Basic parameter of helical gear pair 采用本文给出的解析算法,计算考虑温度影响前后斜齿轮的时变啮合刚度,得到如图3所示的单齿啮合刚度和综合啮合刚度曲线,图中横坐标τ为无量纲时间,表示轮齿从啮入到啮出的整个过程,τ=t/tε,其中t为时间变量,tε为单齿啮合时间. 图3 考虑温度影响前后啮合刚度对比曲线Fig.3 Comparison curve of mesh stiffness with and without temperature effect 由图3可知,考虑温升影响后,由于齿廓热膨胀导致齿侧间隙减小,轮齿接触区域变大,接触区域平均变形量减小,故斜齿轮副从啮入到啮出整个过程的啮合刚度均有所增大.其中,单齿啮合刚度在啮入和啮出端的增大量较小,在节点附近的增大量较大,最大值由2.592×109N/m增至2.878×109N/m;综合啮合刚度均值由3.726×109N/m增至4.117×109N/m. 主、从动轮齿面摩擦热流密度由齿面摩擦因数、相对速度和齿面接触压力确定,其计算式分别为: 式中:pNc为啮合齿面的接触压力;β为主、从动轮热流密度的分配因子,其计算式参见文献[15]. 齿轮对流换热系数可分为齿轮端面对流换热系数ht及齿面对流换热系数hs两类.将端面对流换热简化为旋转圆盘的对流换热求解,其计算式为[15]: 式中:Nur为Nusslet系数;ζ为指数常数;Re为雷诺数;υ0为润滑油的运动黏度. 由间歇冷却理论可得齿面对流换热计算式为[15]: 式中:qtot为标准化总冷却量的渐近水平;η0=g0/ρ0c0为热扩散系数;g0、ρ0、c0分别为润滑油的热传导系数、密度和比热容;A为齿面表面积. 利用APDL参数化语言建立啮合斜齿轮副三维实体模型,采用SOLID70单元以及SURF152单元进行有限元网格划分,施加啮合齿面摩擦热流密度以及齿轮端面和齿面对流换热系数,求解斜齿轮副的本体温度场,计算结果如图4所示;而后采用静态接触分析方法,对主动轮内圈节点施加转矩,并约束其轴向和径向位移;对从动轮内圈节点施加全约束;同时将温度场结果以载荷形式施加至有限元模型,通过提取齿轮副在啮合周期内的法向载荷以及综合变形,如图5所示,计算斜齿轮副的时变啮合刚度,其计算式为: 式中:Fn为啮合齿面的法向载荷;δn为计及温度影响后主从动齿轮在啮合区域的综合变形. 图4 主动轮本体温度分布Fig.4 Bulk temperature distribution of driving gears 图5 主动轮综合变形云图Fig.5 Integrated deformation nephogram of driving gears 对比本文所提解析算法和有限元法的计算结果,得到如图6所示考虑温度效应的斜齿轮单齿啮合刚度曲线.由图6可知,解析算法与有限元法计算结果在节点附件最为接近,在啮入和啮出端误差相对较大,二者的变化趋势完全一致,单齿啮合刚度最大值分别为2.878×109N/m和3.020×109N/m,单齿啮合刚度平均值误差为11.59%,误差在可接受范围内. 图6 单齿啮合刚度对比曲线Fig.6 Comparison curve of single mesh stiffness 工况参数将影响齿轮的本体温度场,进而引起轮齿时变啮合刚度的变化.本节针对表1所示的斜齿轮副,通过改变摩擦因数、输入转矩和输入转速,开展考虑温度效应的时变啮合刚度影响规律研究. 摩擦因数增大将引起齿面摩擦热流量增加,进而使齿轮本体温度及啮合齿面瞬时闪温升高.选取摩擦因数f的变化范围为0.03~0.07,不同摩擦因数下的单齿啮合刚度和综合啮合刚度均值分别如图7所示.由图7可知,考虑温度影响后,随着摩擦因数的增大,单齿啮合刚度整体上呈增大趋势;由于摩擦因数增大不影响齿轮副的重合度,因此综合啮合刚度均值也随单齿啮合刚度的增大而增大.当摩擦因数f由0.03增至0.07时,啮合刚度均值由3.858×109N/m增至4.311×109N/m,提高了11.74%. 图7 不同摩擦因数下的斜齿轮啮合刚度Fig.7 Mesh stiffness of helical gears with different friction coefficients 输入转矩增大使齿面接触压力增大,进而使齿面摩擦热流量增加,齿轮本体温度及啮合齿面瞬时闪温随之升高.保持输入转速1 200 r/min不变,输入转矩T变化范围为12~36 kN·m,不同转矩下的单齿啮合刚度和综合啮合刚度均值分别如图8所示.由图8可知,考虑温度影响后,随着载荷的增大,轮齿接触迹线增长,单位线载荷减小,单齿啮合刚度随之增大;由于接触迹线增长一定程度上使齿轮副的重合度增加,因此综合啮合刚度均值接近线性规律增大.当输入转矩T由12 kN·m增至36 kN·m时,啮合刚度均值由3.586×109N/m增至4.454×109N/m,提高了24.21%. 图8 不同输入转矩下的斜齿轮啮合刚度Fig.8 Mesh stiffness of helical gears with different input torques 输入转速增大使齿面切向速度增大,从而使齿轮本体温度及啮合齿面瞬时闪温也相应升高.保持输入转矩24 kN·m不变,输入转速n的变化范围为1 200~6 000 r/min,不同输入转速下的单齿啮合刚度和综合啮合刚度均值分别如图9所示.可以看出,考虑温度影响后,随着输入转速的增大,单齿啮合刚度及综合啮合刚度均值随之增大,且增大幅度有所减小.当输入转速n由1 200 r/min增至6 000 r/min时,啮合刚度均值由4.118×109N/m增至4.554×109N/m,提高了10.59%. 图9 不同输入转速下的斜齿轮啮合刚度Fig.9 Mesh stiffness of helical gears with different input speeds 1)将轮齿简化为齿根圆上的变截面悬臂梁,计入齿面接触温度变化引起的轮齿齿廓形变,基于势能法提出了一种考虑温度效应的斜齿轮啮合刚度解析算法,通过与有限元法计算结果对比分析,验证了解析算法的准确性,提升了斜齿轮啮合刚度的计算效率. 2)考虑斜齿轮温升影响后,轮齿从啮入到啮出整个过程的啮合刚度均有所增大.对于单齿啮合刚度,在啮入和啮出端增大量较小,在节点附近增大量较大. 3)通过不同摩擦因数、输入转矩、输入转速等工况参数对斜齿轮啮合刚度的影响分析,得出考虑温度效应后单齿啮合刚度及综合啮合刚度均值均随上述工况参数的增大而增大,其中输入转矩对啮合刚度的影响最大.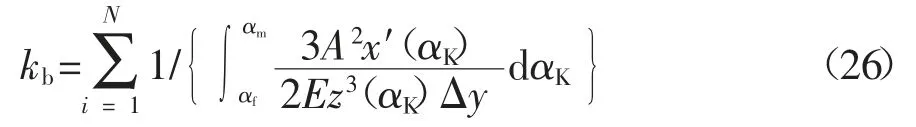
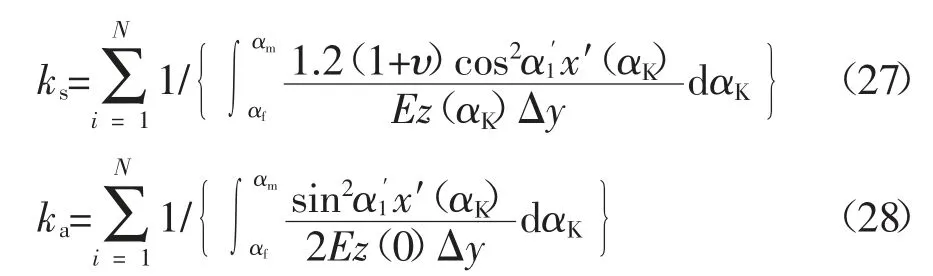
2.2 基体弹性刚度
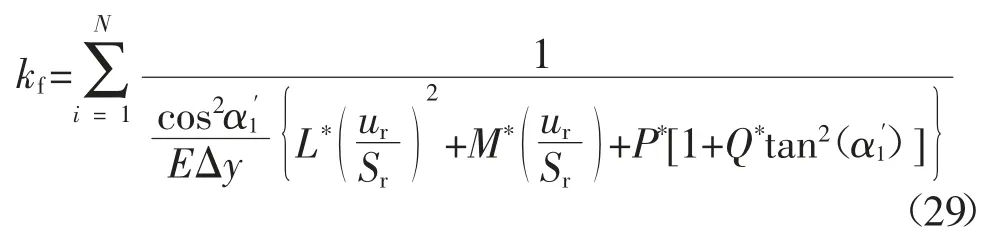
2.3 赫兹接触刚度

3 计及温度影响的时变啮合刚度计算

3.1 考虑温度效应的斜齿轮啮合刚度计算结果
3.2 斜齿轮副啮合刚度有限元模型

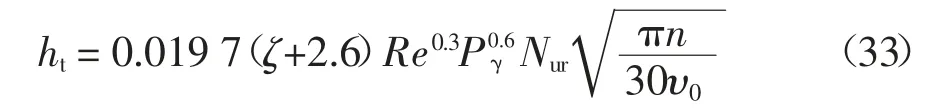
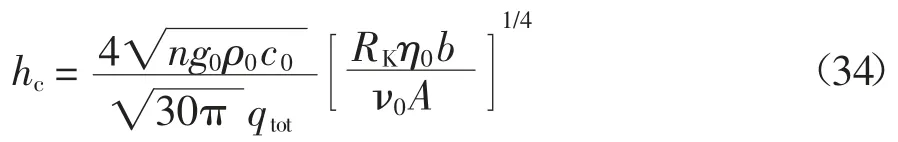


3.3 啮合刚度算法对比验证
4 工况参数对斜齿轮啮合刚度影响分析
4.1 摩擦因数

4.2 输入转矩
4.3 输入转速

5 结论
