数控凸轮轴磨床颤振稳定性研究

张氢，陈文韬，陈淼，王玉琢，郑大腾

（1.同济大学 机械与能源工程学院，上海201804；2.江西杰克机床有限公司，江西 吉安343008；3.井冈山大学 机电工程学院，江西 吉安343009）

凸轮轴是内燃发动机的关键零件之一，它的加工精度和质量直接影响发动机的使用寿命、节能和效率.汽车、飞机行业对发动机性能需求的不断提升，对凸轮轴的高精度磨削提出了更高的要求[1].在磨削加工过程中，颤振现象导致的不稳定磨削将影响工件表面质量，特别是磨削波纹表面而引起的再生型颤振是产生颤振的主要原因[2].相对车削和铣削等单主轴运动加工方式，磨削加工中包含了工件和砂轮绕各自主轴的旋转，运动方式更加复杂.

目前，国内外学者已经对磨床的再生颤振进行了大量的研究.Li等[3]通过特定工艺条件的改变，确定了外圆磨削系统的颤振边界条件.钟建琳等[4]通过模态测试实验获得外圆磨削的动力学参数并以此绘制了磨削的稳定性极限图.Chi等[5]针对外圆切入磨建立了基于接触刚度与系统固有频率关系的动力学模型.Leonesio等[6]提出了一种通过冲击实验测量系统响应获得磨削过程的等效刚度和阻尼的频域识别方法.Weck等[7]建立了外圆磨削再生颤振模型，并对磨削稳定性机理进行了研究.Paris等[8]考虑系统刚度与阻尼对稳定性的影响，建立了高速铣床的稳定性动力学模型.蒋永翔等[9-10]同时考虑工件和砂轮的再生效应，建立外圆纵磨以及外圆切入磨的工件、砂轮再生颤振动力学模型.Jiang等[11]利用稳定性叶瓣图法进行了稳定性预测研究.Yan等[12]提出了一个同时考虑工件横向运动和扭转运动的外圆切入磨动力学模型，并利用该模型绘制稳定性图.任成高等[13]通过变速磨削颤振实验，证明变速磨削能在一定程度上抑制高速磨削颤振.Barrenetxea等[14]、Ahrens等[15]通过理论稳定图和实验结果相结合，验证了新型无心磨削和切入磨颤振抑制技术的有效性.

上述研究主要是针对外圆磨削，对以凸轮轴磨床为代表的非圆磨削的颤振研究相对较少.本文以某型高精度随动数控凸轮轴磨床为研究对象，同时考虑工件和砂轮的再生效应建立动力学模型并绘制磨削稳定性极限图；在颤振实验的基础上利用频域和时频域方法分析磨床的振动特性，并验证动力学模型的正确性.

1 凸轮轴磨床再生型颤振动力学建模

本文研究的是某公司自主研发的高精度随动数控凸轮轴磨床，是一种切入磨磨床，通过数控系统的控制，使磨床砂轮架进给运动与头架主轴旋转运动实现跟随联动.在实际加工过程中，磨床系统往往会受到大量来自外界的干扰，这些外界激励将引起砂轮和凸轮轴在砂轮进给方向上的相对振动，并留下振纹.由于振纹的存在，在凸轮轴高速磨削的过程中磨削深度和磨削力呈周期性变化，产生的新振源会引起磨床系统振动，即再生效应，由此引发工件与刀具之间强烈的再生型自激颤振.

随动数控凸轮轴磨床类似于外圆切入磨磨床，在其磨削加工过程中凸轮轴与砂轮将分别绕各自主轴旋转，同时砂轮架以一定线速度做切向进给运动.与外圆磨床不同的是，砂轮架除了磨削进给外，根据凸轮轴转速和凸轮轴外形作周期性随动运动.该运动一方面成为磨床的内部振源影响磨床的加工性能，另一方面在磨削过程中和凸轮轴主轴转动耦合，对凸轮轴轮廓精度及恒线速度磨削提出了更高的要求.为了减小随动运动对磨削的影响，凸轮轴磨床的工件转速通常较小，远小于外圆磨床的工件转速.本文研究的数控凸轮轴磨床振动系统可分解为砂轮和凸轮轴两个系统.首先研究砂轮系统，在磨削深度方向上可将砂轮视为一个单自由度系统，如图1所示.

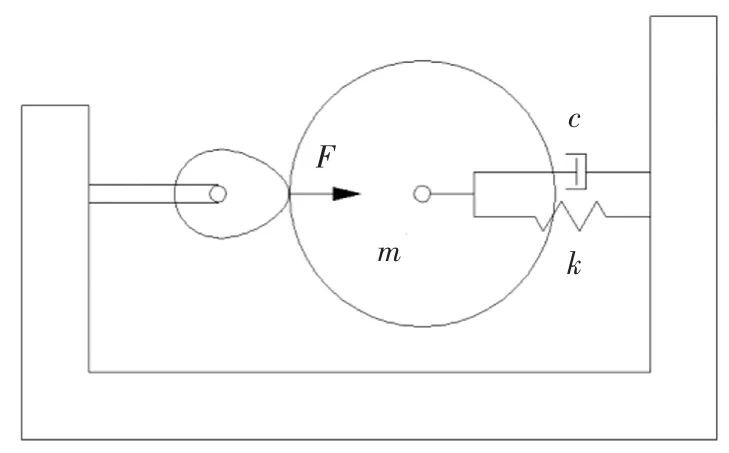
图1 砂轮系统的动力学系统模型Fig.1 Dynamic model of grinding wheel system

图1所示系统的运动微分方程为：

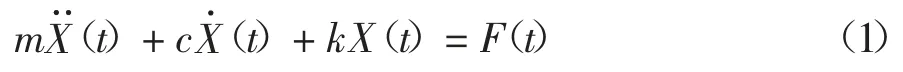
式中：m为砂轮的等效质量；c为砂轮的等效阻尼；k为砂轮的等效刚度；X（t）为t时刻砂轮的振幅；F（t）为t时刻的动态磨削力.

在t-T时刻，砂轮振幅为X（t-T）并在凸轮轴表面产生振纹，砂轮旋转一周后砂轮在凸轮轴表面振纹的干扰下振动，振幅为X（t），同时在凸轮轴上产生新的振纹，则t时刻凸轮轴表面的动态振纹为：

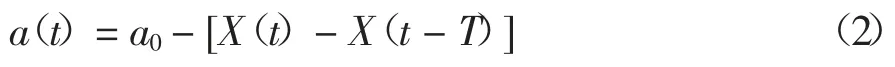
式中：a0为凸轮轴表面初始振纹；T为砂轮旋转周期.

动态磨削力可以用材料去除率表示为：

式中：ks为砂轮磨削力系数；h为砂轮磨削深度；b为磨削接触宽度.对式（2）和式（3）进行拉氏变换，可得

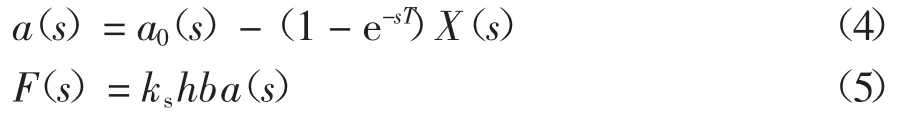
对式（1）进行拉氏变换并代入式（4）和式（5）可得：

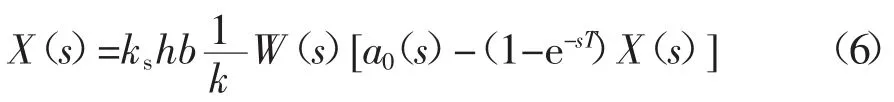
式中：W（s）为砂轮系统传递函数.可表示为：

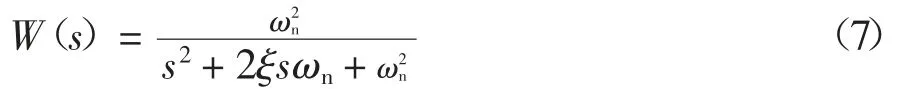
式中：ωn为砂轮固有角频率；ξ为砂轮阻尼比；s为拉氏算子；W（s）为砂轮传递函数.

对式（6）进行变换，以初始振纹a0（s）作为系统输入，以砂轮振幅X（s）作为系统输出，则砂轮系统的传递函数为：

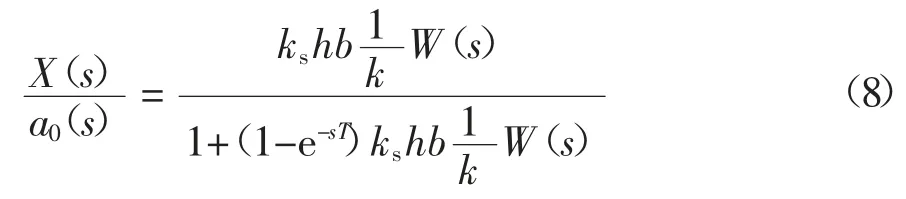
2 稳定极限条件分析

对于式（8）所表征的闭环系统，特征方程为：

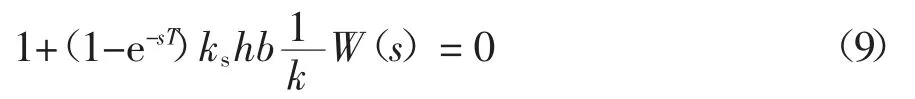
将特征根s表示为s=σ+jω的形式，并且由控制原理可知，当σ＞0时系统处于不稳定状态，磨削颤振将不断增强；当σ=0时系统处于临界稳定状态；当σ＜0时系统处于稳定状态，无磨削颤振产生.

当系统处于临界稳定状态时，s=jω，式（9）变形为：

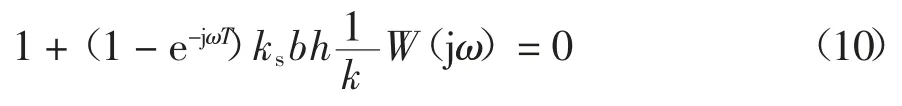
此时式中h为稳定磨削时的临界磨削深度.

将s=jω和λ=ω/ωn代入式（7）并将结果分解为实部和虚部的形式：

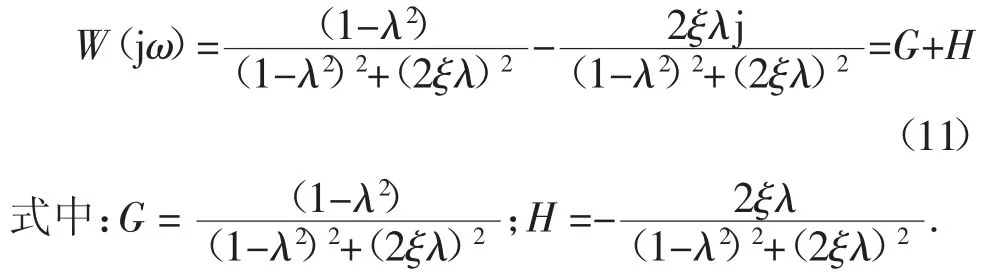
将式（11）和欧拉公式e-jωT=cosωT-jsinωT代入式（10）可得：

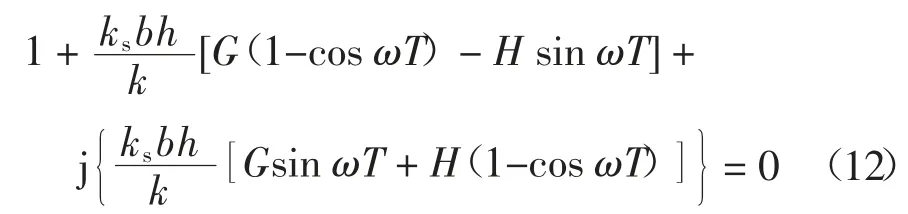
式（12）实部和虚部都为零，因此

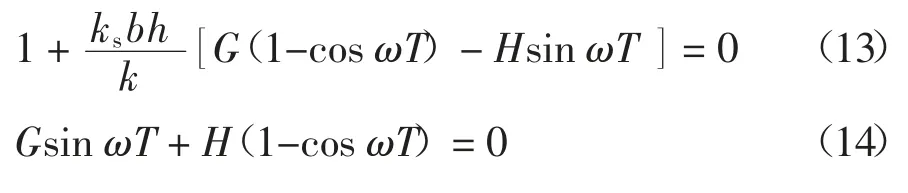
由式（13）和式（14）可得：

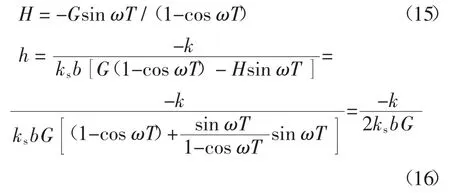
由式（14）可得传递函数的相位角φ，并由三角恒等变换可得：

由式（16）和式（18）可以得到稳定磨削时砂轮的临界磨削深度和转速，同理通过分析凸轮轴系统可得到稳定磨削时凸轮轴的临界磨削深度和转速：

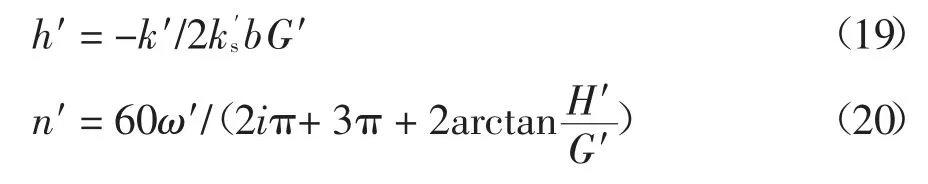
式中参数与计算砂轮体系中的相应符号的含义类似.

磨削过程中虽然磨削深度一直在动态变化，但从整个磨削过程考虑，由式（3）可知，砂轮磨削深度和凸轮轴磨削深度之比应等于凸轮轴磨削力系数与砂轮磨削力系数之比.且凸轮轴体系和砂轮体系中将有一个系统先达到不稳定状态，因此临界磨削深度为：

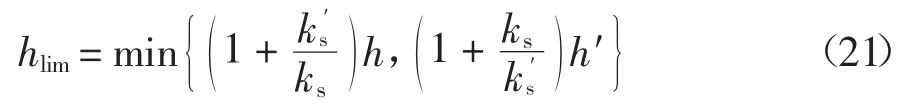
3 绘制稳定性极限图

通过求解特定加工参数下的临界磨削深度可以对磨削过程的稳定性进行预测，求解过程中所需要的动力学参数可通过对磨床进行模态实验和磨削力测试实验获得，如表1所示.

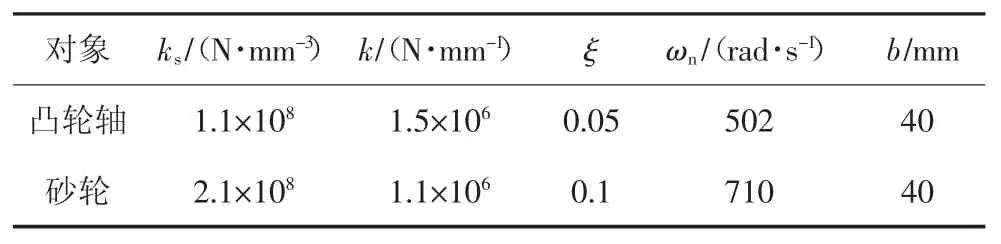
表1 求解磨削稳定极限所需参数Tab.1 Parameters needed to solve grinding stability limit

根据表1中的动力学参数绘制该磨削系统的稳定性极限图，如图2所示.曲面下方为稳定性区域，曲面上方为不稳定性区域，利用此稳定性极限图可预测磨床是否发生颤振.

图2 磨床稳定性极限图Fig.2 Stability limit diagram of grinding machine

与外圆磨床不同，凸轮轴磨床的工件转速相对较小，由图2可知，在凸轮轴磨床的工件转速范围内，改变工件转速不影响磨床的再生颤振.

4 颤振实验

本文对某新型高精度随动数控凸轮轴磨床进行颤振实验以验证所建立的磨削动力学模型.

4.1 测点布置

根据高精度随动数控凸轮轴磨床整机结构、运动关系以及模态预测试中确认的产生较大振动的部件和振动方向，在磨床响应部位上共布置12个测点，测点布置如图3所示.在每个测点上安装一个DH131E加速度传感器，用此传感器测量测点所处平面法线方向上的振动加速度.

4.2 实验方案

磨削加工中有3个重要加工参数：砂轮转速、工件转速和磨削深度.其中磨削深度越大，磨床的振动越大，为观察到明显的振动现象，取磨削深度为0.05 mm.根据实际加工过程中典型的转速组合和磨床的推荐转速范围对砂轮转速和工件转速两个因素均匀选取4个水平，实验中将各因素全部水平互相组合.实验方案如表2所示.

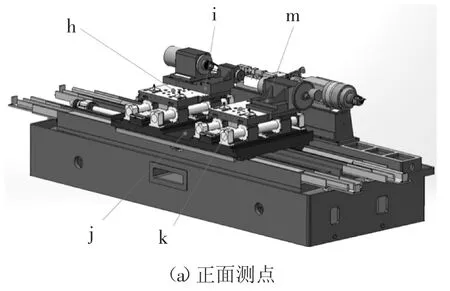
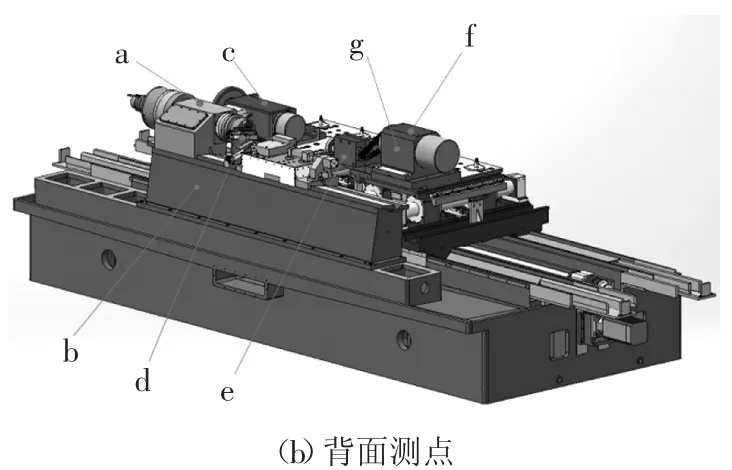
图3 测点布置Fig.3 Layout of sensors

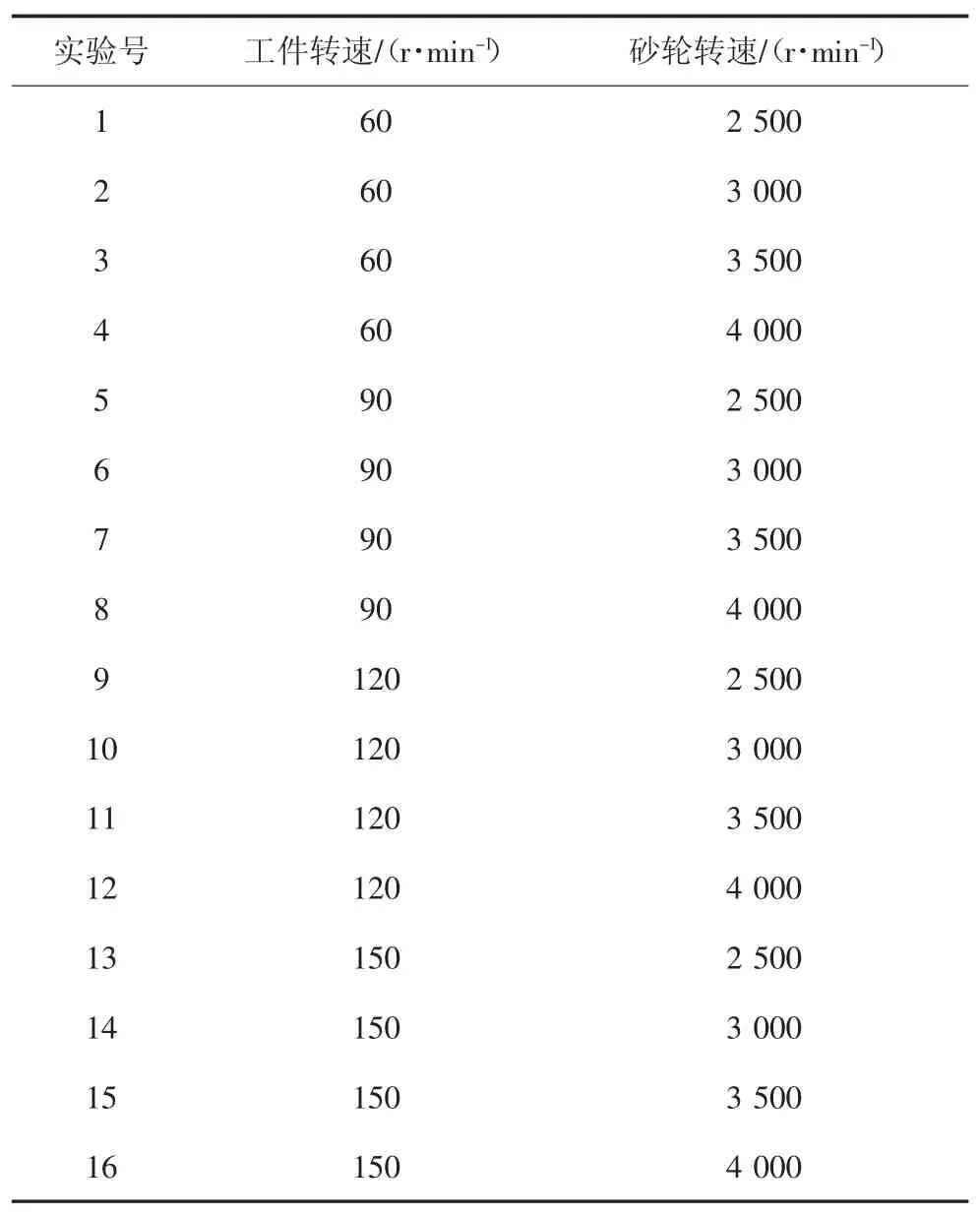
表2 实验方案Tab.2 Experimental scheme

4.3 频域与时频域分析

对磨削加工区域中的测试数据进行快速傅里叶变换可获得整个磨削过程中出现的频率成分，对测试信号进行小波变换可获得小波时频图，可与频谱图相互验证并观察各频率在时间轴上的分布情况.

根据测点与砂轮的相对位置将所有测点分为近、中、远3类，首先取最靠近砂轮的a～d号测点作为研究对象进行分析.当磨削深度为0.05 mm时，分别采用1号和4号实验，测得a号测点的数据进行频域与时频域分析.结果分别如图4和图5所示.

图4 采用1号实验时a号测点的时程图、频谱图和时频图Fig.4 Time history，frequency and time-frequency responses of point a in testing 1

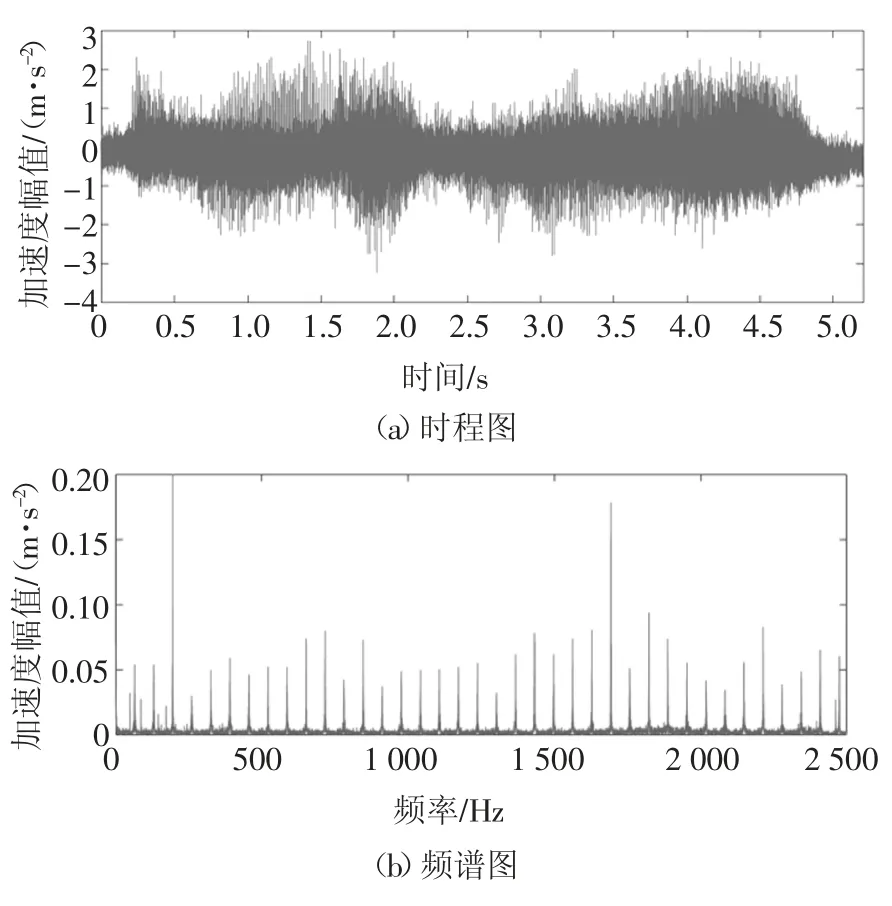
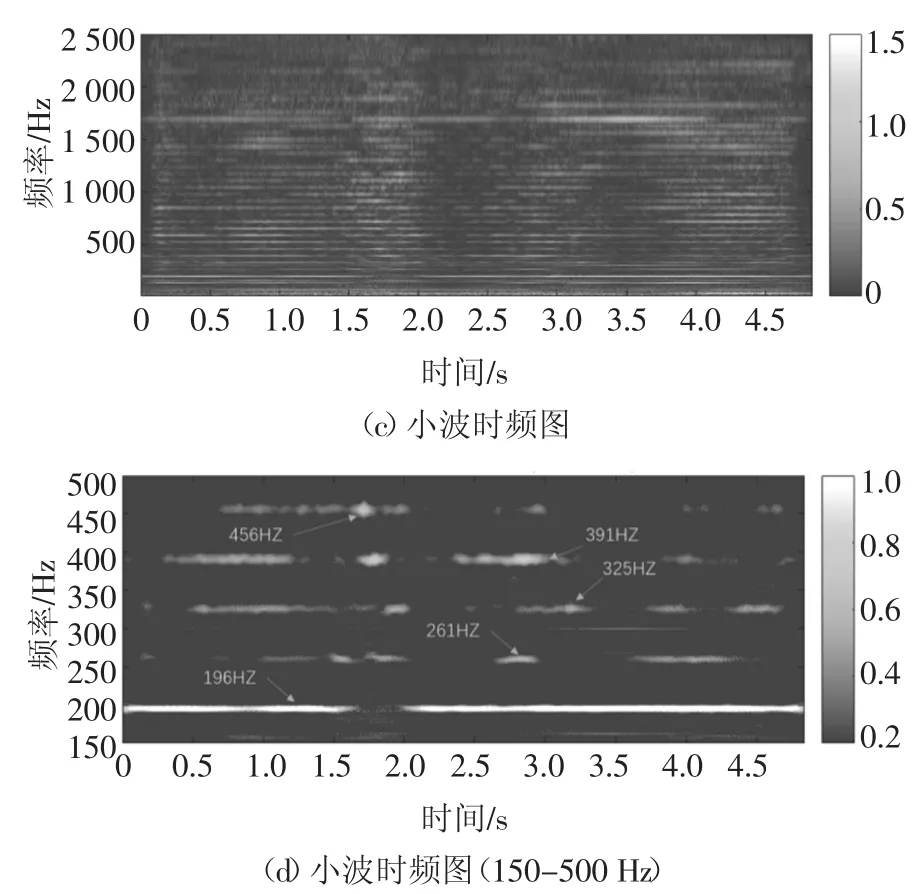
图5 采用4号实验时a号测点的时程图、频谱图和时频图Fig.5 Time history，frequency and time-frequency responses of point a in testing 4

由于时频图的频率成分比较多，选取图中振幅较大的150～500 Hz频率区间研究其时频域特点，分别如图4（d）和图5（d）所示.图4中的频率组成主要是砂轮旋转频率（42 Hz）的倍频，图5中的频率组成主要是砂轮旋转频率（66 Hz）的倍频.用同样的方法分析a～d号测点的其他数据也可以观察到类似的现象：频谱图中主要的频率组成是砂轮的旋转频率的倍频，这一现象表明在磨削过程中，砂轮的旋转成为磨床系统的内振源引起整机受迫振动.由于a～d号测点离砂轮较近，其受迫振动较为剧烈，掩盖了其他频率.观察时频图可以发现，在磨削过程初期，出现较多砂轮旋转频率倍频的振动，由此推测砂轮与凸轮轴刚接触时两者的相互作用加剧了砂轮振动，使得砂轮产生的受迫振动更加剧烈；在磨削过程中期和后期，部分频率的振幅明显减小，表明随着磨削过程的进行，磨削量减小，这种相互作用也减小，砂轮振动相对平稳.

然后取距离砂轮位置适中的e～i号测点作为研究对象进行分析，当磨削深度为0.05 mm时，分别采用1号和4号实验，测得e号测点的数据进行频域与时频域分析.结果分别如图6和图7所示.

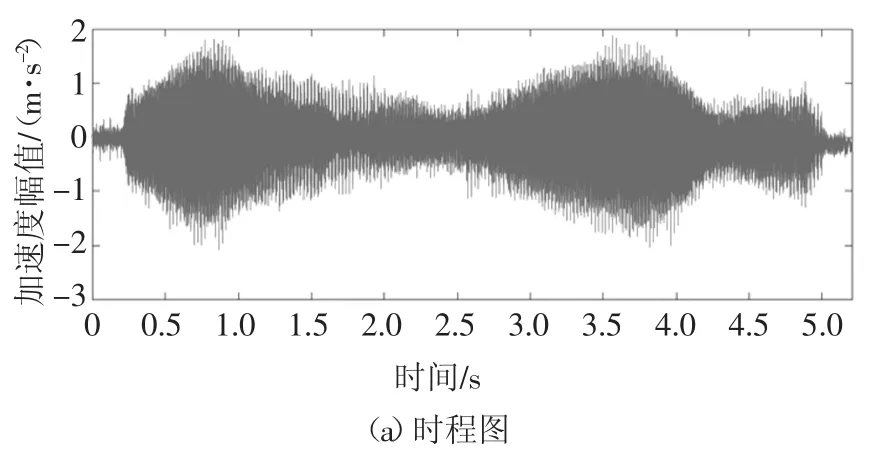
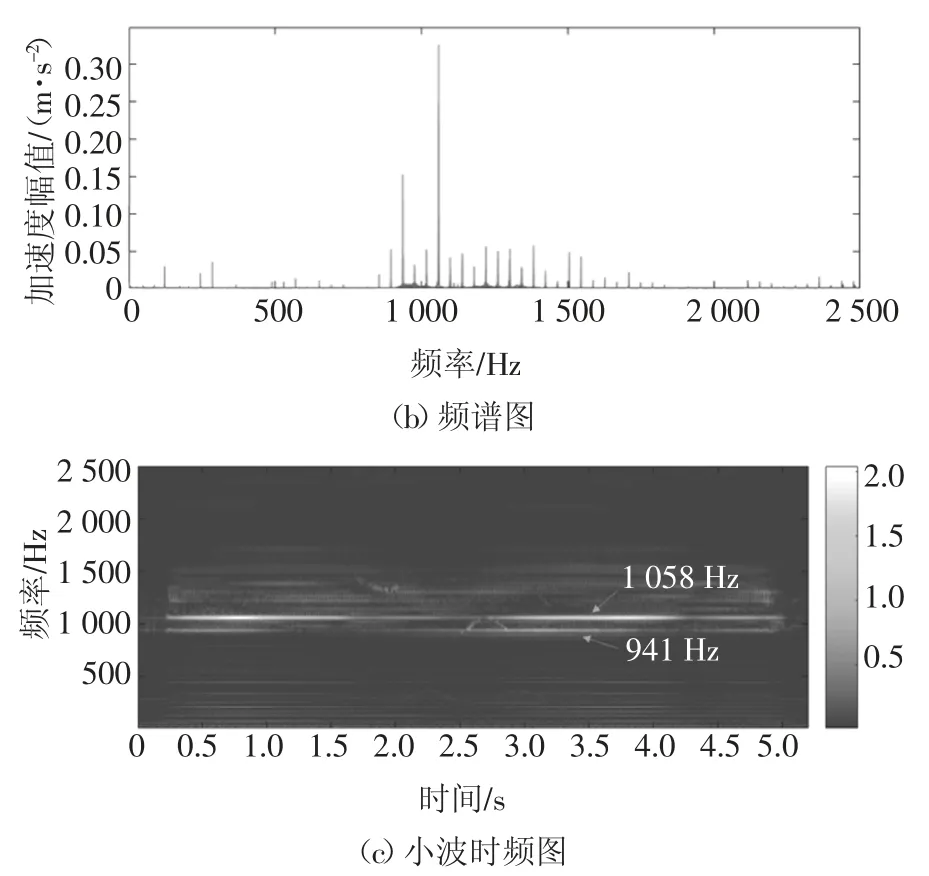
图6 采用1号实验时e号测点的时程图、频谱图和时频图Fig.6 Time history，frequency and time-frequency responses of point e in testing 1

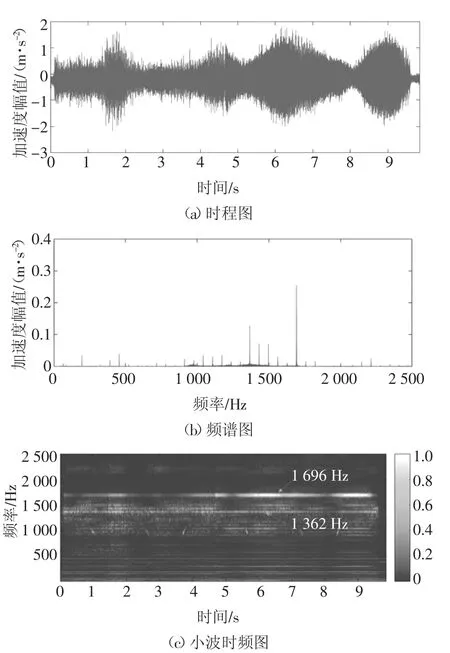
图7 采用4号实验时e号测点的时程图、频谱图和时频图Fig.7 Time history，frequency and time-frequency responses of point e in testing 4

图6中最主要的频率组成分别为941 Hz和1 058 Hz，其他频率的振幅较小.图7中最主要的频率组成是1 362 Hz和1 696 Hz，其他频率的振幅较小.再分析e～i号测点的其他数据也可以观察到类似的现象：频谱图中有2个振幅较大的高频，而其他频率的振幅较小，并且在砂轮转速相同的实验组中该高频频率相同.这一现象表明，由于e～i号测点与砂轮间的距离相对a～d号测点较远，故此时受迫振动衰减较明显，在频谱图中观察到的高频为磨床自激振动的频率，即颤振频率.在磨削过程的初期和末期出现较多高频振动，表明砂轮开始接触凸轮轴及砂轮开始脱离凸轮轴时，由于磨削面积的改变会引起颤振系统变化，加剧了颤振产生.

最后取距离砂轮位置较远的j～m号测点作为研究对象进行分析.当磨削深度为0.05 mm时，分别采用1号和4号实验，测得m号测点的数据进行频域与时频域分析.结果分别如图8和图9所示.

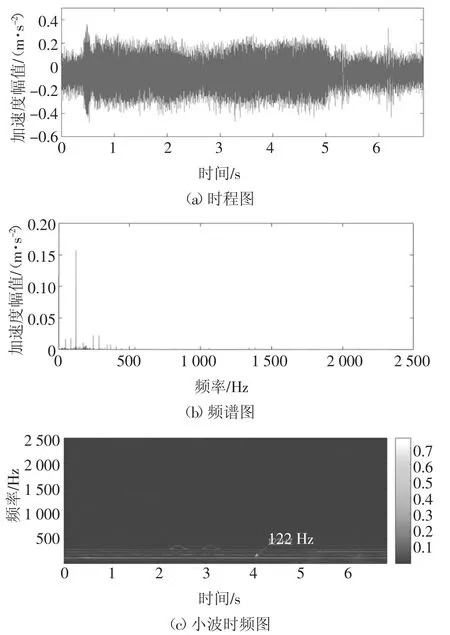
图8 采用1号实验时m号测点的时程图、频谱图和时频图Fig.8 Time history，frequency and time-frequency responses of point m in testing 1

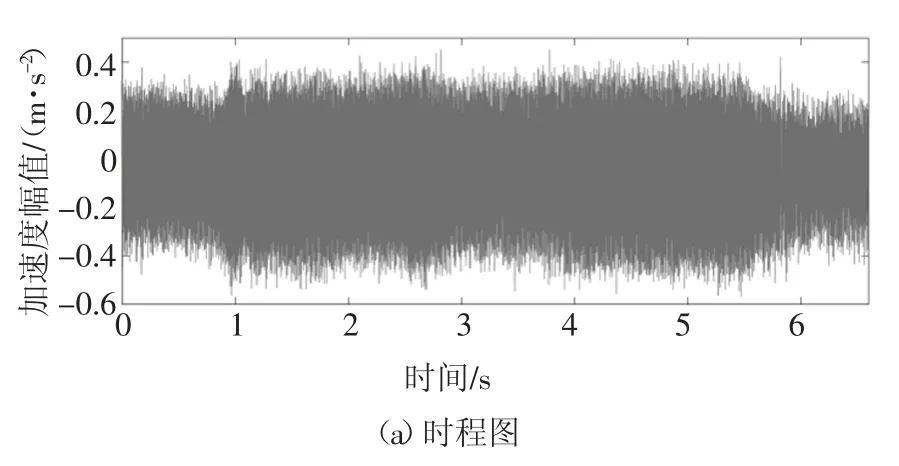
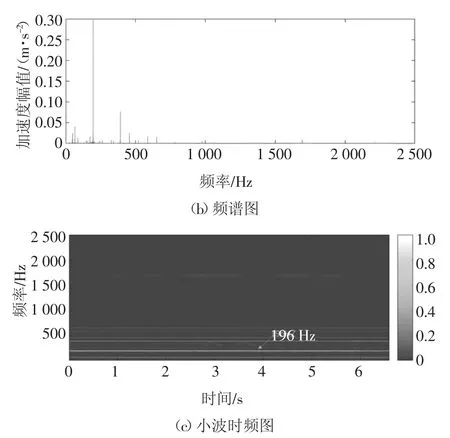
图9 采用4号实验时m号测点的时程图、频谱图和时频图Fig.9 Time history，frequency and time-frequency responses of point m in testing 4

图8中最主要的频率组成是122 Hz，其他频率的幅值较小，而此时砂轮的旋转频率约为42 Hz；图9中最主要的频率组成是196 Hz，其他频率的幅值较小，而此时砂轮的旋转频率约为66 Hz.再分析j～m号测点的其他数据也可以观察到类似的现象：在整个磨削过程中，始终出现较多较为平稳的低频振动；在砂轮转速相同的实验组中最主要的频率组成相同，且接近于砂轮的旋转频率的倍频和磨床的固有频率133 Hz.结果表明，j～m号测点距离大砂轮较远且整机刚度较大，受迫振动和自激振动都已经衰减，仅能检测到部分频率接近系统固有频率的受迫振动.

4.4 颤振稳定性预测验证

磨床的振动主要包括电机驱动主轴旋转产生的受迫振动和工件与砂轮相互作用产生的再生颤振.本文主要研究再生颤振，为了减少受迫振动对测试数据的影响，取测试方向为磨削深度方向且距离适中的e号测点数据进行分析，测试得到加速度幅值的峰值如表3所示.

当工件转速不同而砂轮转速相同时，测试得到的数据基本接近，符合绘制的稳定性极限图，数据间的差异可能是由实验误差和受迫振动的影响产生的.将实验的加工参数绘制到图2中，位于曲面下方的为稳定区，位于曲面上方的为不稳定区.可以发现处于稳定区的实验测得的加速度幅值的峰值较小，除了个别数据外都小于4 m/s2；处在不稳定区的实验测得的加速度幅值的峰值较大，全部大于4 m/s2.由此可以验证动力学模型的正确性，并可利用稳定性极限图对该磨床的颤振稳定性进行预测.

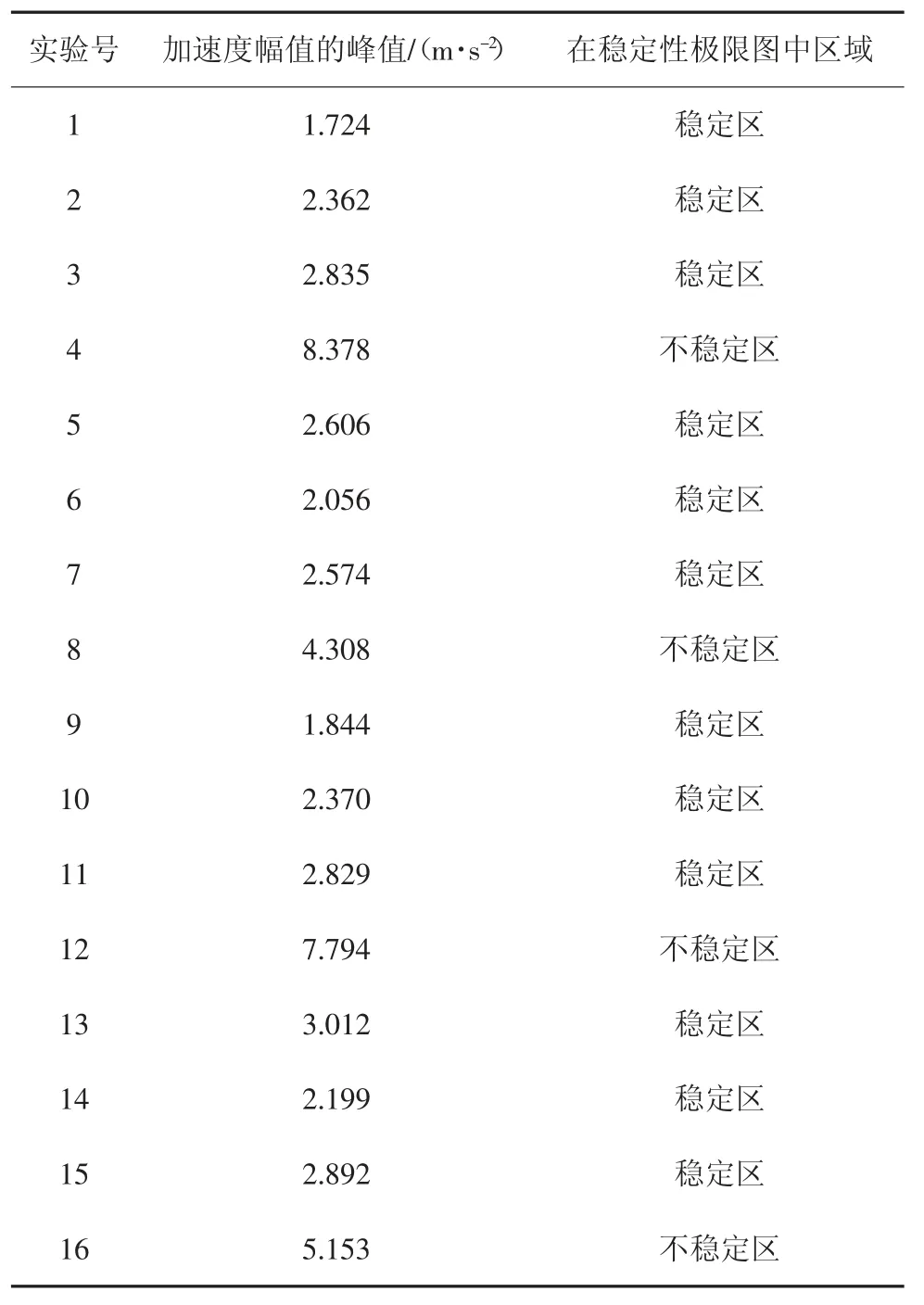
表3 测点加速度幅值的峰值和稳定性区域Tab.3 Acceleration amplitude and stability region of sensors

5 结论

本文对某随动凸轮轴磨床进行颤振实验，研究其颤振稳定性，得到如下结论：

1）针对再生型颤振对某随动凸轮轴磨床建立了磨削动力学模型，绘制了此磨床系统的稳定性极限图.

2）通过颤振实验，利用频域与时频域分析方法对实验数据进行分析，总结了磨床距离砂轮远、中、近不同位置上的振动特点及振动原因，为磨床的消振与减振设计提供依据.

3）将实验结果与稳定性极限图的预测结果进行对照，验证了磨削动力学模型和稳定性极限图的正确性，在磨床的实际加工过程中，可利用稳定性极限图进行磨削参数的优选，减少颤振产生.