双重螺旋法齿面分区修形对降低安装误差敏感性的影响

严宏志，吴顺兴，肖蒙



双重螺旋法齿面分区修形对降低安装误差敏感性的影响

严宏志1, 2，吴顺兴1, 2，肖蒙1, 2

(1. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083；2. 中南大学 机电工程学院，湖南 长沙，410083)

为了降低齿轮副对安装误差的敏感性，将双重螺旋法加工的齿面划分为小端、中间接触区和大端3个区域，并沿啮合线方向对3个区域分别进行抛物线修形，得到修形后的理论齿面；采用有约束最小二乘法求得与修形后理论齿面逼近的修形后实际齿面；通过齿轮承载接触分析(LTCA)，得到原始齿面与修形后实际齿面在有安装误差时的齿面接触区、接触应力和齿根弯曲应力。研究结果表明：经过分区修形，正、反车齿面最大接触应力降低，齿面接触应力更加均匀，齿轮副对安装误差的敏感性降低，同时，齿根弯曲应力也有一定程度增大。

双重螺旋法；安装误差敏感性；分区修形；齿轮承载接触分析

在实际工程中，螺旋锥齿轮副不可避免地存在安装误差，这将使齿轮副冲击振动与噪声增大，并导致不均匀磨损，缩短使用寿命，因此，使设计的齿轮副对安装误差具有低敏感性是齿轮研究的一个重要课题。目前，有关啮合质量对安装误差的敏感性已有较多研究。王峰等[1]开展了摆线齿准双曲面齿轮在安装误差情况下的齿轮接触分析，研究了安装误差对其啮合性能的影响；刘光磊等[2]通过分析安装误差对接触印痕位置影响确定了齿轮副安装误差的合理范围；佟操等[3]采用动力学软件ANSYS/LS-DYNA 对直齿圆柱齿轮进行动态仿真，得到了不同安装误差对应的动态接触应力；王小椿等[4]通过解析法建立了安装误差与齿面啮合特性的对应关系；LI等[5−7]采用有限元方法对直齿圆柱齿轮副进行加载接触分析，研究了安装误差对齿面接触应力、齿根弯曲应力、啮合刚度和承载传动误差等的影响；FALAH等[8]对单包络(圆柱)蜗杆传动副进行加载接触分析，研究了安装误差对接触线、负载和应力分布的影响；ZHANG等[9]通过齿轮接触分析，研究了不同安装误差对双圆弧弧齿锥齿轮啮合性能的影响。针对如何降低齿轮副啮合性能对安装误差的敏感性，目前已有一些研究；LITVIN 等[10−11]通过预置接触轨迹及传动误差曲线得到了低安装误差敏感性的齿面；SIMON等[12−13]对弧齿锥齿轮副进行加载接触分析，通过优化的小轮机床加工参数降低了齿轮副对安装误差的敏感性；苏进展等[14−15]提出了通过优化差曲面全曲率来降低弧齿锥齿轮安装误差敏感性的方法，同时提出了齿面的低敏感性修形方法，但是其针对的只是工作齿面的修形；王会良等[16]通过对斜齿轮的齿廓和齿向进行分段修形，降低了其对安装误差的敏感性；曹雪梅等[17]以齿廓、齿向修形系数为优化变量，通过对主动轮进行鼓形修形，从而降低了齿轮副对安装误差的敏感性。上述研究为双重螺旋法加工的螺旋锥齿轮副面向安装误差敏感性修形提供了参考，但是，基于双重螺旋法的螺旋锥齿轮加工具有正车面和反车面两面同时加工、两面同时修形的特点，为此，本文作者针对具有双面综合优化的分区修形方法和机床调整参数修正方法进行研究。

1 安装误差低敏感性分区修形

螺旋锥齿轮齿面的大端和小端修形可减小由安装误差带来的接触区位置、大小和形状以及接触应力的变化程度，从而降低齿轮副对安装误差的敏感性。以接触区的边界作为分界线将齿面分成3部分即小端、中间接触区和大端。沿啮合线方向进行3段抛物线修形，小端、中间接触区和大端分别对应1段抛物线。图1所示为齿面分区示意图。

以啮合线与接触迹线的交点为坐标原点，齿面法线方向为方向，指向轮齿大端的啮合线方向为方向，建立抛物线修形坐标系，如图2所示(其中，为预置的瞬时接触椭圆长半轴的长度)。

图1 齿面分区示意图

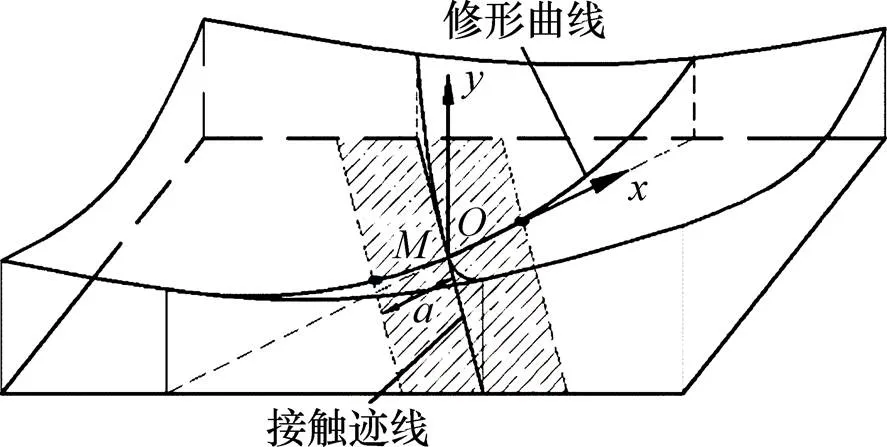
图2 抛物线修形坐标系

图3所示为抛物线修形曲线。其中，抛物线Ⅰ，Ⅱ和Ⅲ分别为沿啮合线方向在齿面接触区内，小端区域内和大端区域内的修形曲线；0，1和2分别为接触区边界上的修形量，小端给定的最大修形量和大端给定的最大修形量；1和2在数值上等于预设的接触椭圆长半轴的长度，3和4分别为靠近小端和大端齿面区域内沿轴到接触迹线的最远距离。

沿啮合线方向3段抛物线修形曲线的表达式为

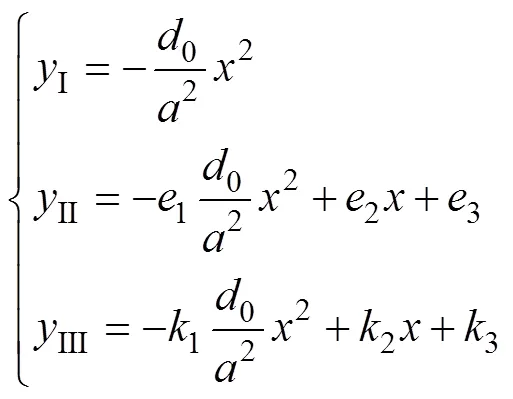
式中：1，2和3为抛物线II的修形系数；1，2和3为抛物线III的修形系数。

要保证3段抛物线连续可导，应该满足如下约束条件：

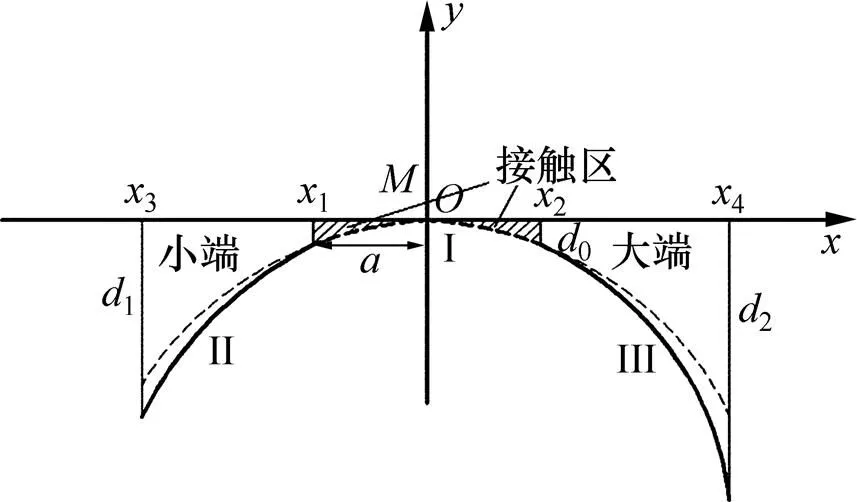
图3 抛物线修形曲线

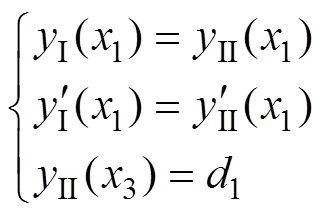
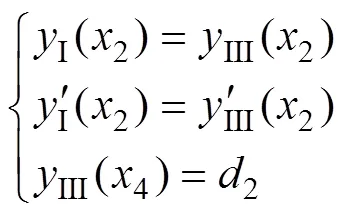
沿啮合线方向的法向修形量为

将齿面离散为45个网格点，求得各个离散点的法向修行量，以各个离散点的法向修行量作为小轮原始齿面与修形后理论齿面的法向偏差值。

2 小轮加工参数求解

齿面偏差的产生有很多原因，通过修正机床调整参数可以最大限度地实现齿面偏差的最小化。

原始齿面和修形后理论齿面的偏差可表示为

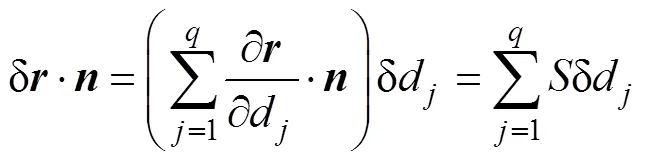
采用双重螺旋法加工时，1组机床调整参数同时加工正车面和反车面，第个网格点对应第个机床调整参数，敏感系数矩阵可表示为

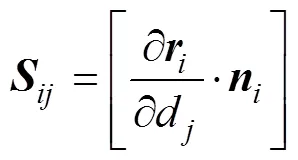
式中：=1，2，…，；=1，2，…，。

令为第个网格点的齿面偏差，则有

式中：为正车面和反车面的所有网格点的齿面偏差矩阵；为对应所有网格点的敏感系数矩阵；Δ为机床调整参数修正值矩阵。

由于机床调整参数的数目小于齿面网格点的数目，故式(7)为超静定方程线性方程组，因此，采用约束最小二乘法求解。对于每1个选用的修正参量，根据使用的机床类型以及齿面偏差给出1个合适的范围，即可求得理想的机床调整参数修正值。

3 算例分析

以1对大轮采用成形法、小轮采用双重螺旋法加工的准双曲面齿轮副为例，轮坯参数见表1，小轮的原始齿面加工参数见表2，2组修形参数见表3。

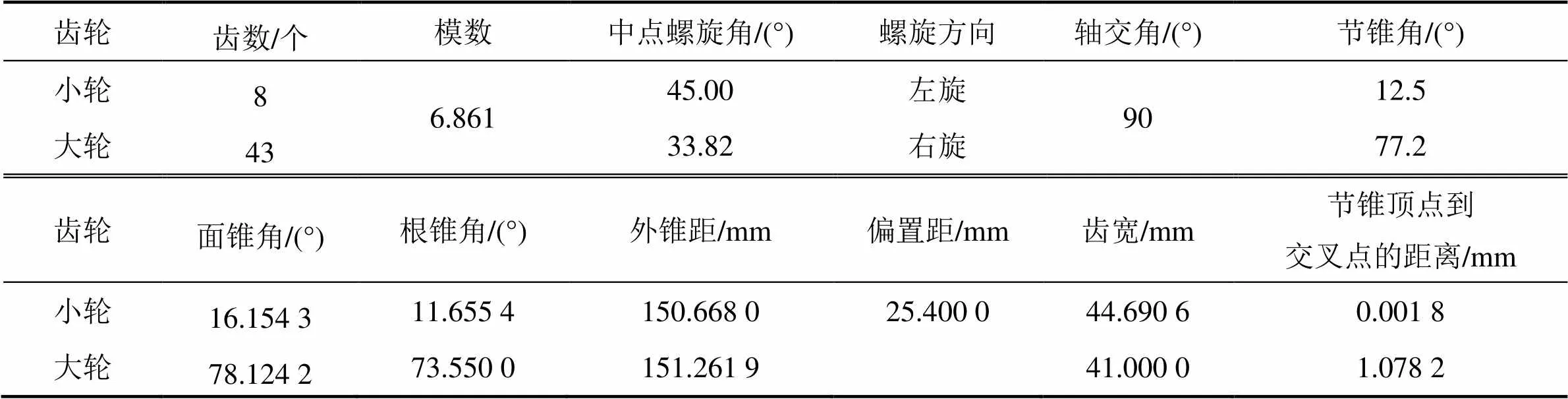
表1 轮坯参数

表2 原始齿面小轮加工参数

表3 修形参数

由表3中的修形参数1和修形参数2分别得到修形后理论齿面1和修形后理论齿面2。图4和图5所示分别为修形后理论齿面1和修形后理论齿面2与原始齿面的偏差图。利用有约束最小二乘法对原始齿面进行修正，得到满足修形后理论齿面的小轮加工参数，如表4所示。通过表4中修形后的小轮加工参数分别得到对应修形参数1和修形参数2的修形后实际齿面1和修形后实际齿面2。图6和图7所示分别为修形后实际齿面1和修形后实际齿面2和原始齿面的偏差图。

从图4~7可见：修形后理论齿面和修形后实际齿面基本保证了正车面和反车面的中间接触区不变，而在大端和小端沿啮合线方向有一定的修形量。对比修形后理论齿面和修形后实际齿面的正车面和反车面可知：修形后实际齿面与修形后理论齿面接近，说明采用有约束最小二乘法求得的小轮两面同时加工的机床调整参数符合设计要求。

图4 修形后理论齿面1和原始齿面的偏差图

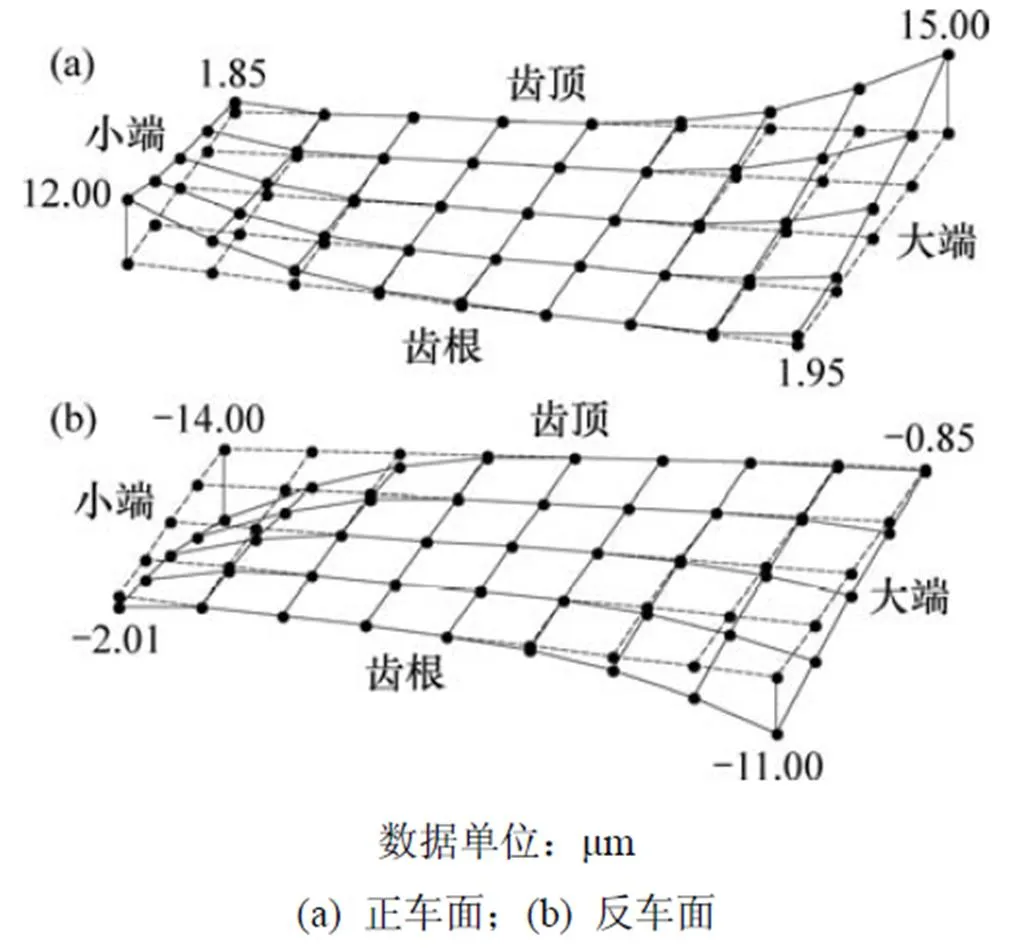
图5 修形后理论齿面2和原始齿面的偏差图

齿轮副进行分区修形后，对其进行齿轮承载接触有限元分析。小轮轴向安装误差0 mm，大轮轴向安装误差=−0.16 mm，小轮偏置距误差−0.15 mm。给定载荷600 N∙m时，对比分析修形前后齿轮副在加载条件下齿面接触区、接触应力及齿根弯曲应力的变化情况。以模型中第3对齿轮为例，建立齿轮承载接触分析(LTCA)有限元模型，如图8所示。

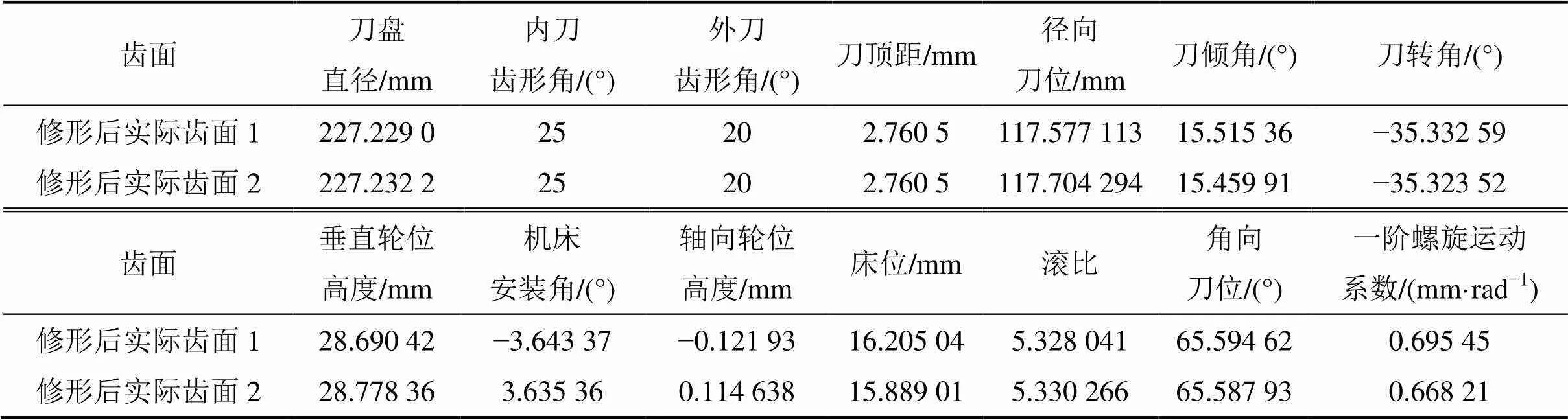
表4 修形后小轮加工参数

图9~10分别为在有安装误差情况下，通过LTCA有限元分析得到的原始齿面与修形后实际齿面的大轮正车面和反车面的接触区及接触区应力云图。由图9可见：在有安装误差情况下，原始齿面的正车面接触区完全拓展到大轮小端边界，齿面高应力区主要分布于齿顶上部。经过安装误差低敏性分区修形后，正车面接触区优化效果明显：1) 原始齿面接触区、修形后实际齿面1和修形后实际齿面2距离大轮小端的距离分别为0.154，1.179和1.697 mm，避免了小端边界接触；2) 齿面接触应力分布较为均匀，避免了高应力区主要分布在强度较小的齿顶上部；3) 最大接触应力有所减少，原始齿面的最大接触应力数值为1 289 MPa，而修形后实际齿面1和修形后实际齿面2的最大接触应力分别为1 281和1 263 MPa。

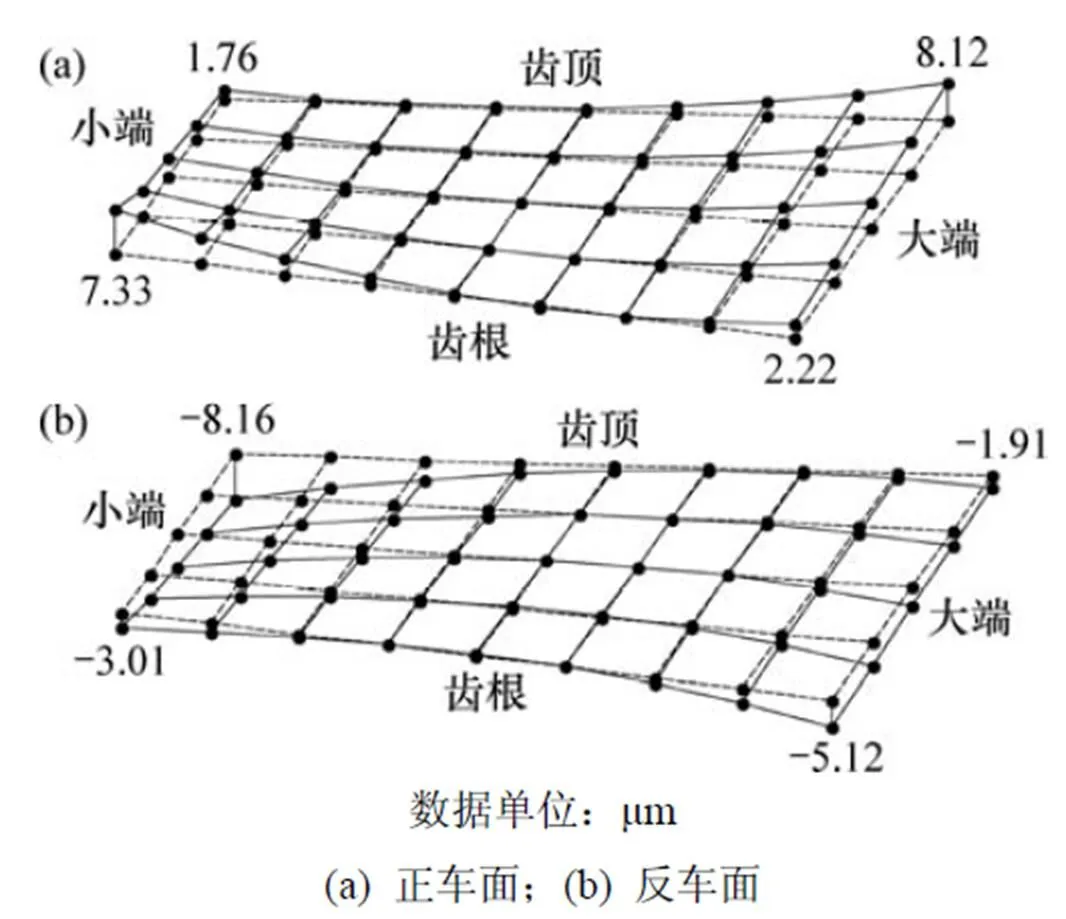
图6 修形后实际齿面1和原始齿面的偏差图

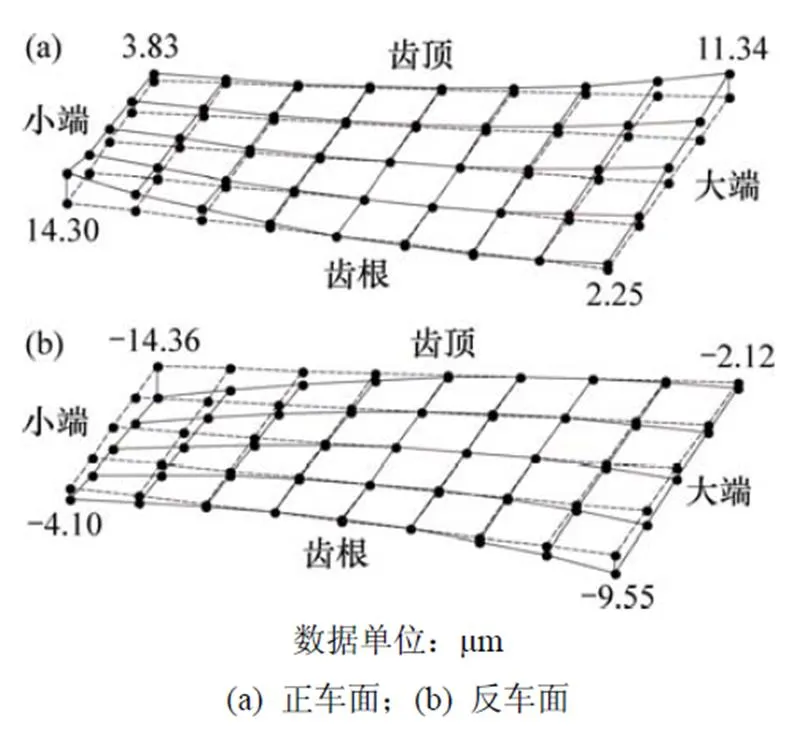
图7 修形后实际齿面2和原始齿面的偏差图

图8 LTCA有限元模型

由图10可见：原始齿面的反车面接触区基本位于齿面中间，齿根部位有向大端延伸的趋势，经过安装误差低敏感性分区修形后，反车面接触区优化效果较好：1) 齿根部位向大端延伸的趋势稍减，原始齿面接触区、修形后实际齿面1和修形后实际齿面2与大轮小端的距离分别为5.689，5.791和6.304 mm；2) 最大接触应力有所减少，原始齿面的最大接触应力为1 406 MPa，而修形后实际齿面1和修形后实际齿面2的最大接触应力分别为1 394 MPa和1 390 MPa。

(a) 原始齿面；(b) 修形后实际齿面1；(c) 修形后实际齿面2

对比图9和图10可知：修形后实际齿面2的优化效果优于修形后实际齿面1的优化效果，说明从齿面接触应力及接触区的优化角度来说，适当增大大端和小端的修形量也可以提高正车面和反车面的优化效果，降低齿轮副对安装误差的敏感性。

齿轮弯曲应力反映齿轮齿根部位抗疲劳折断的能力，根据第3强度理论，通过有限元软件对小轮原始齿面和修形后实际齿面的齿根弯曲应力进行分析，分别得到小轮正车面和反车面的齿根弯曲应力云图，如图11和图12所示。

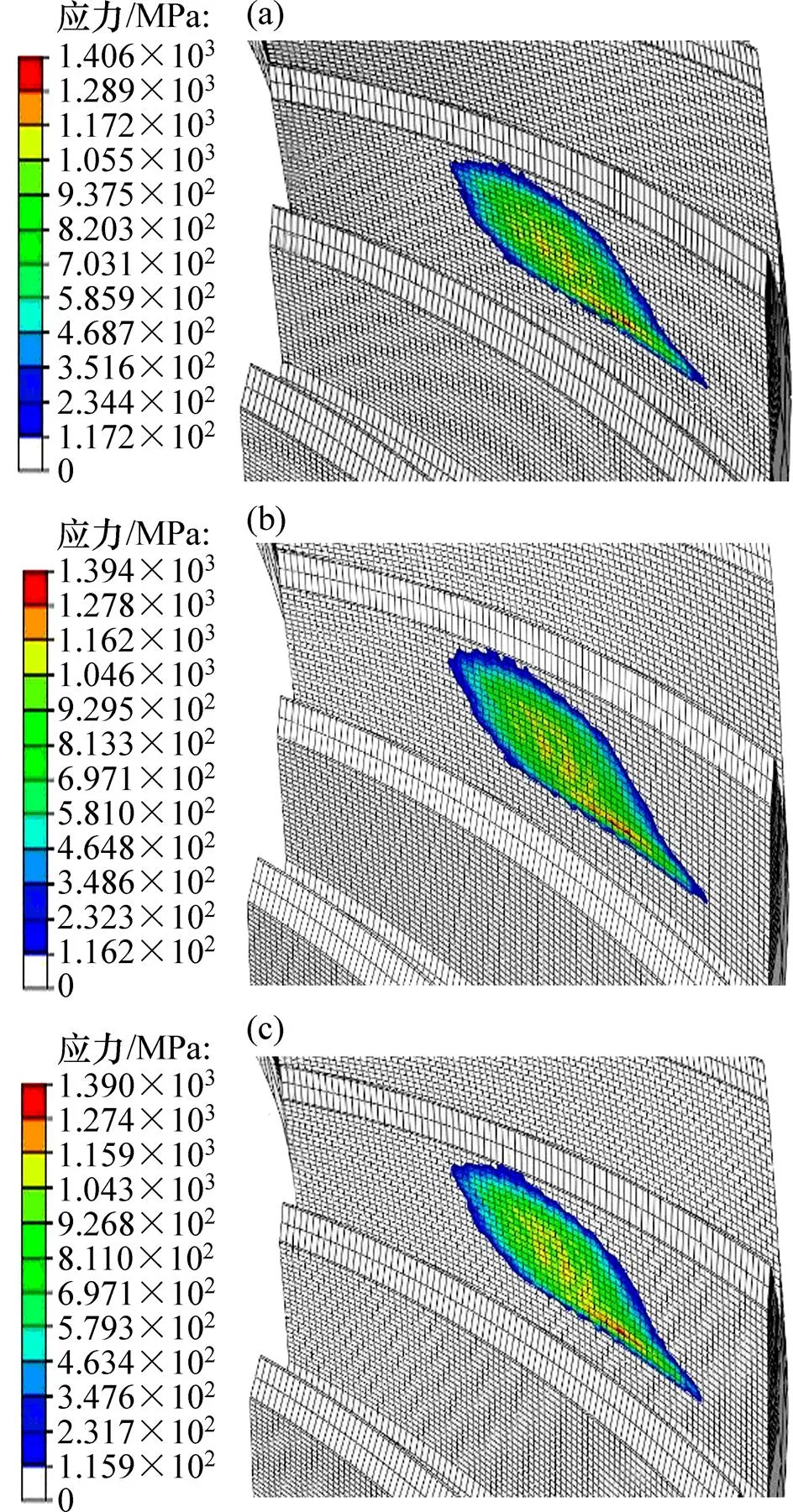
(a) 原始齿面；(b) 修形后实际齿面1；(c) 修形后实际齿面2

由图11和图12可知：原始齿面正车面的齿根最大弯曲应力为106.182 MPa，反车面的齿根最大弯曲应力为86.662 MPa；修形后实际齿面1正车面的齿根最大弯曲应力为106.897 MPa，反车面的齿根最大弯曲应力为87.162 MPa；修形后实际齿面2正车面的齿根最大弯曲应力为107.537 MPa，反车面的齿根最大弯曲应力为87.523 MPa。说明随着大端和小端的修形量增加，齿厚减小，齿根弯曲应力有所增大。所以，修形量的确定需要综合齿面接触情况和齿轮强度，同时考虑实际工况条件来确定。

(a) 原始齿面；(b) 修形后实际齿面1；(c) 修形后实际齿面2

4 实验验证

采用由哈量集团研发生产的H650C数控螺旋锥齿轮铣齿机加工实验所用齿轮，在加工好的齿轮齿面上涂上红丹粉，并在YDX9550锥齿轮滚动检查机上进行滚检实验，验证基于双重螺旋法加工的齿面分区修形方法对降低安装误差敏感性的有效性以及仿真分析结果的正确性。

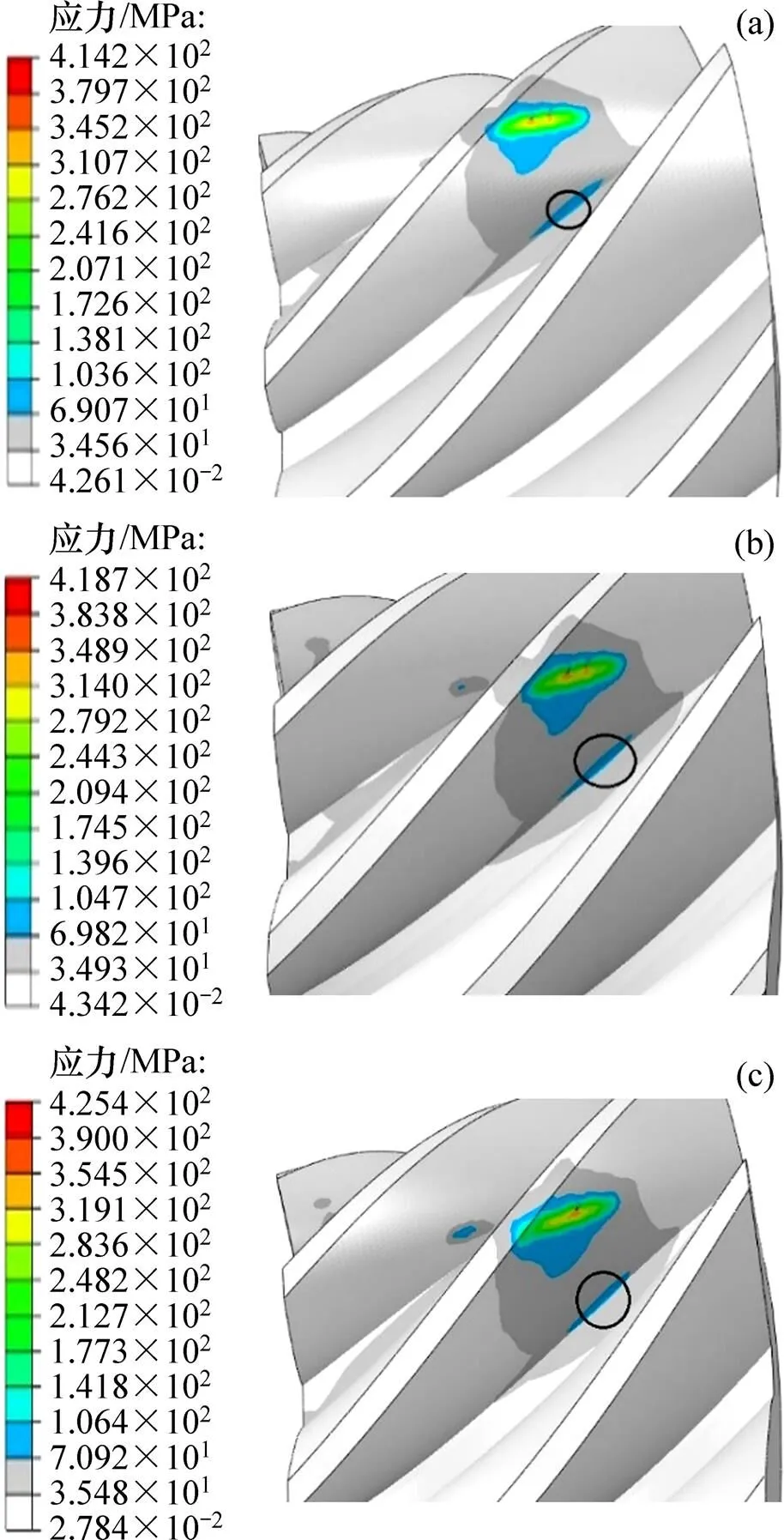
(a) 原始齿面；(b) 修形后实际齿面1；(c) 修形后实际齿面2

由于修形方法原理相似，同时考虑到加工成本和时间，实验只对1组修形参数进行验证，即验证由第2组修形参数得到的齿面。此外，由于实验条件限制，滚检机是在负载为20 N∙m条件下进行的，原始齿面和修形后实际齿面2的正车面接触区及反车面接触区分别如图13和图14所示。

由图13可见：原始齿面与修形后实际齿面2的大轮正车面的接触区位置和啮合方向与仿真结果基本相似；原始齿面与修形后实际齿面2的接触区形状有微小差别，其中原始齿面的接触区有明显的向轮齿小端齿根延伸的一段狭窄区域，而修形后实际齿面2的接触区更加规则，向小端齿根延伸的程度较小。由图14可见：原始齿面与修形后实际齿面2的大轮反车面接触区变化不明显，没有正车面的修形优化效果明显，但经过修形后齿面的接触区向大端延伸的范围比原始齿面的小。

(a) 原始齿面；(b) 修形后实际齿面2

(a) 原始齿面；(b) 修形后实际齿面2

对比实验结果可知：原始齿面与修形后实际齿面2接触区形状存在差异，说明齿面修形能够有效降低齿轮副对安装误差的敏感性，避免了在实际工况中由于偏离理论安装位置而出现大、小端接触或者齿根、齿顶接触的情况。

5 结论

1) 建立双重螺旋法小轮双面3段修形模型，并在误差敏感矩阵基础上，采用有约束最小二乘法对修形后的机床调整参数进行求解，求解的机床调整参数符合设计要求。

2) 修形后，正车面和反车面齿面最大接触应力减小，接触应力分布更均匀，避免了齿顶高应力接触，提高了齿轮啮合稳定性。

[1] 王峰, 方宗德, 李声晋, 等. 考虑安装误差的摆线齿准双曲面齿轮轮齿接触分析[J]. 农业机械学报, 2012, 43(9): 213−218. WANG Feng, FANG Zongde, LI Shengjin, et al. Tooth contact analysis of epicycloid hypoid gear considering assembly misalignment[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(9): 213−218.

[2] 刘光磊, 张瑞庭, 赵宁, 等. 一种弧齿锥齿轮安装误差变动范围的确定方法[J]. 机械工程学报, 2014, 48(3): 34−40. LIU Guanglei, ZHANG Ruiting, ZHAO Ning, et al. An approach to determine installation errors of spiral bevel gears[J]. Chinese Journal of Mechanical Engineering, 2014, 48(3): 34−40.

[3] 佟操, 孙志礼, 马小英, 等. 考虑安装与制造误差的齿轮动态接触仿真[J]. 东北大学学报(自然科学版), 2014, 35(7): 996−1000. TONG Cao, SUN Zhili, MA Xiaoying, et al. Dynamic simulation of spur gears with assembly errors and machining errors[J]. Journal of Northeastern University(Natural Science), 2014, 35(7): 996−1000.

[4] 王小椿, 吴序堂. 空间点啮合齿面的接触特性对安装误差的敏感性分析[J]. 西安交通大学学报, 1990, 24(6): 45−58. WANG Xiaochun, WU Xutang. Sensitivity of the contact characteristics of skew point contact surfaces to the mounting errors[J]. Journal of Xi’an Jiaotong University, 1990, 24(6): 45−58.

[5] LI Shuting. Effects of machining errors, assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears[J]. Mechanism & Machine Theory, 2007, 42(6): 698−726.

[6] LI Shuting. Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors, assembly errors and tooth modifications[J]. Mechanism & Machine Theory, 2007, 42(1): 88−114.

[7] LI Shuting. Effects of misalignment error, tooth modifications and transmitted torque on tooth engagements of a pair of spur gears[J]. Mechanism & Machine Theory, 2015, 83: 125−136.

[8] FALAH A H, ALFARES M A, ELKHOLY A H. Localised tooth contact analysis of single envelope worm gears with assembly errors[J]. International Journal of Advanced Manufacturing Technology, 2013, 68(9/10/11/12): 2057−2070.

[9] ZHANG Ruiling, WANG Tie. The influences of installation errors on double circular arc tooth spiral bevel gear using TCA method[J]. Journal of Convergence Information Technology, 2012, 7(1): 1−10.

[10] LITVIN F L, FUENTES A, HAYASAKA K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears[J]. Mechanism & Machine Theory, 2006, 41(1): 83−118.

[11] ARGYRIS J, FUENTES A, LITVIN F L. Computerized integrated approach for design and stress analysis of spiral bevel gears[J]. Computer Methods in Applied Mechanics & Engineering, 2002, 191(11): 1057−1095.

[12] SIMON V V. Machine-tool settings to reduce the sensitivity of spiral bevel gears to tooth errors and misalignments[J]. Journal of Mechanical Design, 2008, 130(8): 082603-1−082603-10.

[13] SIMON V V. Influence of tooth errors and misalignments on tooth contact in spiral bevel gears[J]. Mechanism & Machine Theory, 2008，43(10): 1253−1267.

[14] 苏进展, 方宗德. 弧齿锥齿轮误差敏感性优化设计[J]. 航空动力学报, 2012 , 27(1): 181−189. SU Jinzhan, FANG Zongde. Optimization design of the error sensitivity for spiral bevel gears[J]. Journal of Aerospace Power, 2012, 27(1): 183−189.

[15] 苏进展, 方宗德.弧齿锥齿轮低敏感性修形[J]. 航空动力学报, 2012, 27(8): 1895−1901. SU Jinzhan, FANG Zongde. Low sensitivity modification for spiral bevel gears[J]. Journal of Aerospace Power, 2012, 27(8): 1895−1901.

[16] 王会良, 邓效忠, 徐凯, 等. 考虑安装误差的拓扑修形斜齿轮承载接触分析[J]. 西北工业大学学报, 2014, 32(5): 781−786. WANG Huiliang, DENG Xiaozhong, XU Kai, et al. Load tooth contact analysis(LTCA) of helical gears using topographic modification and installation errors[J]. Journal of Northwestern Polytechnical University, 2014, 32(5): 781−786.

[17] 曹雪梅, 孙宁, 邓效忠. 直齿锥齿轮低安装误差敏感性设计与实验验证[J]. 航空动力学报, 2016, 31(1): 227−232. CAO Xuemei, SUN Ning, DENG Xiaozhong. Design for straight bevel gear based on low installation error sensitivity and experiment tests[J]. Journal of Aerospace Power, 2016, 31(1): 227–232.

Effect of tooth surface zoning modification by duplex helical method on reducing sensitivity of installation error

YAN Hongzhi1, 2, WU Shunxing1, 2, XIAO Meng1, 2

(1. State Key Laboratory for High Performance Complex Manufacturing, Central South University, Changsha 410083, China; 2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

To reduce the sensitivity of the gear pair to the installation error, the original tooth surface generated by duplex helical method was divided into three regions, i.e. the toe region, the middle region and the heel region. Modifications of these regions with three parabolic segments were conducted along the meshing line, and then theoretical tooth surfaces were obtained. Theconstraint least square method was used to minimize the tooth flank form error between the theoretical modified tooth surface and the actual modified tooth surface. Then, the contact area, the contact stress, the bending stress of tooth root of the original tooth surface and the actual modified tooth surface in the presence of installation error were obtained by loaded tooth contact analysis (LTCA). The results show that the maximum contact stress of the drive side and the coast side are both reduced by zoning modification. Meanwhile, the tooth surface contact stress is more uniform. Thus, sensitivity of installation error of gear pair is reduced and the bending stress of the root increases to a certain extent.

duplex helical method; installation error sensitivity; zoning modification; loaded tooth contact analysis

10.11817/j.issn.1672−7207.2019.02.006

TH132.41

A

1672−7207(2019)02−0286−09

2018−04−05；

2018−06−25

国家自然科学基金资助项目(51575533)(Project(51575533) supported by the National Natural Science Foundation of China)

严宏志，博士，教授，从事复杂曲面数字制造理论与技术研究；E-mail：yhzcsu@163.com

(编辑 伍锦花)