考虑尺度效应具损伤微板的坍塌特性分析

袁集海，张祥敏，陈昌萍†

（1.厦门大学 建筑与土木工程学院，福建 厦门361005；2.厦门理工学院 土木工程与建筑学院，福建 厦门361024）

微机电系统（MEMS）因其优越的性能而被广泛应用于通讯、航空航天、生物医学等领域.微板结构是MEMS中主要的结构之一，其主要应用于微泵、微镜和微麦克风等.然而，MEMS微板尺寸微小，在工作的过程中抵抗外界因素如：温度[1]、湿度[2]和微结构之间的微观力[3-4]影响的能力较差，微板结构会与固定极板发生吸合现象，简称坍塌（Pull-in）[5].近年来国内外学者对微结构的坍塌现象进行了研究并取得了一定的成果.陈昌萍等[6]研究了压电层合微梁的静力坍塌特性，并分析了控制电压对坍塌电压的影响.Sadeghian等[7]采用微分求积法和伽辽金法对夹支梁的坍塌不稳定性进行了分析和对比.考虑几何非线性，Ghayesh等[8]和Farokhi等[9]研究了静力驱动微板结构微机电系统的坍塌特性和非线性动力特性.基于修正偶应力理论，Kazemi等[10]研究了层合压电微板的非线性坍塌不稳定性.

以上研究主要基于经典弹性理论，研究表明微结构具有尺度效应[11].另外，MEMS器件在恶劣的环境下工作也会出现结构损伤，而目前以具损伤微板结构为对象的研究成果很少见.本文以具损伤弹性微板为研究对象，讨论了尺度效应、边缘场效应等因素对微板坍塌电压的影响.

1 基本方程

根据Yang等[12]提出的修正偶应力理论，应变能可用应力和偶应力表示为：

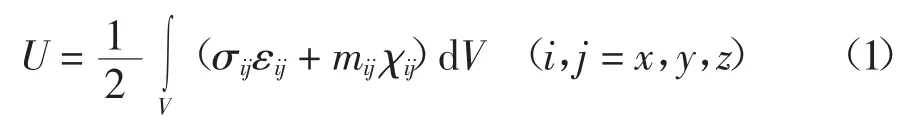
式中：σij、mij分别为应力张量和偶应力张量；εij、χij分别为应变张量和旋转梯度张量.分别定义为：

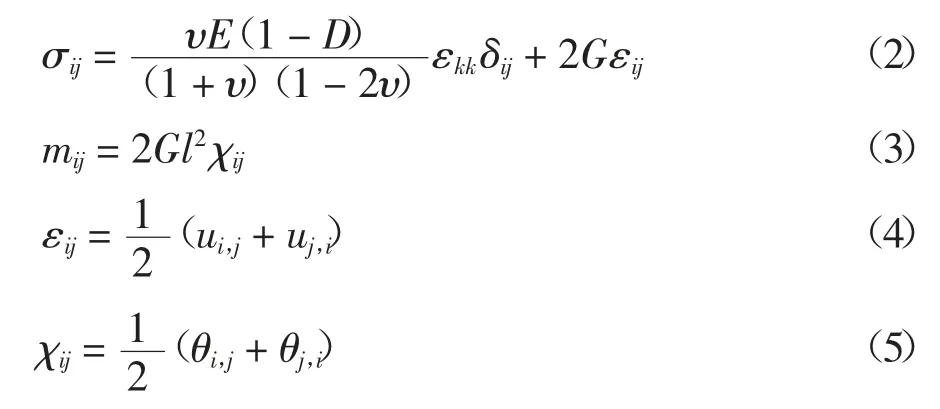
式中：i、j、k=x或y；ui为位移分量；δij为克罗内克尔符号；E、G、υ分别为弹性模量、剪切模量和泊松比；l为特征尺度参数；D为损伤变量[13]；θi为转动矢量且表示为：

式中：eijk为置换符号.

考虑如图1所示直角坐标系oxyz下的弹性微板，微板中点为坐标系原点，其长度为2a，宽度为2b，厚度为h，密度为ρ，初始时刻微板与基底之间的距离为d，且两者之间的电势差Vc，参考平面取为微板中面z=0.

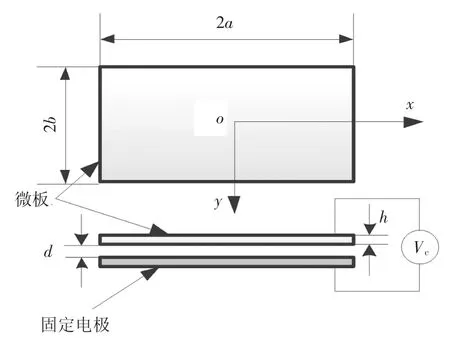
图1 微板模型Fig.1 Schematic of the micro-plate

不考虑几何非线性，由Kirchhoff假设，微板任意一点的位移u1、u2、u3可分别表示为：

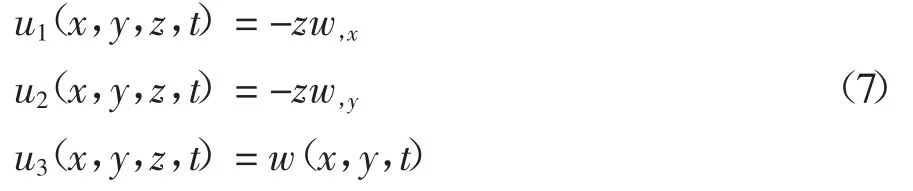
式中：w（x，y，t）为微板挠度.将式（7）代入式（4）（5）可以得到应变分量和旋转梯度分量：

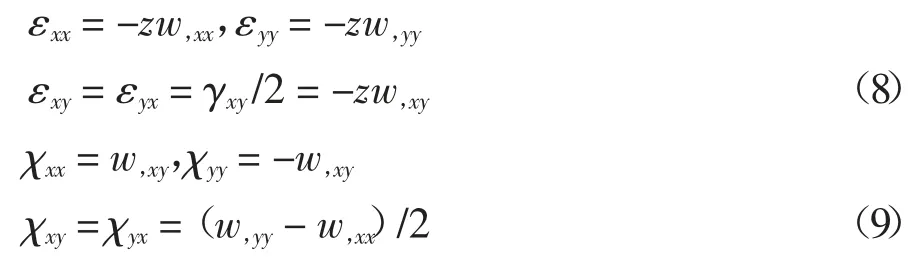
由应力和偶应力引起的弯矩分量为：

用挠度表示为：

式中：D0、Dl分别为传统弯曲刚度和旋转梯度对弯曲刚度的贡献.分别表示为：

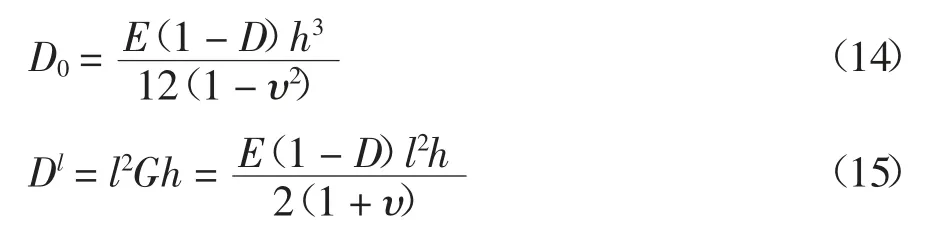
根据Hamilton原理，得

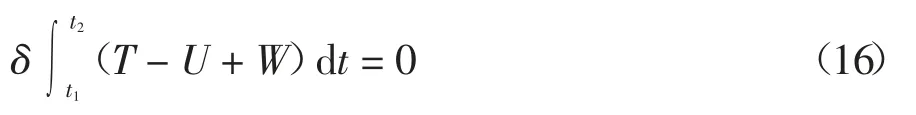
式中：T、U、W分别为系统的动能、应变能和外力所做的功.且

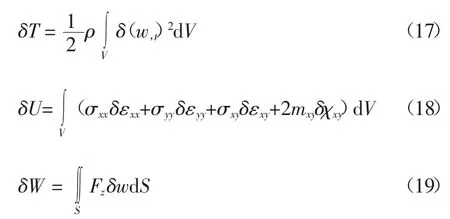
式中：Fz为电场力（考虑边缘场效应），且

将式（17）～（19）代入式（16）可得到微板的动力学方程为：

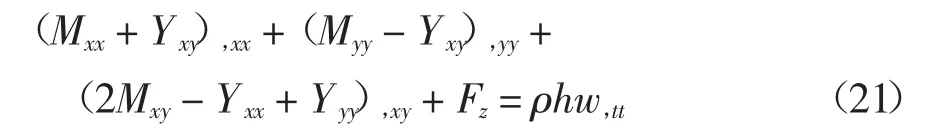
相应的边界条件为：

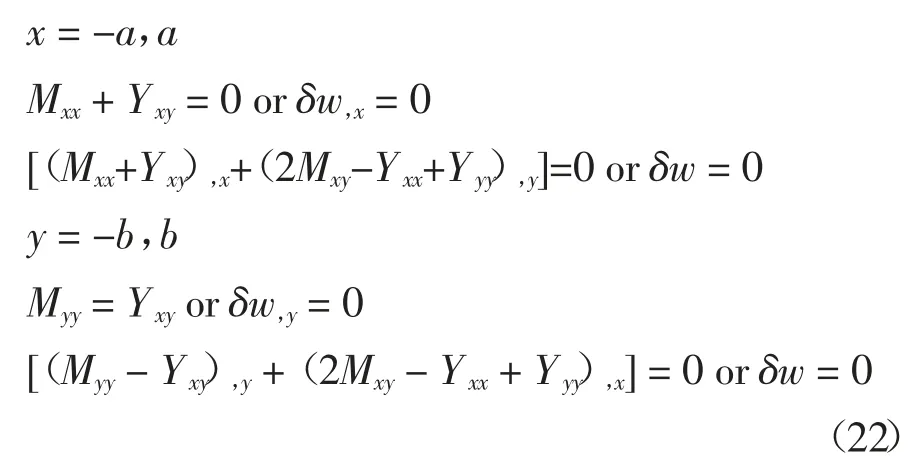
将弯矩表达式（12）（13）代入式（21）可得到用挠度表示的运动方程为：

引入下列无量纲参数：

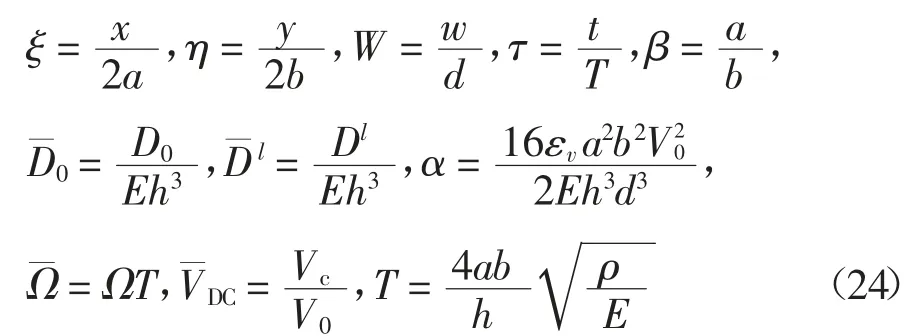
式中：V0为单位电压.

采用泰勒级数展开对电场力进行处理并保留前8项，将处理后的电场力代入运动方程并进行无量纲化.

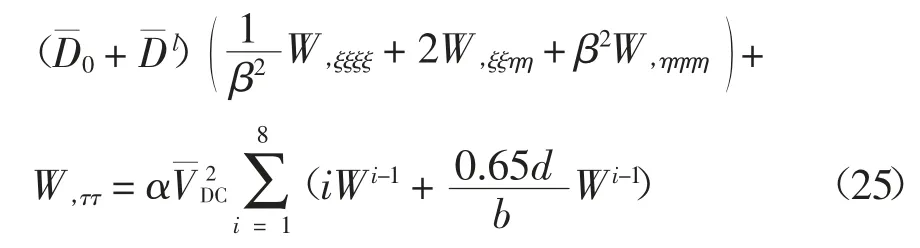
MEMS结构广泛采用夹支边界[14]，本文采用四边夹支矩形微板，其无量纲边界条件为：

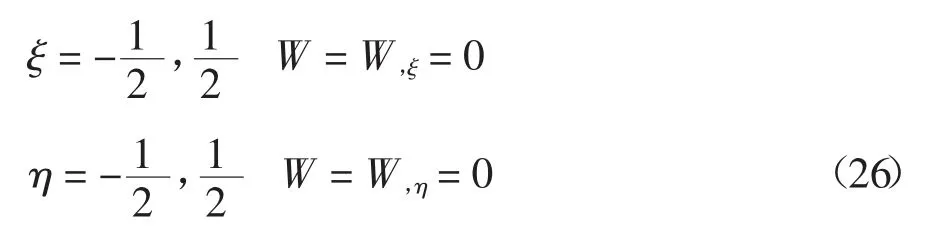
假设方程（25）满足边界条件（26）的解为：

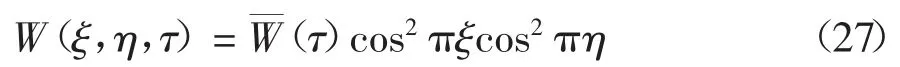
对方程（25）进行伽辽金积分可得无量纲形式常微分动力学方程.

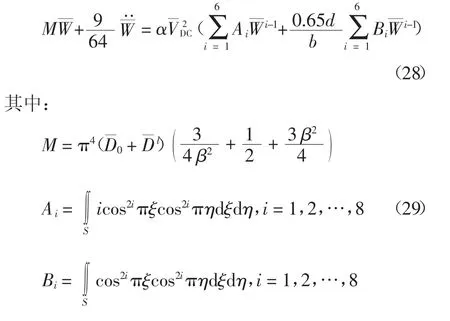
2 结果与讨论

若没有特殊说明，算例中的几何参数和物理参数如表1[15]所示.本文仅研究静力坍塌，忽略动力项后运动方程为：

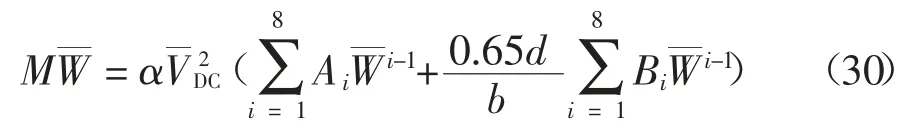
表1 微板几何参数和物理参数Tab.1 Geometric and material properties of the micro-plate

为了验证本文计算方法的合理性，在不考虑损伤和尺度效应的情况下，将本文计算结果与文献进行对比，对比结果如图2所示.从图2中可以看出，文献[15]的结果和文献[16]的实验结果与本文结果吻合得较好，说明本文的计算方法是可靠的.

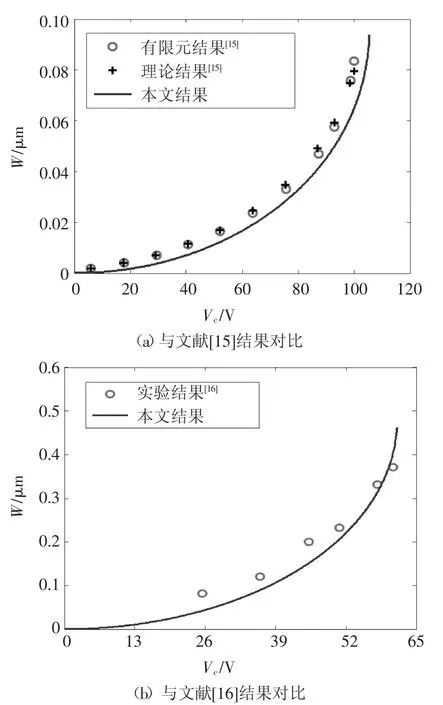
图2 本文结果与文献结果对比Fig.2 Comparison of results between present and literatures

图3给出了损伤效应对板中点挠度和坍塌电压的影响.其中，图3（a）给出了不同损伤变量对挠度电压曲线的影响（l/h=0.5）；图3（b）给出了特征尺度参数l/h=0.5（本文模型）和l/h=0（经典模型）时损伤变量对坍塌电压的影响.从图3（a）可知，随着外电压的增大，板中点挠度也不断增大；当外电压达到坍塌电压时，结构发生坍塌现象.从图3（b）可以看出，损伤变量增大，坍塌电压减小.损伤会导致结构刚度减小，结构抵抗变形能力变弱，因此坍塌电压会随损伤变量增大而减小.根据坍塌电压的变化可以从一定程度上识别微板损伤.

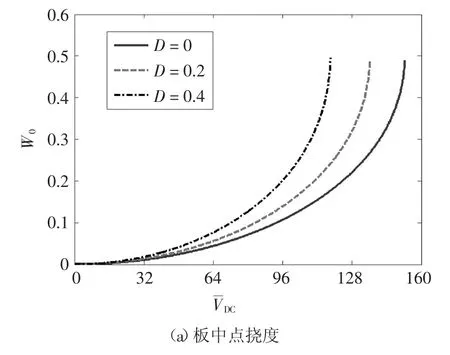
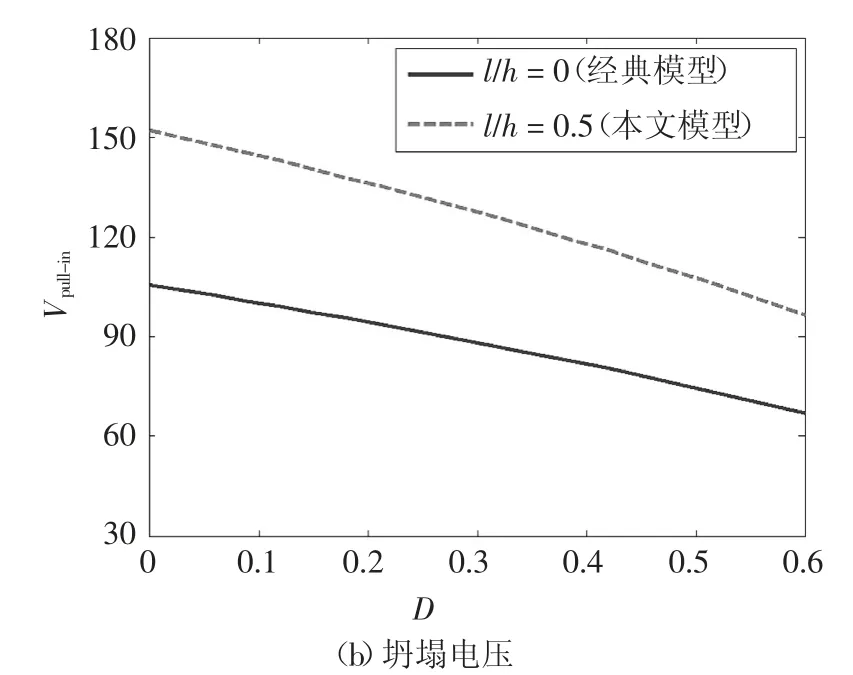
图3 损伤效应对板中点挠度和坍塌电压的影响Fig.3 Damage effect on center deflection and pull-in voltage

图4给出了尺度效应对板中点挠度和坍塌电压的影响.其中，图4（a）为不同特征尺度参数对挠度电压曲线的影响（D=0.5）；图4（b）为损伤变量D=0.2时本文模型和经典模型（l/h=0）坍塌电压随特征尺度参数变化曲线.从图4可以看出，尺度参数变大，坍塌电压也会增大.与损伤效应相反，尺度效应的存在会增加微板结构的刚度，微板结构抵抗变形的能力增强，因此坍塌电压增大.基于以上分析可知，尺度效应是不可忽视的，尤其是当微板厚度较小的时候，微板厚度越小，尺度效应越明显.

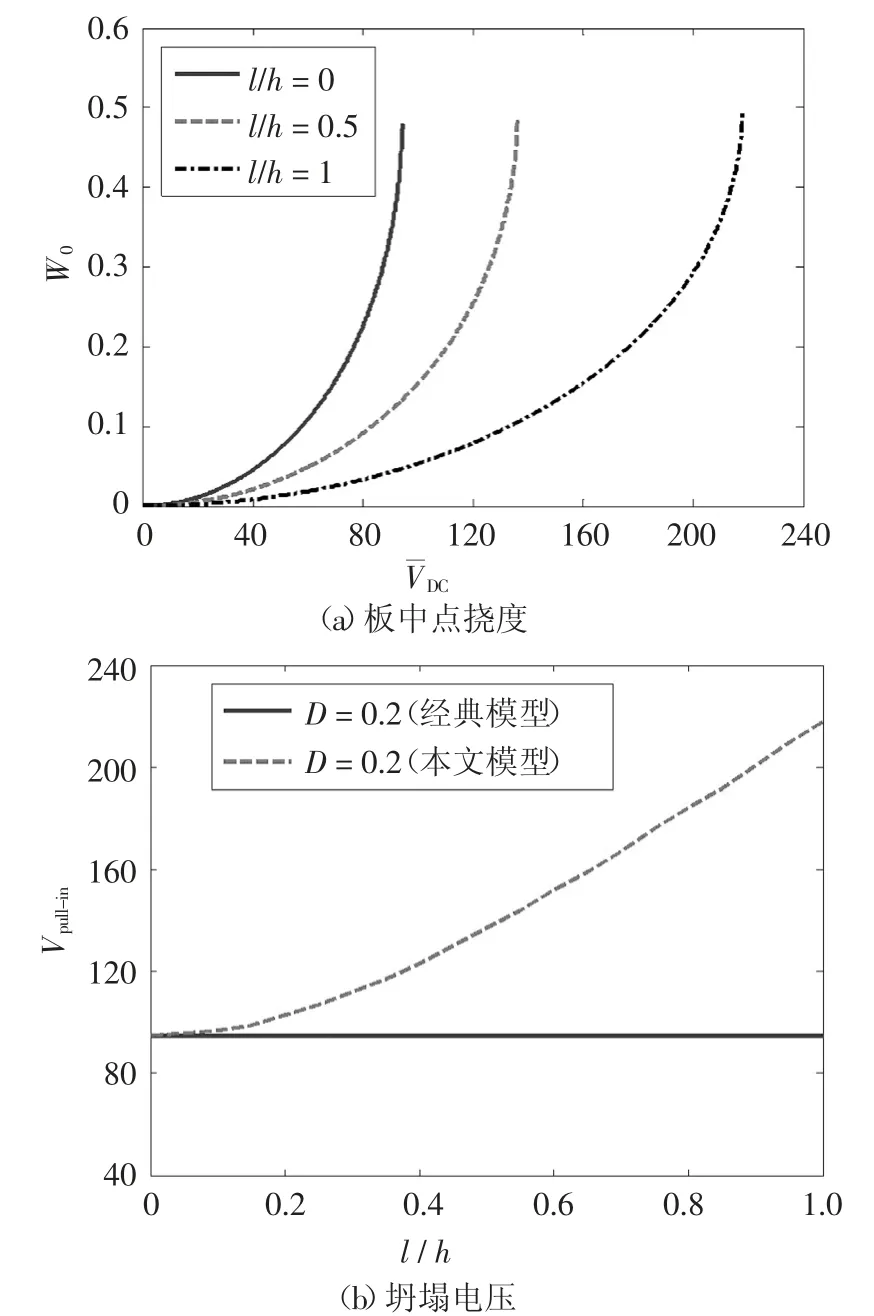
图4 尺度效应对板中点挠度和坍塌电压的影响Fig.4 Size effect on center deflection and pull-in voltage

图5给出了初始间距对板中点挠度和坍塌电压的影响.其中，图5（a）为不同初始间距对挠度电压曲线的影响（损伤变量和特征尺度参数分别为0.2和0.5）；图5（b）给出了本文模型（l/h=0.5）和经典模型（l/h=0）坍塌电压随初始间距变化曲线（损伤变量取0.2）.由图5可知，坍塌电压随着初始间距的增大而大幅增加.这是由于在电压不变的情况下电场力中的系数α与初始间距的立方d3呈反比.故初始间距增大会急剧减小电场力的大小.

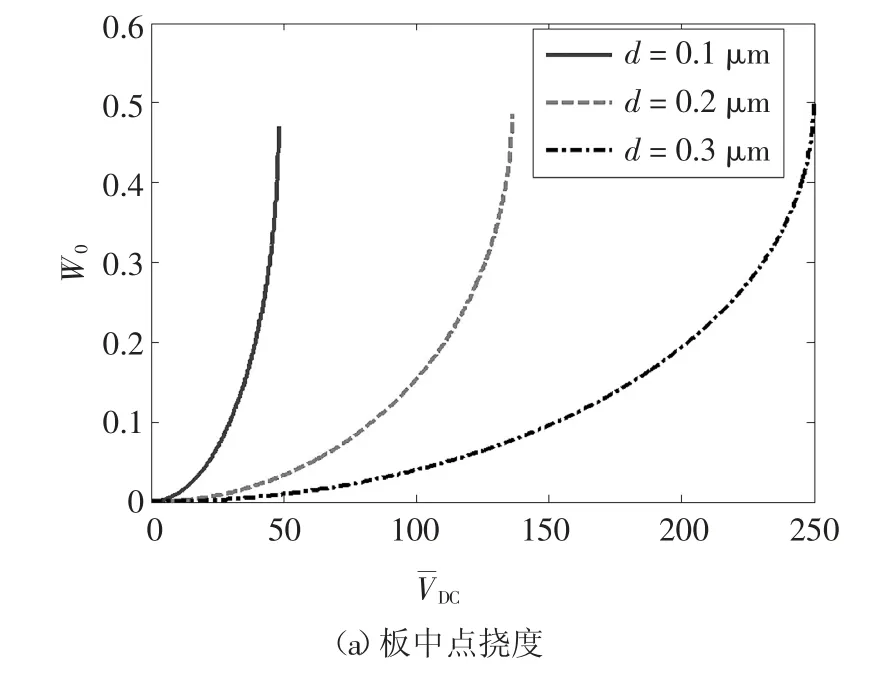
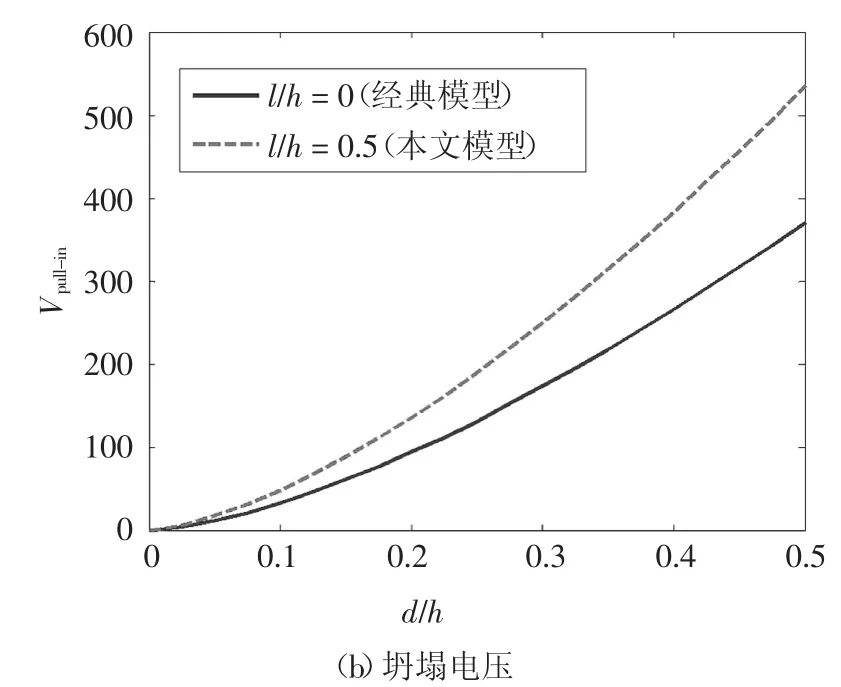
图5 初始间距对板中点挠度和坍塌电压的影响Fig.5 Influence of initial gap on center deflection and pull-in voltage

表2给出了边缘场效应对坍塌电压的影响.由表2可以看出，考虑边缘场效应时的坍塌电压比不考虑边缘场效应时的坍塌电压略小.从电场力的表达式（式（20））可知，边缘场效应会提供微结构额外的电场力作用，因此考虑边缘场效应时的坍塌电压会略微减小.

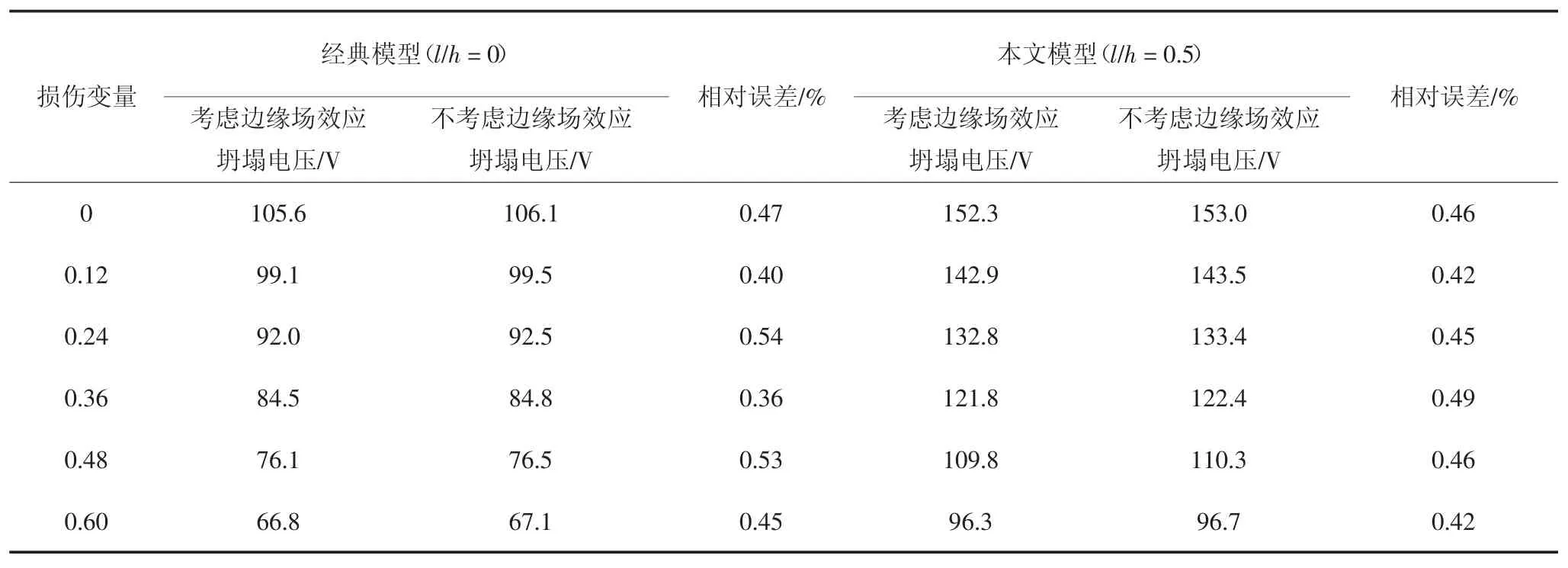
表2 边缘场效应对坍塌电压的影响Tab.2 Fringing effect on pull-in voltage

3 结论

本文通过数值计算对夹支微板在电场力作用下坍塌特性进行分析，并将所得结果与文献结果进行了对比，验证了本文模型的合理性，讨论了损伤效应、尺度效应、边缘场效应以及初始间距对微板坍塌电压的影响.研究结果表明，损伤效应会减小坍塌电压，而尺度效应会增大坍塌电压，坍塌电压会随着初始间距的增大而大幅增加，考虑边缘效应时坍塌电压会稍微减小但变化不大.本文所得结果对电致驱动微板结构设计具有一定的指导意义.