齿条类刀具展成加工修形齿廓的理论设计

冯锦平 周国鹏 蓝公仆

（1 湖北科技学院 工程技术研究院， 湖北 咸宁 437100）

（2 湖北香城智能机电研究院有限公司， 湖北 咸宁 437100）

（3 佛山科学技术学院 物理与光电工程学院＆粤港澳智能微纳光电技术联合实验室， 广东 佛山 528000）

（4 广东唯仁医疗科技有限公司 广东省“珠江人才计划”引进创新创业团队， 广东 佛山 528000）

0 引言

基节误差是引起齿轮啮入啮出冲击的重要因素，易导致齿顶刮行和接触应力大幅增加，恶化齿轮传动系统的振动噪声和缩短齿轮寿命。通过齿廓修形可以有效地改善上述问题，并提高齿轮传动的精度和平稳性[1-3]。

目前，针对齿廓修形的研究多侧重于修形参数的设计与优化，如采用B 样条曲线修形[4]，高阶曲线修形[5]，以承载传动误差、齿面闪温为目标优化多工况下齿轮的修形参数[6-7]等。随着数控技术的发展，业界逐渐开展了修形齿轮数控加工方法的研究，比如通过优化设计CNC 磨齿或者铣齿机床的多轴运动参数，加工齿轮拓扑齿形[8-10]，但是，对采用齿条类刀具加工修形齿廓的研究还很少。齿条类刀具（如滚刀）被大量地应用于齿轮加工。通常采用修形刀具加工修形齿廓，但是，修形刀具的加工适应性差，特定参数的刀具只能加工相应的修形齿廓，造成了修形刀具繁多，利用率低下等问题。随着数控技术的发展和刀具精度的提高，研究标准齿条类刀具展成加工修形齿廓的理论，有利于提高标准齿条类刀具的加工能力，避免对齿条类刀具进行修形加工，从而降低刀具成本。冯显英等[11-12]以标准渐开线齿轮滚刀为例，提出了正交联动变位创成修形齿廓的方法，通过增大刀具与工件的径向距离，同时控制刀具沿其轴向的位移，采用求解刀具包络线的方法，模拟了修形齿廓的加工效果。李左章等[13]在加工完渐开线齿廓后，基于正交联动变位位置模拟了数控滚刀加工修形齿廓的效果，并将该方法移植到华中I型数控系统以及YK5612数控插齿机中。以上研究采用求解包络线的方法，侧重考虑修形齿廓的包络创成过程，从理论和实践的角度证实了采用齿条类刀具数控加工修形齿廓的可行性，但没有定量对比模拟加工的修形齿廓与设计修形齿廓的一致性，没有考虑修形齿廓的啮合点偏离渐开线齿廓啮合线后对刀具加工位置的影响，也未说明刀具与齿轮在加工1个修形齿廓转角周期内的相对运动关系。

本文中围绕齿条类刀具加工修形齿廓的全时刻速度控制方程和精确地加工复现出修形齿廓这两个核心问题，不考虑齿轮加工过程中的热变形、承载变形及制造加工误差对加工修形齿廓的影响，提出了采用分段的传动误差模型描述齿条类刀具在全时刻的速度控制方程的方法；采用轮齿接触理论，精确地计算出修形齿廓与齿条类刀具在啮合线外啮合的传动误差，确保在理想情况下齿条类刀具展成修形齿廓理论上的完整性和准确性。以齿条类刀具加工直齿轮修形齿廓为例，加工工序为：先完成渐开线齿廓加工；再基于正交联动变位理论，将刀具移动到修形加工位置；最后，依据传动误差模型控制齿条类刀具（如滚刀）的旋转速度，完成修形齿廓的加工。根据加工1个修形齿廓周期内刀具与齿轮工件的啮合状态，将整体传动误差曲线分解为3段，分别为加工修形齿廓的修形加工段、与渐开线齿廓啮合的渐开线啮合段和未与轮齿接触的空啮合过渡段。在设计修形加工段传动误差模型时，充分考虑了齿条类刀具与修形齿廓的展成点偏离标准渐开线齿廓啮合线对传动误差的影响，确保了模拟展成的修形齿廓与理想设计修形齿廓一致，完善了采用齿条类刀具展成加工修形齿廓的理论。

1 齿条刀具与齿轮的传动误差设计

标准齿条刀具在图1所示标准位置加工渐开线齿轮时，由于重合度大于1，齿条刀具与齿轮在齿顶I处和齿根II 处同时啮合，若对齿轮进行修形加工，会破坏相邻轮齿根部齿廓的形状，所以，标准齿条刀具在标准位置不能加工修形齿廓。通过增大齿条刀具和齿轮的径向距离至图1中的修形位置，可减小重合度。当重合度小于1时，齿条刀具与齿轮只存在1个啮合点，可以实现对齿顶齿廓的修形加工，同时避免了与相邻齿的互相干涉。完整的修形加工工序为：先加工标准渐开线齿轮；再将齿条刀具移位到修形位置，加工齿顶修形齿廓。为了保证加工过程具有可延续性，修形位置齿条刀具与标准位置齿条刀具的加工轮廓保持共线。因此，修形位置与标准位置的刀具与渐开线齿轮具有统一的啮合位置关系。

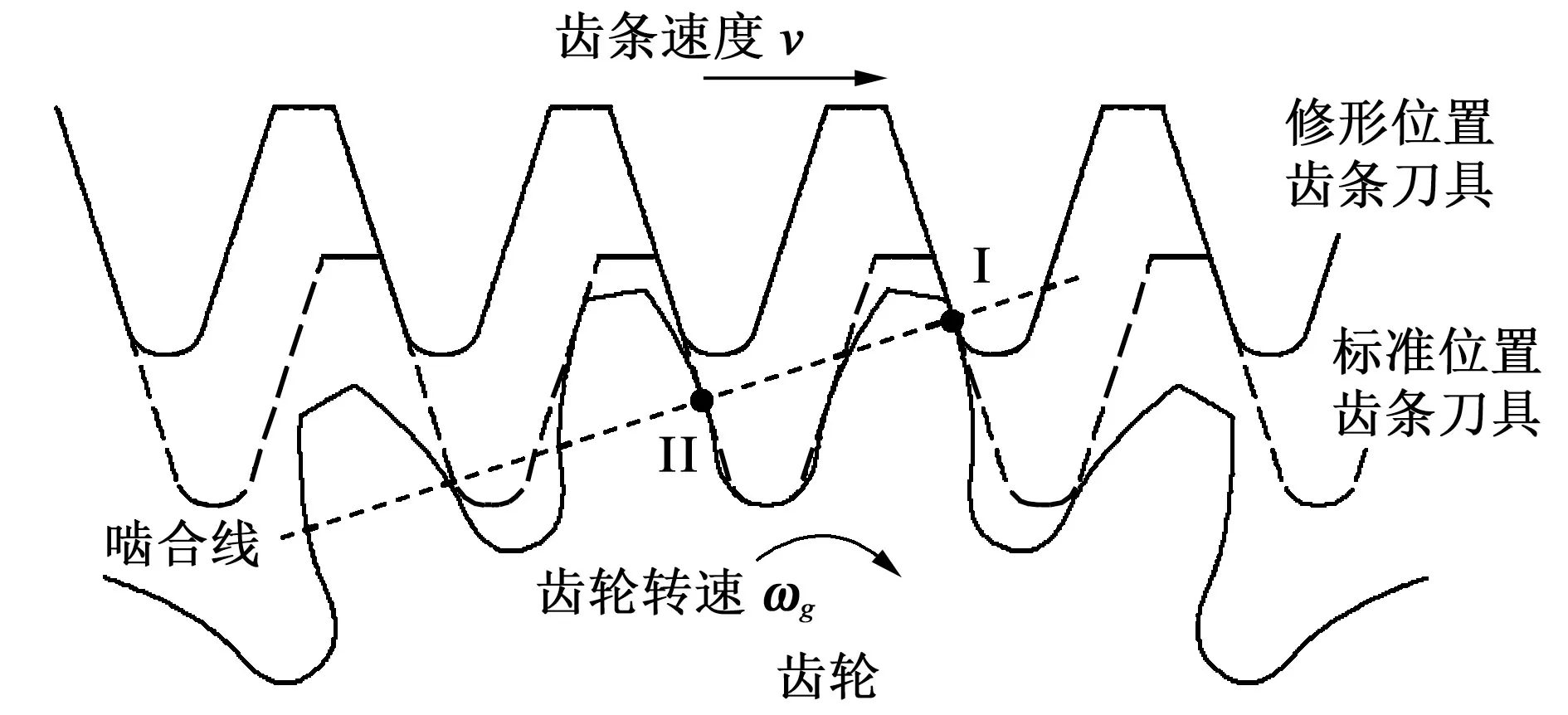
图1 齿条刀具与齿轮啮合位置Fig.1 Meshing positions of rack cutters and gears

根据轮齿啮合分析理论，已知修形齿廓参数、刀具齿廓参数，可以确定刀具与修形齿轮的相对运动关系即传动误差。反之，若齿条刀具按照设计的传动误差加工齿轮，可加工对应的修形齿廓。所以，为了加工齿顶修形齿廓，设计了如图2所示的传动误差曲线。图2 中，M3M4为修形加工段，对应齿轮修形段齿廓与齿条刀具的传动误差，基于齿廓理论修形方程及轮齿接触分析理论计算；M2M3为渐开线啮合段，传动误差为0，对应齿轮的一部分渐开线齿廓与齿条刀具啮合；M1M2为空啮合过渡段，齿轮与齿条刀具在该段啮合时未产生实际接触，其主要作用是实现齿条刀具与轮齿平滑的进入和退出啮合，并保证刀具速度平滑。以图1中加工齿轮右侧齿顶修形齿廓为例，M1、M4分别为对应齿顶退出啮合位置；M2为对应齿条刀具与渐开线齿廓切入啮合位置；M3为对应齿廓修形起始位置。

图2 齿条刀具与齿轮啮合的传动误差曲线Fig.2 Transmission error curve of gear meshing with rack cutters

传动误差的设计流程如图3所示。设计的关键在于根据齿廓理论修形方程精确推导计算修形齿轮的啮合转角和对应的传动误差。

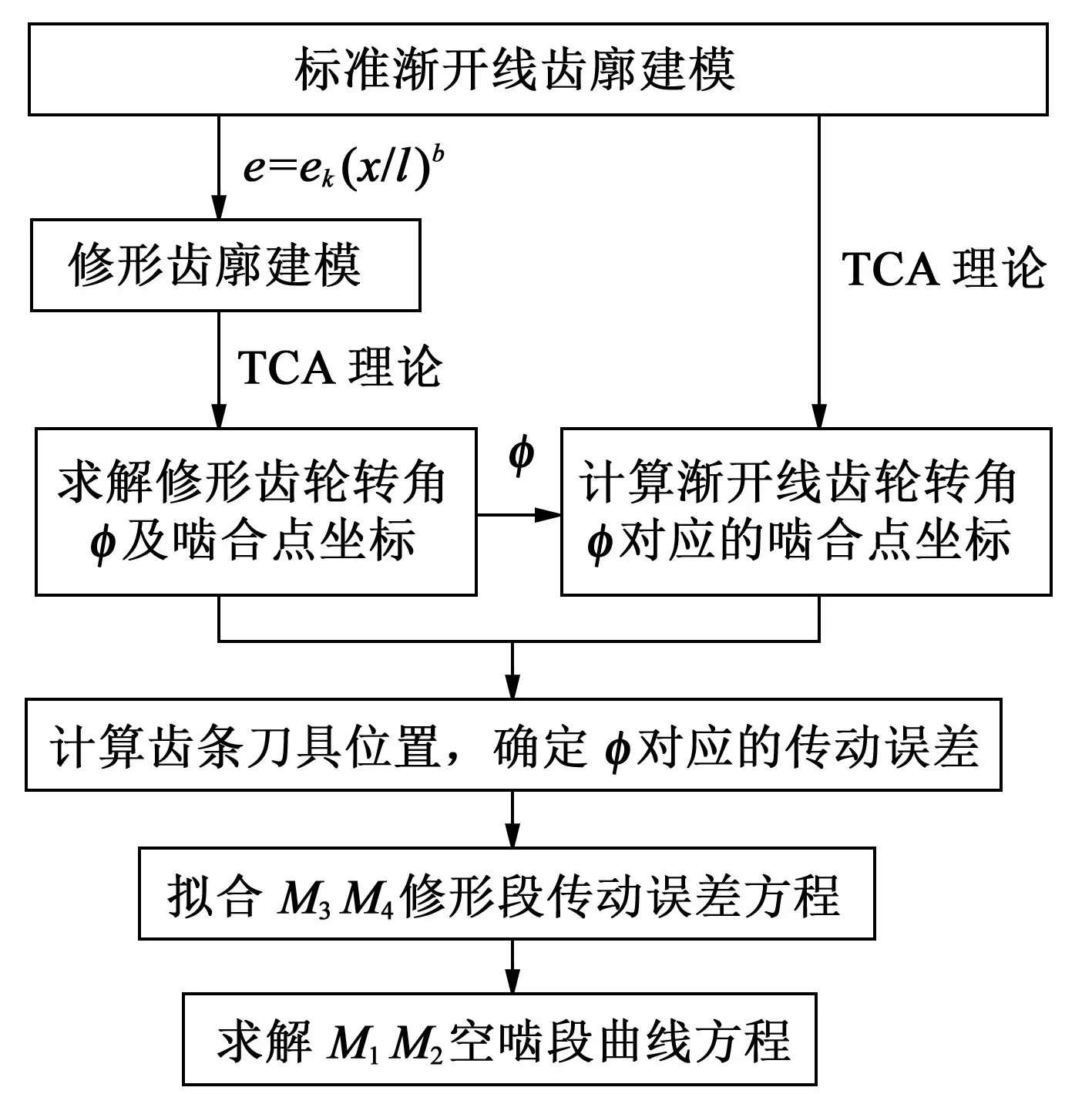
图3 齿轮齿条刀具啮合传动误差模型设计流程Fig.3 Transmission error model design process of gears and rack cutters

齿轮齿条刀具传动误差的设计过程如下所述。

1.1 标准渐开线齿廓建模

首先，建立齿条刀具的轮廓方程；然后，按照理论传动关系，依据轮齿接触理论，采用坐标变换矩阵方法，建立标准渐开线齿廓模型。

图4（a）所示为齿条刀具的模型。记rt为齿条坐标系otxtyt下刀具直线段AC的齐次向量，有

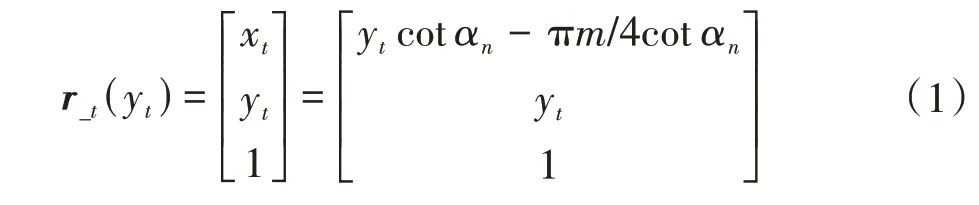
式中，yt≥πm/4 -BCsinαn，

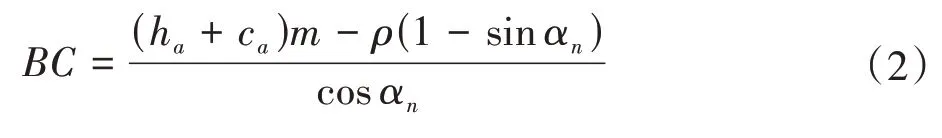
其中，ha为齿顶高系数；ca为顶隙系数；m为模数；αn为压力角；ρ为刀具CD段的圆弧半径。

图4（b）所示为齿轮与齿条刀具啮合时的坐标关系。以S1表示渐开线齿轮的局部坐标系o1x1y1，随齿轮转动而转动；以St表示齿条坐标系otxtyt；以Sa1表示辅助坐标系oa1xa1ya1，其坐标轴保持固定；M为啮合点；xi为变位系数；rp为分度圆半径；θ为渐开线齿轮与齿条啮合时的理论转角。根据齐次坐标变换方法可得

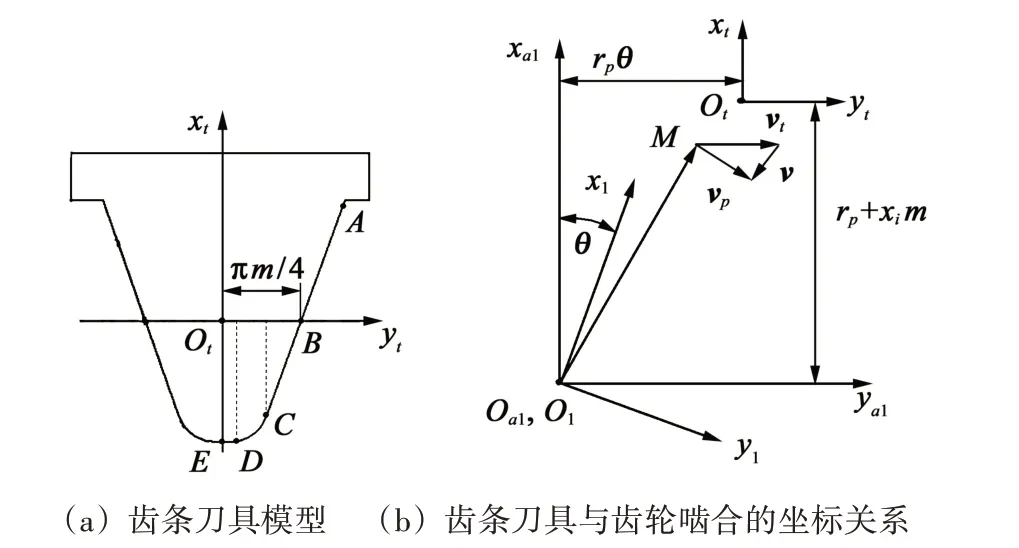
图4 齿条刀具模型及加工啮合坐标关系Fig.4 Rack cutter model and coordinate relation of machining meshing

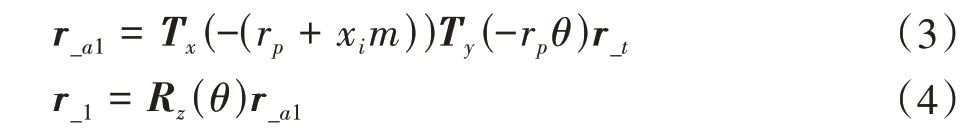
式中，r_a1、r_1分别为齿条刀具轮廓在辅助坐标系Sa1、齿轮局部坐标系S1下的齐次向量；Rz（θ）、Tx（L）、Ty（L）均为坐标转换矩阵，表达式分别为

齿条刀具与齿轮在M点啮合，满足啮合方程，啮合点处的齿廓法向向量和相对速度向量的点积为0，即

式中，n为啮合点M的齿廓法向量；v为齿条刀具与齿轮在啮合点处的相对速度。根据式（8），可将θ表达为rt中变量yt的函数。给定式（3）、式（4）中yt的取值，则可确定对应的啮合点坐标，得到渐开线齿廓。

1.2 修形齿廓建模

齿廓理论修形方程通常沿啮合线表示为

式中，ek为最大修形量，本文中取负值；x为修形点相对界点的距离；l为最大修形点与界点的距离；x、l均沿啮合线度量，界点是修形起始点；幂指数b一般取1.0～2.0。齿廓修形方程在啮合线上的度量方法如图5所示。

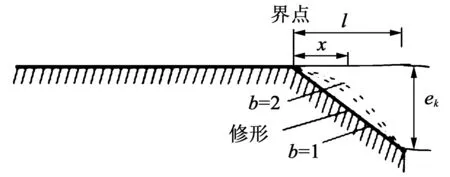
图5 齿廓修形方程在啮合线上的度量Fig.5 Measurement of tooth profile modification equation along the meshing line

将渐开线齿廓沿啮合线向轮齿内部偏移相应修形量可获得修形齿廓。在辅助坐标系Sa1下，标准渐开线齿轮与齿条刀具的啮合线通过节点，则通过在Sa1坐标系中将渐开线齿廓沿啮合线偏移相应修形量，得到在图1修形位置加工的修形齿廓表达式为

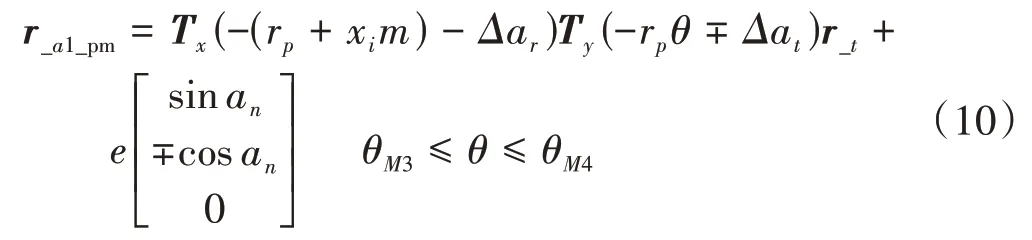
式中，Δar为齿条刀具修形位置相对标准位置沿xa1方向的距离；Δat为沿ya1方向的距离，均采用第2节中提供的设计方法确定。当齿轮按图1所示运行方向加工右侧修形齿廓时，上式取“+”号；加工左侧修形齿廓时，上式取“-”号。θM3和θM4分别为渐开线齿轮在修形起始点和终止点与刀具啮合时的转角，由式（8）求解。

通过旋转Sa1坐标系角度θ与S1重合，得到在S1坐标系下的修形齿廓为

1.3 修形加工段的传动误差计算

第1.1 节中定义了理论转角θ，表示标准渐开线齿廓与齿条刀具啮合时齿轮的转角；在此引入实际转角ϕ，表示修形齿廓与齿条刀具啮合时的齿轮转角。加工修形齿廓时，啮合点位于啮合线外，需要采用数值方法求解修形啮合点的坐标，再与处于相同转角位置的标准渐开线齿轮的啮合点坐标对比，获取修形齿廓与齿条刀具的传动误差。在加工修形齿廓过程中，实际转角ϕ与理论转角θ是两个独立的变量。修形齿廓在坐标系Sa1中的表达式为

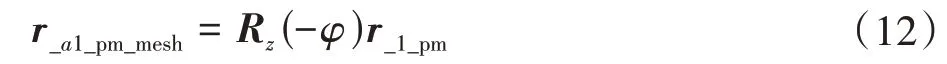
根据刀具与修形齿廓在啮合点处切线的斜率相等，可得

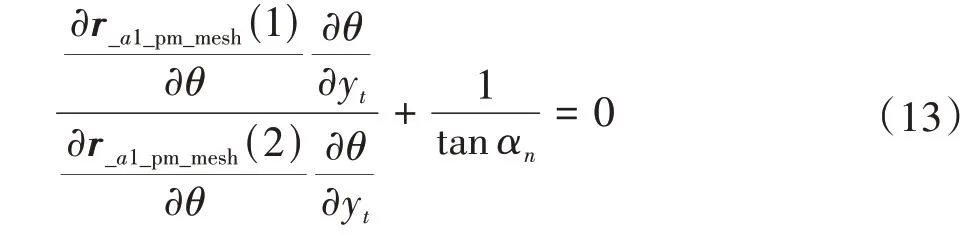
式中，r_a1_pm_mesh（1）为啮合点在Sa1坐标系中的x坐标值；r_a1_pm_mesh（2）为y坐标值；αn为齿轮压力角。

由式（8）中可知，理论转角θ是yt的函数，在给定齿条刀具yt的情况下，由式（13）求解实际转角ϕ，代入式（12），可计算得到修形齿轮转角为ϕ时的啮合点坐标值。

为了计算传动误差，还需要求解渐开线齿轮转角θ等于ϕ时的啮合点坐标值。由式（3）和式（8），获得标准渐开线齿轮的啮合点坐标为

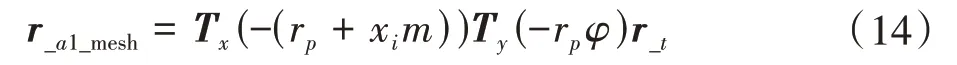
已知齿条刀具轮廓斜率及加工修形齿廓和渐开线齿廓的啮合点坐标，可计算刀具沿yt方向的平移量即传动误差。

齿条刀具齿廓延长线与ya1轴的交点y值为

式中，by_pm为加工修形齿廓对应的y轴截距；by_inv为加工渐开线齿廓对应的y轴截距；加工右侧修形齿廓时取“+”号，加工左侧修形齿廓时取“-”号。

齿轮齿条刀具的传动误差为

1.4 修形加工段传动误差拟合建模

求解出位于各转角的修形齿轮与齿条刀具的传动误差后，拟合修形加工段传动误差Te_pm与齿轮实际转角ϕ的表达式。修形起始点对应的转角按式（13）求解，记为ϕM3，建立传动误差曲线M3M4段的三次项拟合方程为

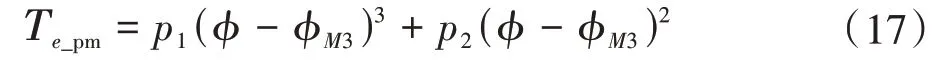
式中，p1、p2均为待求的拟合系数；ϕM3≤ϕ≤ϕM4，其中，ϕM4根据修形齿廓点的向量模与齿顶圆半径相等求解。

1.5 一齿转角周期的传动误差模型

M3M4为修形加工段，传动误差按式（17）求解。

M2M3为渐开线啮合段，传动误差为0，即

式中，ϕM2≤ϕ≤ϕM3；ϕM2=ϕM3-ϕM2M3。

M2M3是空啮合过渡段与修形加工段传动误差的衔接线，不可为负值，最小值可取0。可以自行给定合理的小转角ϕM2M3。

M1M2为空啮合过渡段，其方程为

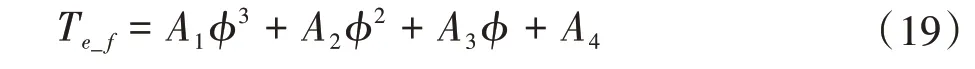
式中，ϕM1≤ϕ1≤ϕM2；ϕM1=ϕM4- 2π/zg。

根据刀具运动的连续性条件，即传动误差曲线在M1点、M2点的位置坐标及其斜率（由式（17）、式（18）求导）相等，可以列出4个等式，唯一确定A1、A2、A3、A4。

2 刀具与齿轮的径向及切向位置设计

在修形位置，齿条刀具的直线段齿廓顶点与图6所示齿轮啮合线的D0点啮合。其中，D0E0线段的距离为lc，计算式为

根据图6中的几何关系，可以确定修形位置齿条刀具的分度线与齿轮中心的径向距ar为

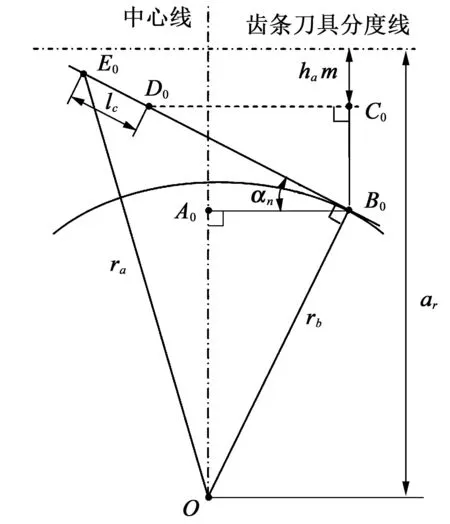
图6 修形位置齿条刀具分度线与齿轮中心的径向距离Fig.6 Radial distance between the rack cutter dividing line and the gear center at the modification position

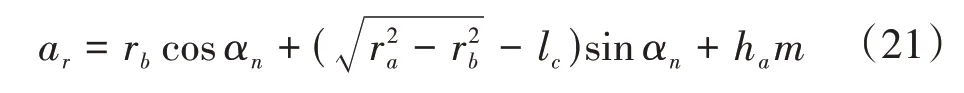
式中，ra为齿顶圆半径；rb为基圆半径。

则齿条刀具的修形位置比标准位置沿齿轮的径向（xa1坐标）远离齿轮的距离Δar为

齿条刀具再沿齿轮切向移动，使刀具齿廓在修形位置和标准位置共线，则齿条刀具的修形位置相对标准位置沿齿轮切向（ya1坐标）移动距离Δat为

式中，加工图1 所示齿轮右齿廓时取“+”号；加工左齿廓时取“-”号。

3 刀具与齿轮的速比关系

实际加工时，齿条类刀具可以是滚刀或者其他。将齿条类刀具与齿轮的位置关系转换成速度关系，设齿轮转速恒为ωg，刀具齿廓的位移s（t）等于等效齿条刀具的展成位移，则

将式（17）～式（19）中的实际转角ϕ以ωgt代替，根据传递误差的周期性，可得传动误差Te（t）。

已知s（t），以滚刀刀具为例，齿轮工件匀速转动时，刀具的转动速度方程ωt（t）为

式中，zt为滚刀头数。

按照以上的加工位置关系和速度方程，可以数控加工齿顶修形齿廓。

4 修形示例

以直齿轮为例，设模数为6 mm，齿数为20，压力角为20°，变位系数为0，齿顶高系数为1，最大修形量为15.0 μm。则沿啮合线度量的理论修形方程为

以单头滚刀加工齿轮右侧修形齿廓为例，求解出修形齿轮转角与相应的传动误差后，根据式（17）拟合得到修形加工段的传动误差方程为

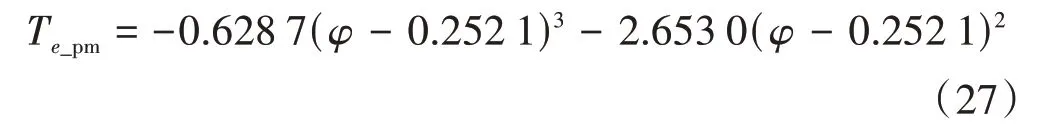
拟合效果如图7 所示。R2系数为1，标准差为4.3×10-7mm。

图7 齿轮修形加工段传动误差Fig.7 Transmission error of gear modification section

求解空啮合过渡段的传动误差方程为

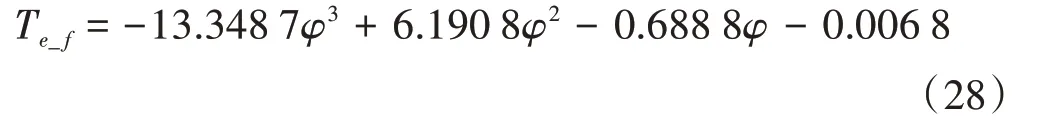
图8所示为计算得到的齿条刀具与齿轮的周期性传动误差。本例中，齿条刀具的最大传动误差为18.5 μm，相当于齿条刀具沿其齿廓法向即啮合线方向移动了17.4 μm，比沿啮合线度量的最大修形量15.0 μm 大了许多，这是由于修形齿廓在由理论转角θ计算的修形点处与齿条刀具啮合时，修形齿轮的实际转角ϕ大于理论转角θ所致。

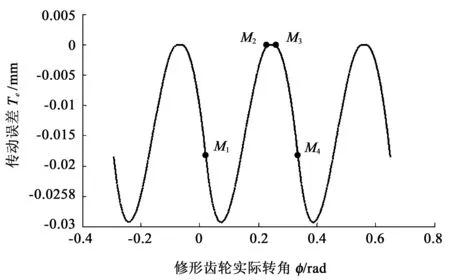
图8 加工修形齿廓的周期性传动误差Fig.8 Periodic transmission error in machining modified tooth profile

下面通过对比基于传动误差模型模拟加工的修形齿廓曲线、刀具相对轮齿的加工运动轨迹的包络线轮廓以及根据齿廓修形方程建立的修形齿廓曲线偏差，验证本文中提出的方法在理论上的正确性。

图9所示为计入传动误差的影响，获取的处于修形位置的齿条刀具相对轮齿的加工运动轨迹。齿条刀具的运动轨迹包络线即为加工切削轨迹。由图9中可知，刀具在加工修形齿廓时与其他轮齿未产生干涉。

图9 齿条刀具在加工修形齿廓时相对齿轮的运动轨迹Fig.9 Motion trajectory of rack cutters ralative to gears when machining the modified tooth profile

图10（a）所示为基于传动误差模型模拟加工的修形轮廓与刀具运动轨迹包络线轮廓的对比，两者整体重合。图10（b）所示为局部放大的齿廓修形部分，可以看出，模拟加工的修形齿廓与刀具运动轨迹的包络线一致。

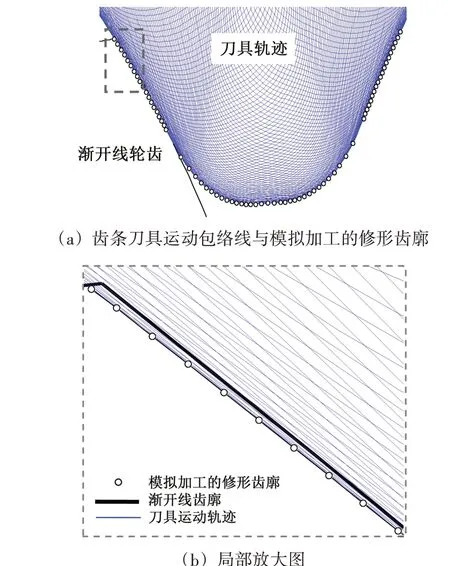
图10 齿条刀具运动包络线与模拟加工的修形齿廓对比Fig.10 Comparison between rack cutter motion envelope and simulated modified tooth profile

图11 所示为模拟加工的修形齿廓与理想设计的修形齿廓的对比，可以看出，两者一致。模拟加工的修形齿廓点偏离理想设计的修形齿廓距离的最大值为1.33×10-14mm，平均值为2.81×10-15mm。因此，可以认为模拟加工的修形齿廓与理想设计的修形齿廓完美重合。

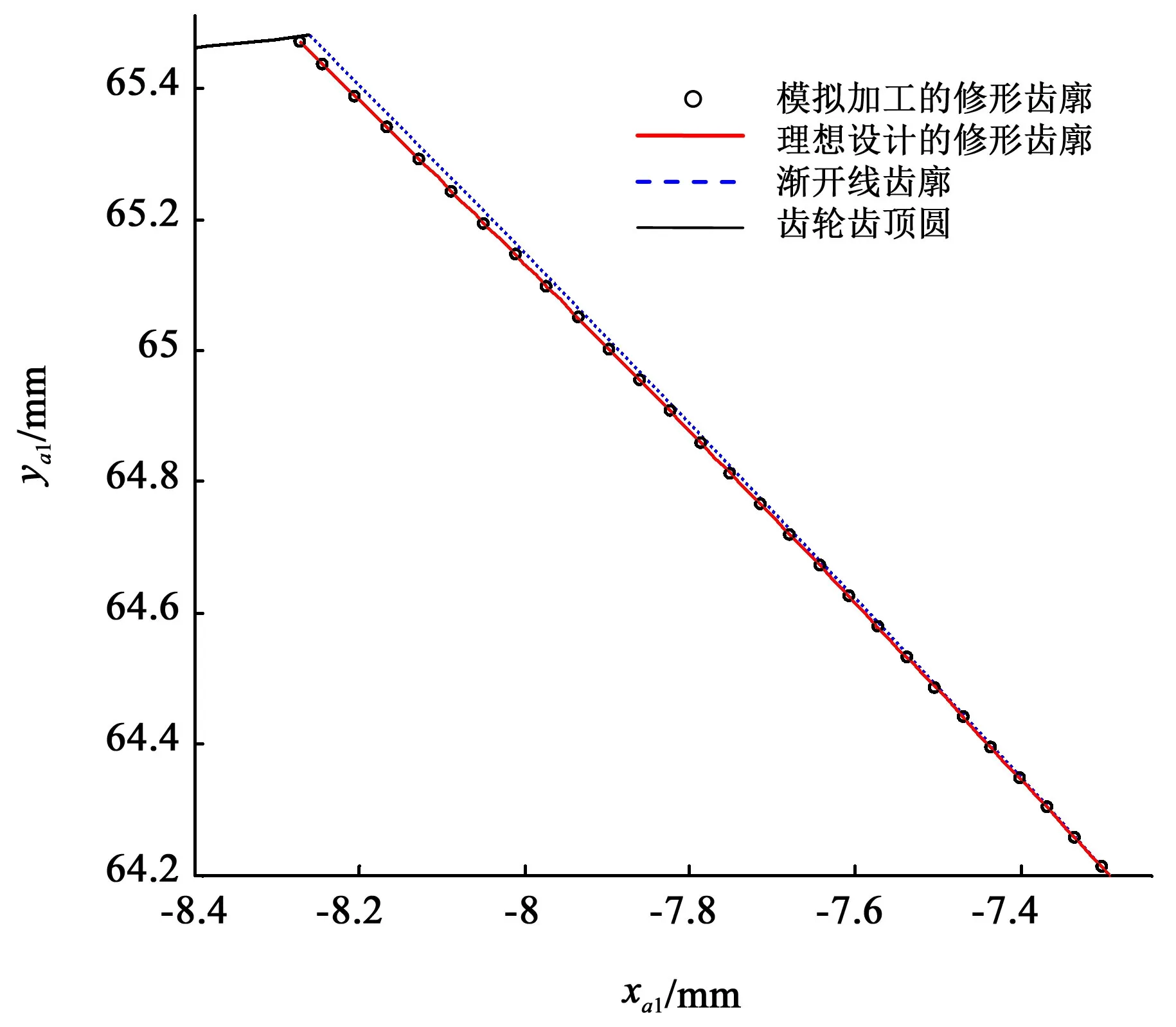
图11 理论修形齿廓与模拟加工修形齿廓的对比Fig.11 Comparison between theoretical modified profile and simulated modified profile

通过对比模拟加工的修形齿廓、刀具的运动轨迹包络线轮廓以及理想设计的修形齿廓可知，3条齿廓曲线重合，说明了齿条类刀具基于传动误差模型展成加工齿廓修形方法的正确性。

5 结论

根据沿啮合线度量的理论齿廓修形方程，采用轮齿接触分析理论推导出齿条类刀具在修形位置加工修形齿廓的传动误差模型及刀具的速度控制模型。在不考虑热变形、承载变形以及加工制造误差的情况下，基于传动误差模型模拟加工的修形齿廓与理论设计的修形齿廓重合。

（1）设计了加工1个修形齿廓周期内的完整传动误差曲线，重点设计了修形加工段传动误差模型和空啮合过渡段传动误差模型。完整的传动误差模型为齿条类刀具在任意时刻的速度提供了具体的方程，能为数控加工控制提供依据。

（2）齿条类刀具与修形齿廓啮合的传动误差不能定量为齿条类刀具齿廓从渐开线啮合点沿啮合线偏移到修形齿廓点的距离，需要精确计算出修形齿廓与齿条类刀具在啮合线外的啮合点的准确坐标，才能保证加工出来的修形齿廓与理论设计修形齿廓重合。

（3）空啮合过渡段传动误差模型保证齿条类刀具展成加工修形齿廓时，其位移及速度具有连续性，且能与工件齿轮平滑地进入及退出啮合。

本文中提出的齿条类刀具展成修形齿廓理论可用于指导齿廓修形加工。其不仅适用于标准的齿条刀具，也能扩展到具有不同齿廓方程的齿条类刀具；不仅适用于传统的幂次修形方程，也适用于其他修形方程，具有通用性。但该方法对齿轮机床（如数控滚齿机）的性能也提出了更高的要求，要求在加工修形齿廓时需要解除齿轮工件与滚刀的固定速比关系，增加速度控制环，提高控制系统带宽以及提升刀架系统和机床的动态响应特性。