基于机器视觉的齿廓偏差测量方法
2021-04-13曹鹏勇王建文程敏杰
曹鹏勇, 王建文, 程敏杰
(华东理工大学机械与动力工程学院, 上海 200237)
齿轮是实现机械传动的重要零部件之一,而齿轮的齿廓偏差是判断齿轮运动平稳性的直接因素。故针对如何提高产品齿轮的检测和加工制造精度的研究具有非常重要的意义[1]。传统的齿轮偏差测量方法为接触式测量,该方法测量效率低,价格成本高,存在主观误差且会对齿轮齿面造成一定损伤。如文献[2]采用三坐标测量仪来获取齿廓坐标,并进行齿廓拟合求出齿廓偏差,操作复杂、效率低且成本高。
现提出一种新的齿廓偏差的非接触测量方法:通过机器视觉的手段采集齿轮图像,采用Zernike矩亚像素边缘检测算法[3]获得清晰的亚像素级齿轮边缘,并分割、采集齿轮的齿廓数据获得参考点云。结合反求工程的思想,以实测齿轮的各项设计参数为基础并依据渐开线的形成原理来构建齿轮的理论模型[4],获得齿轮的参考点云数据,建立齿轮的反求数字化模型[5]。将获得齿轮的目标点云和参考点云数据后,通过二维迭代最近点(iterative closest point, ICP)算法[6]进行点云数据配准,最终获得齿轮的齿廓偏差,最后通过齿廓目标点云和参考点云偏差对比计算,验证所提齿轮齿廓测量方法的正确性。
1 参考点云数据采集
标准齿轮数字模型是以待测齿轮为基础构建的齿轮模型。模型构建的目的是与后续机器视觉获得的点云数据进行对比和配准,进而获得齿轮的齿廓偏差,依此来评价上述测量方法的可行性和准确性。选择精度等级为8的中低速度汽轮机用齿轮为研究对象,在MATLAB环境下,根据齿轮测绘的基本参数(表1)和渐开线直齿轮的形成原理,结合如图1所示三维齿轮,利用图形学的方法建立标准直齿轮数字模型。

图1 标准齿轮的三维模型Fig.1 3D model of standard gear

表1 齿轮基本参数Table 1 Basic parameters of gear
根据齿轮三维模型构建标准齿轮数字模型,剔除齿顶圆、基圆和分度圆数据,只留下齿廓部分。在MATLAB开发环境下建立齿轮齿廓图,如图2所示。为采集齿廓参考点云,根据左右齿廓的数据特征创建变量存储齿廓的坐标,并将数据转换为asc格式方便后续处理,即为齿廓的参考点云数据。
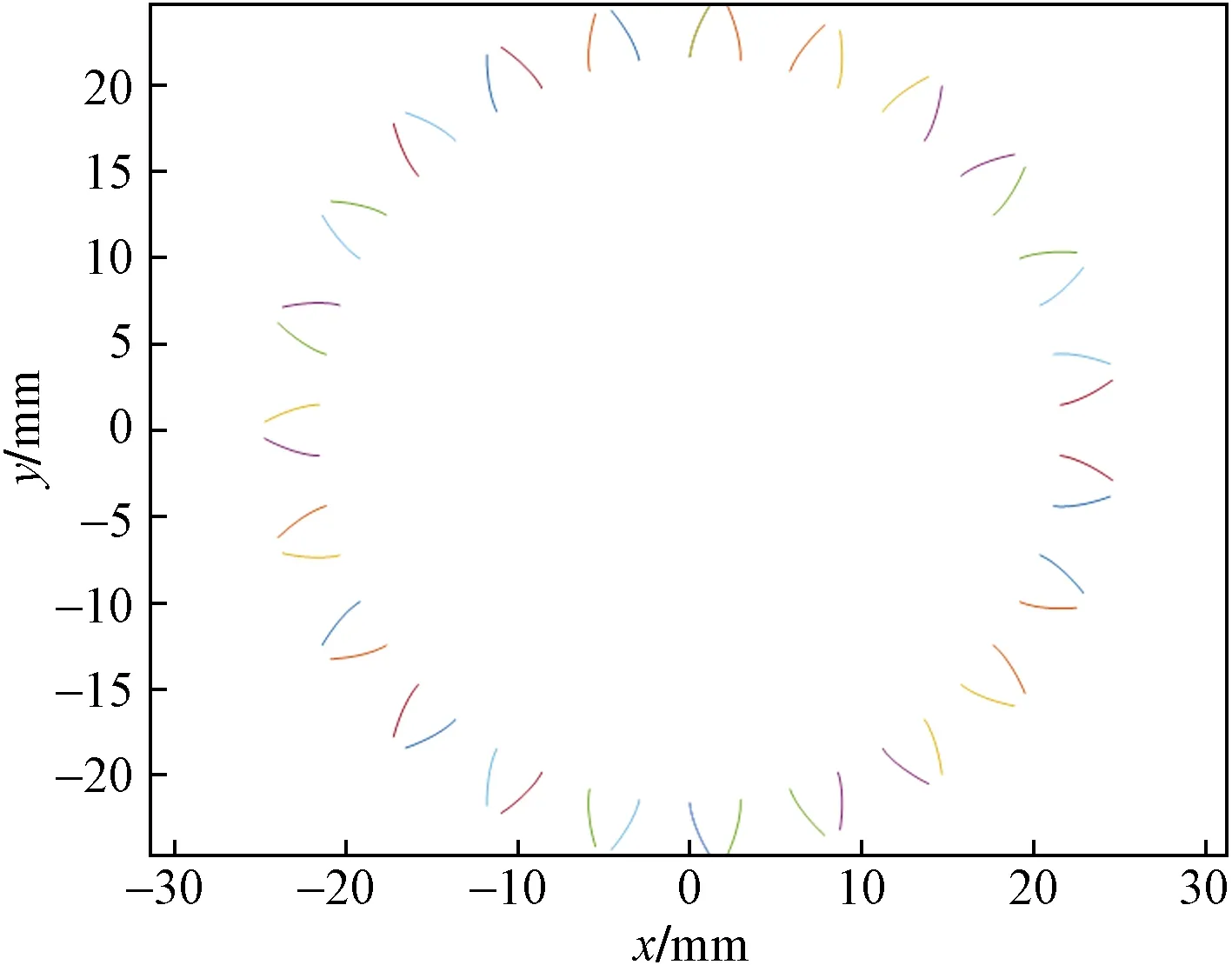
图2 标准齿轮数字模型的齿廓Fig.2 Tooth profile of the standard gear digital model
2 目标点云数据采集
运用机器视觉的方法采集目标点云:首先利用工业相机采集齿轮图像,经由MATLAB软件对采集到的图像进行灰度化、高斯滤波、二值化等处理,达到提高图像质量、改善清晰度的目的。再对处理后的图像进行边缘检测,文献[7]研究了经典的边缘检测算法,获得的边缘较粗。图像处理结合齿轮的图像特征采用Zernike矩亚像素边缘检测算法[8],以(x,y)为圆心坐标,设灰度图像函数为f(x,y),则Zernike矩表达式可写为
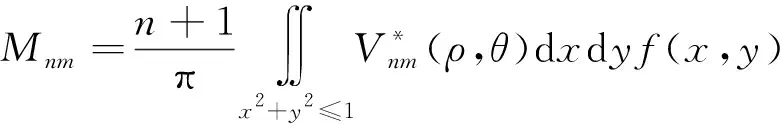
(1)
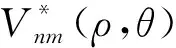

(2)
式(2)中:M11为Zernike矩。令Zernike矩的模板阶数为N,对于已知边缘点坐标为(m1,n1),则相应的亚像素坐标为(mz1,nz1),有
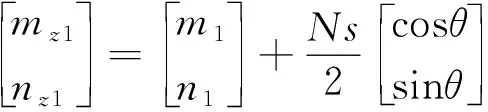
(3)
式(3)中:N为Zernike矩的模板阶数。
通过亚像素坐标计算并进行形态学滤波最终可获得清晰的齿轮边缘,如图3所示。

图3 齿轮齿廓边缘Fig.3 Edge of thegear tooth profile
为减少运算量,提高配准精度,将所获齿廓,去除齿顶圆、齿根圆数据只留下齿廓数据。采用连通区域法获取齿轮的外接矩形,用于去除冗余数据,其中:矩形中心即为齿轮中心。计算齿廓边缘到齿轮中心的距离,剔除距离大于等于齿顶圆、小于基圆的点,如图4所示。图4(a)所示曲线图为由齿轮边缘到齿轮中心的距离,通过提取齿廓的目标点云数据,并将点云数据存储在预先设定好的变量中,即完成齿廓的目标点云数据采集,配准结果如图4(b)所示。

图4 齿轮的目标点云采集图Fig.4 Acquisition of the gear target point cloud
3 基于简化齿廓的ICP算法点云配准

根据欧氏最小二乘法计算距离空间中两个点集之间的最佳对应关系,列协方差函数为
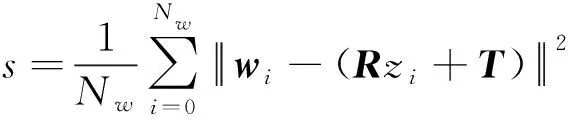
(4)
式(4)中:R为旋转矩阵;T为平移矢量矩阵;s为两点间最短距离。
利用ICP算法配准齿轮齿廓点云步骤如下:
(1)给定初始旋转矩阵R,平移矢量矩阵T,以及最大迭代次数k,计算得出齿廓目标点云W和参考点云Z。
(2)迭代配准确定对应度并通过最小化误差来计算两个图像点集之间的最佳变换Rk和Tk。
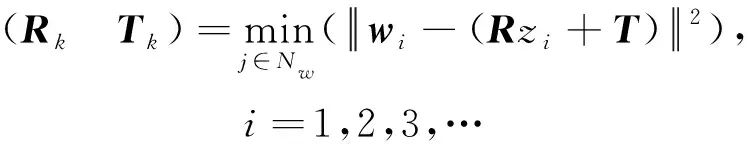
(5)
wk+1=Rkwk+Tk
(6)
(3)根据式(5)计算得矩阵R和T,确定目标点云wk按式(6)变换至wk+1,结合参考点云zk,计算出对应点对点间最短距离sk。
(4)不断迭代,直至收敛。对W中的每个点,在Z中寻找距离最近的点,不断迭代直到满足迭代条件:|sk-sk-1|<ε,其中ε为无穷小量,进而实现两点云之间相似度最大化。图5为同一坐标系下,点云W和点云Z中心重合后的点云图,图6为运用ICP算法配准结果,易看出基于ICP的点云配准方法利用最小二乘法寻优并不断迭代,适应性好且配准精度较高。

图5 中心对齐后的齿廓点云图Fig.5 Point cloud of tooth profile after center alignment
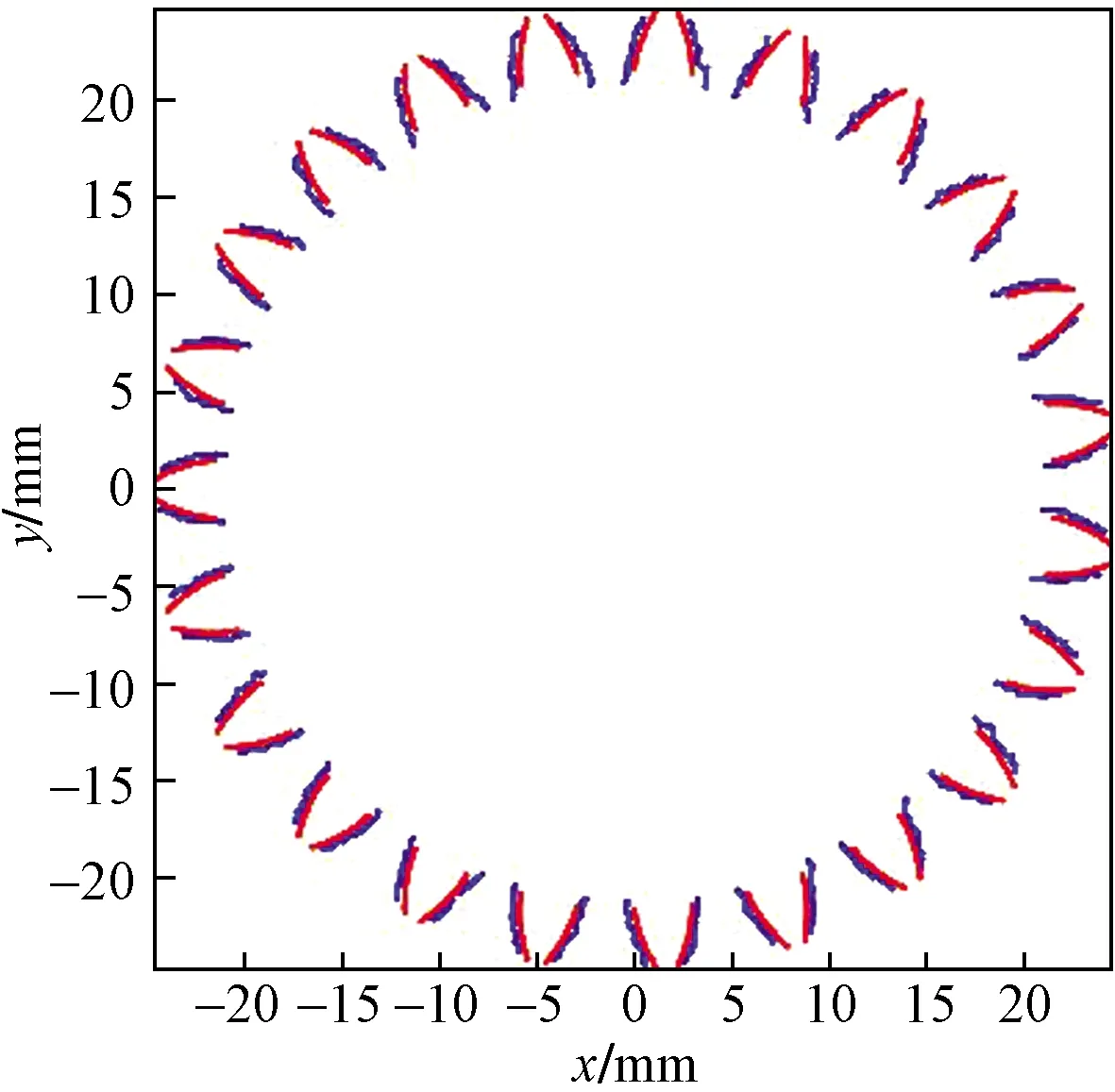
图6 齿廓点云的ICP配准结果Fig.6 ICP registration results of tooth profile point cloud
4 齿廓偏差的测量
齿廓偏差Δf是指在齿轮端截面上,齿形工作部分内(不含齿顶的倒棱部分),容纳实际齿形且距离最小的两条设计齿形之间的法向距离[12]。为测量齿轮的齿形误差,由其定义可知需获取包含实际齿廓的两条理论渐开线。如图7所示。
从点云配准结果图中选取一个齿廓并放大,效果如图8所示。其中局部参考点云共有14个,局部目标点云共有20个,单个齿廓配准结果图和图7齿廓偏差定义图是相似的,证明该方法具有可行性。

图7 齿廓偏差的示意图Fig.7 Schematic diagram of the tooth profile deviation

图8 单个齿廓数据放大图Fig.8 Enlarged diagram of individual tooth profile data
为测量齿廓偏差,采用多项式拟合离散目标点云得到如图9中线性拟合曲线,其基本原理为根据局部目标点云W中数据点(xi,yi),设拟合多项式为

图9 齿廓点云配准结果图Fig.9 Registration result of point cloud of tooth profile

(7)
式(7)中:Aj为待求未知数,令yi为第i个样本的真实值,当取样m个时,得到基于点云W真实值与预测值间偏差Q为

(8)

计算局部参考点云中的每个点到拟合曲线的距离,距离的平均值即为齿廓偏差。多项式拟合结果为
y=0.838x2+7.384x-7.843
(9)
计算局部参考点云中的每个点到拟合曲线的位移,取点位移曲线上方为正,测量偏差检测如表2所示。
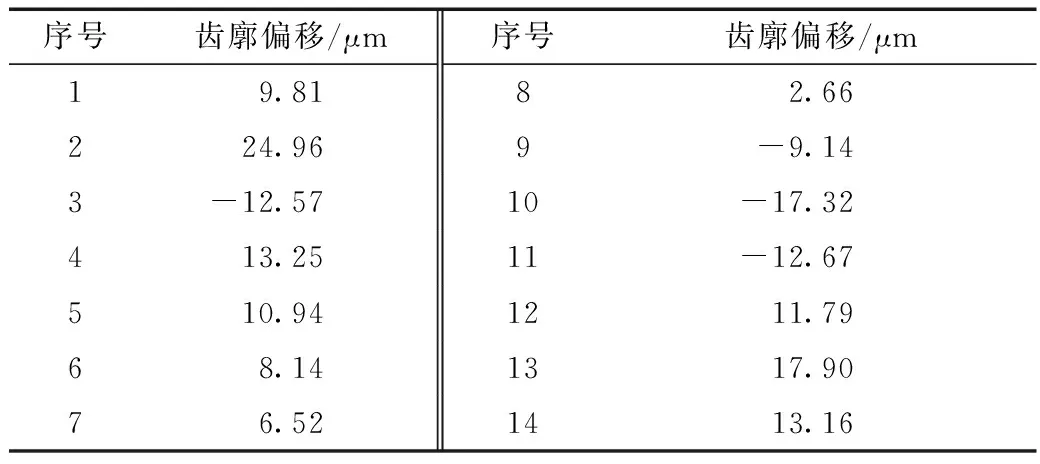
表2 齿廓偏差测量结果Table 2 Measurement of the tooth profile deviation
根据表2所列出的数据测量结果,齿轮齿廓偏移最大值为24.96 μm,最小为2.66 μm,考虑到齿廓参考点云的采集和配准时存在误差,取计算数据绝对值的平均值作为齿廓偏差,测量结果为12.20 μm。同时,依照该方法可对其他轮齿进行齿廓偏差计算。
一般工程中,对于被测齿轮进行齿廓评定指标仅需检查其齿廓总偏差,根据模数m=2和齿数z=23查《机械设计手册表》的“14-1-42”可知,所研究齿轮齿廓精度应不大于15.0 μm,对照检测值与查表所得值近似,并在合理的范围内,符合齿轮的精度等级,验证所采用方法可行性和准确性。
5 结论
论文采用计算机图形学的方法建立标准齿轮模型并提取数据获得齿轮的参考点云Z;利用机器视觉的方法在线拍摄齿轮图像并进行图像处理,借鉴Zernike矩算法获得清晰的亚像素齿廓边缘;去除齿廓边缘中的齿顶、齿根数据提取齿廓数据获得齿轮的目标点云W;分析了ICP算法在点云配准中的应用,并对参考点云Z和目标点云W进行点云配准;点云配准后,利用多项式拟合参考点集获得拟合曲线,计算目标点云中各点到拟合曲线的距离取平均值即为齿廓偏差。结果表明所提出的方法具有合理性,可重复性且满足齿轮的精度要求。
