“思维导图”在小学数学教学中精致化应用
2020-01-18刘丽
刘丽
摘 要:“思維导图”是一种“形象、高效的可视化学习工具”。借助思维导图,能促进学生的数学理解,能促进学生的思维沟通,能促进学生的实际应用。通过数学思维,学生的数学学习从零散走向集约、从粗放走向精致、从朦胧走向清晰。数学思维导图,有效地提升了学生的数学学习力,发展了学生的数学核心素养!
关键词:小学数学;思维导图;数学理解;思维沟通;实际应用
“思维导图”又被称为“心智地图”“脑力激荡图”“灵感触发图”等,是一种“形象、高效的可视化学习工具”。有隶属关系、层级关系等的一种思维支架。通过“思维导图”,学生不仅能认识到“学什么”,更能形成“怎样学”的思路。在数学教学中,教师要充分应用思维导图,去盘活学生的数学思维,去激活学生的数学学习潜质,去打通学生的问题解决思路等。通过思维导图,不仅可以促进学生的数学理解,而且可以促进学生的数学创新。
■一、思维导图,促进学生的数学理解
“思维导图”被称为“头脑的使用说明书”,思维导图的特点就是能形象地将数学知识的节点、脉络等展示出来,促进学生的放射性思维,进而促进学生的数学理解。“思维导图”的鼻祖托尼·博赞先生盛赞“思维导图”是一把“瑞士军刀”,能引领深度思维。小学生的数学思维是从直观动作思维过渡到具体形象思维的阶段,因而在数学教学中应用思维导图,契合学生的认知特质和心理特点。借助思维导图,不仅能将外在的问题题意表征出来,更能将学生不可视的思维敞亮开来。
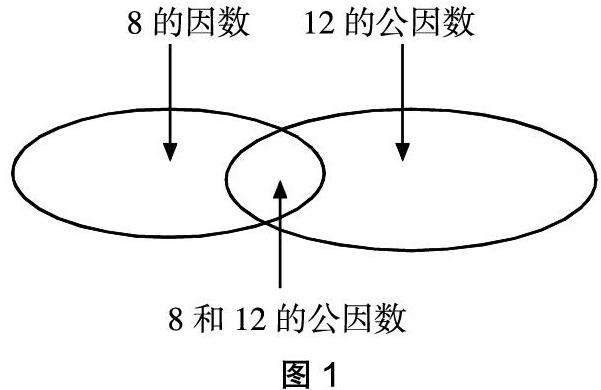
在数学教学中,笔者发现许多学生对问题的感知是蜻蜓点水、浮光掠影的,是比较肤浅的、机械的。如何激活学生的感知,促进学生对数学问题的理解?笔者认为,一个重要的方式就是借助思维导图对问题进行直观化、形象化地表征,从而让学生的数学思维有迹可循、触手可及。比如教学“约分”一节中的“最大公因数”(人教版五年级下册),为了促进学生的数学理解,笔者先让学生分别列举8的因数、12的因数,在此基础上找寻8和12公有的因数。但在教学中,笔者发现许多学生不理解“公有”这个词语的意思。为此,笔者用类似“韦恩图”的图形表示,重点出图是两个椭圆中的重复部分(见图1),引导学生认识到“公因数1、2、4”既是8的因数,又是12的因数。这样,将学生难以理解的、抽象的文字转化成学生易于理解的、直观的思维导图。通过韦恩图,学生不仅能找出两个数的“公因数”,还能找出两个数各自的独有因数,找出两个数的“最大公因数”,更能找出几个数的“公因数”“最大公因数”,等等。这样,思维导图不仅调动了学生数学学习的主动性、能动性,帮助学生解决了问题,而且悄无声息地渗透了数学思想方法。
应用“思维导图”,可以呈现学生的学习结构。学生根据思维导图中的关键词、中心词以及连线、箭头等,能深刻理解相对比较抽象的数学概念。在数学教学中,通过思维导图可以关照数学知识的重难点,可以关照学生数学学习的疑点、盲点、障碍点等。正如著名的物理学家、思想家爱因斯坦所说,“我不用语音思考问题,而是运用一幅幅能动的、跳动的图像来思考”。思维导图,能促进学生的知识理解,有助于学生对数学知识进行自主性的建构。
■二、思维导图,促进学生的思维沟通
思维导图的种类很多,比如常见的韦恩图、线段图、树形图、集合图等。思维导图与人脑是相互匹配的。比如思维导图具有放射性,而心理学、生物学研究表明,人脑电波、人类的思维也是放射性的。当外界的一个信息、讯息进入人的感官,被人脑捕捉到之后,人的感觉、记忆、思维、想象等都会在一瞬间激活。因而,应用思维导图,可以促进学生的思维沟通,比如直观思维与抽象思维的沟通,灵感思维与形象思维的沟通,等等。
比如教学“运算定律”(人教版四年级下册),笔者借助思维导图的“全开放性”“半开放性”等特性,引导学生进行完形填空,调动学生的数学思维,催生学生的数学想象。比如在教学“加法交换律”这一看似最为显明的运算定律时,笔者由浅入深,引导学生逐步抽象、概括出加法交换律。比如从“李叔叔今天上午骑了40千米,下午骑了56千米”中引导学生列出两种算式,即“上午骑行的千米数+下午骑行的千米数”,或者“下午骑行的千米数+上午骑行的千米数”。在此基础上,用这样的导图——“_____+_____=______+______”——引导学生举例。通过多元举例,为学生的猜想以及不完全归纳奠定坚实的基础。几乎所有的学生都用自己的方式表达了对“加法交换律”的猜想,比如用文字表达:甲数+乙数=乙数+甲数;用符号表达:△+○=○+△;用字母表达:a+b=b+a。借助“半随机半确定”“半混沌半有序”“半直觉半逻辑”“半归纳半演绎”的思维导图,让学生积极地进行补白,展开全方位、多角度的联想。不仅如此,“加法交换律”的教学为学生学习“加法结合律”“乘法交换律”“乘法结合律”“乘法分配律”奠定了坚实的知识、方法、探究基础。
思维导图,让我们仿佛看到了学生大脑神经元的无数突触,仿佛看到了思维神经元的多元联结。借助思维导图,学生的多元思维相互交织、自由绽放、深度绽放,从而能完成对数学知识的抽象、动态的保证。思维导图,让学生的思维变得触手可及,变得有迹可循。思维导图,能让学生的数学思维产生旋涡、产生风暴。借助思维导图,学生“友善用脑”“和谐用脑”“健康用脑”,从而让学生的数学思维、数学思考、数学思想从浅陋走向深刻,从简单走向复杂。
■三、思维导图,促进学生的学习应用
思维导图,不仅能促进学生的数学理解,促进学生的思维联结、思维发散,更能促进学生数学学习的具体运用。要抓核心,重积累。在学生应用的关节点、困顿处、繁难处都可以运用思维导图。思维导图是学生数学学习的一面镜子,能牵引、映照学生的数学学习。思维导图不仅是一种学习方法、策略,更是一种学习理念、思想。“思维导图”是一种“有意义的向导”,具有互动性、生成性。在思维导图这只“看不见的手”的牵引之下,学生的数学学习能变得灵动起来。
比如教学“圆的周长”(人教版六年级上册)一课后,有这样一个应用性的问题:“甲乙两地相距157米,一位学生用直径为1米的铁环从甲地滚向乙地,能滚50圈吗?”这个问题,从表面上看是一个简单的运用“圆的周长”的计算公式、方法去解决的实际问题。在学习应用中,全班学生都是先求出圆形铁环的周长,然后绝大多数学生都认为能够滚50圈。如何促进学生科学、理性地进行数学应用?依靠教师的言语说教是无济于事的。为此,笔者画出了思维导图,用其再现铁环滚动的场景。当笔者画出圆形铁环时,不少学生恍然大悟:圆形铁环滚动一周应当是从圆周上的某一点开始,还要回归到这一点,这是在探究“圆的周长”的计算公式做数学实验时达成的数学共识。这里,通过思维导图,学生自识其陋:圆形铁环的出发点、停止点都是距离甲乙两地0.5米处。真正的圆形铁环的转动圈数,应当将着眼点放置到圆形铁环的圆心上。圆心移动多少米,铁环就前进了多少米。思维导图,让学生在数学知识的运用中能主动地进行分析、类比、想象、判断、反思等深度的思维活动。通过思维导图,能突破学生的数学认知困顿,能突破学生数学应用的阀域,从而让学生的数学学习向纵深推进、发展。
“思维导图”是学生数学应用的“导航仪”,指引着学生数学应用的“路线”“方向”。通过思维导图,学生能触摸到数学知识应用的关键节点,触摸到学生数学知识应用的生长节律。思维导图,能解放和舒展学生的思维触角,让学生的数学思维紧紧贴合、扣牢应用情境,从而让学生的数学知识应用能力得到有效提升。
思维导图不仅仅是一种认知策略,更是一种元认知的策略。思维导图,是可视化教学的利器。将“思维导图”应用于小学数学教学中,要充分发挥其自主性、直观性、互动性的价值。思维导图有助于发展学生的数学深度思考力,有助于发展学生的数学深度探究力,有助于引导学生自主学习、自觉学习。思维导图,犹如一个桥梁,能够有效地嫁接数学知识、学生思维和实际应用,从而让学生的数学学习从零散走向集约、从粗放走向精致、从朦胧走向清晰。数学思维导图,能有效地提升学生的数学学习力,发展学生的数学核心素养!
