有向网络中节点层次挖掘与链路方向预测

冯 旭，虞志刚，赵 晶，陆 洲

(中国电子科学研究院，北京 100041)

0 引 言

近年来，随着信息技术的迅猛发展，人类社会大步进入网络时代。复杂网络将系统中的个体抽象为节点，将个体之间的关联或依赖关系抽象成节点之间的边，继而构造出表征系统的网络。作为研究复杂系统的有力工具，复杂网络广泛地用于各种真实网络数据的分析和建模，包括WWW、Internet、电力网络和交通网络等。近年来，我国正积极开展天地一体化网络的研究与发展工作，节点层次与链路特性挖掘对网络拓扑设计与优化具有重要参考意义[14-15]。层次广泛存在于复杂网络中[1,3]，并有着宏观和微观两方面的含义。宏观方面，层次是一种网络自身的重要特征，网络的层次属性是指网络中的节点可以划分为不同的群组，而这些群组又可以进一步划分为多个子群组的集合。微观方面，层次亦可作为一种节点的属性，表示了节点在网络中的地位。无向和有向网络都有着宏观上的层次特征，而作为节点属性时，层次的研究主要是在有向网络中。本文中，我们关注于层次的微观含义，即将有向网络中的节点层次视为节点的自身属性，其在多种类型的复杂网络中有着不同的含义。在社会学中，分层(Stratification)[1]是指按照一定标准将人划分为不同的等级(Hierarchy)或状态(Status)，层次现象广泛存在于不同组织和系统。社交网络中，人们会感知到其自身层次及与其连接的周围用户层次，同时用户在建立社交关系时也会考虑到这些局部的层次或状态信息。因此，基于观测到的网络结构，可以推断出网络中用户具体的层次值，有助于进一步理解用户在网络中的地位和功能。从复杂网络的研究角度看，层次可以视为网络中节点中心性的一种度量方式，因此一些已有的节点中心性指标对层次发现问题具有很好的启发意义。此外，层次还与链路挖掘中的节点排序任务紧密相关，其中层次发现更多地利用网络局部结构信息，而节点排序则主要从全局角度评估节点的重要性。

有向网络中节点层次度量旨在利用当前已知的链接信息，推断潜在的节点层次属性，有助于我们深入理解有向网络中链接的形成机理。层次度量吸引了来自计算机和物理等研究领域的关注。Gupte等人[1]定义了一种有向社交网络中的层次度量，并且给出了一个用于计算网络最优层次的多项式时间算法，作者还利用计算出的用户层次对多个真实社交网络数据进行了分析。Maiya和Berger-Wolf[5]将层次视为社交网络的概率生成模型，基于极大似然法从加权社交网络中推断用户具体层次。Rowe等人[4]基于响应时间和消息数目定义了一个邮件网络中的加权中心性指标，并于实际数据中进行了测试。Vicsek等人[3]提出了一个衡量网络层次的定量指标，该指标的定义基于“可达中心性”概念，实验表明该指标与网络可控性相关。Guo等人[2]将节点层次定义为节点的重要性排序值，提出一种基于入度和出度差的子图递归方法，对网络中所有节点进行排序，节点排序值可作为其层次的表示，并进一步用于有向边的方向预测。此外，节点层次度量与图论中的拓扑排序问题紧密相关，在一个可以给出拓扑排序的有向图中，节点的排序值即可作为层次度量的一种可行方案。本文中，我们首先给出节点层次度量问题的明确定义，并从理论上对问题复杂度进行分析。考虑到问题的复杂程度和当前大部分有向网络规模很大的情况，我们提出了一个有效的启发式层次度量算法。最后，从节点层次与有向链路一致性和有向网络链接方向预测两方面，我们设计了几个真实网络上的实验，实验结果表明了本文算法的有效性。

1 问题定义与分析

1.1 节点层次定义

给定一个有向网络G=(V,E)，其中V表示节点集合，E表示节点间有向关系集合，节点i和j之间的有向边用e(i,j)表示。层次度量可以认为是定义在节点集合上的映射函数H:V→N，即为图中每个节点赋予一个整数值表示该节点层次，在得到的节点层次集合中，对于任一节点i∈V，Hi表示节点i的层次值。有向网络中，我们认为节点层次与有向边方向存在关联性，节点建立有向关系时受其感知的自身和对方节点层次影响。层次较高的节点与层次低的节点间建立有向边的概率较低，因此层次度量的目的在于使得网络中大部分有向边方向从低层次节点指向高层次节点。

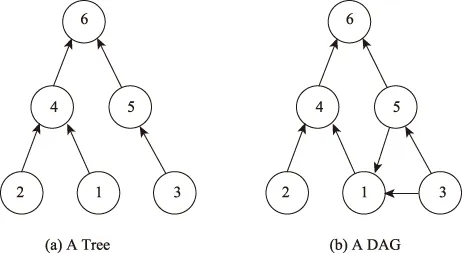
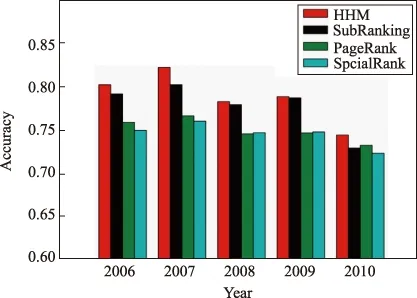
假设在某一层次度量H下得到了当前网络节点层次集合，将有向边e(i,j)与层次度量H的一致性以ce(i, j)表示。当Hi

ce(i,j)=I(Hi,Hj)，

网络与层次H的一致性C(G)定义为全部有向边一致性的和，即

在大多数实际情况下只能观测到有向网络的边结构，而节点层次属性是隐含其中的，我们需要从所有可能的层次度量中推断出与当前网络结构最一致的节点层次集合。因此，层次度量问题是为已知的有向网络找到一个具体的节点层次表示，使得与层次一致的有向边数目最大化。具体来说，网络层次h(G)定义为：

1.2 复杂度分析

如果存在某一层次度量H，使得节点层次与网络中所有边的方向是一致的，我们说网络G有着完全层次结构，即C(G)=|E|，也就是说，节点层次度量问题的上界是使得网络一致性等于边的数目。树和有向无环图(DAG)是有着完全层次结构的，如图1所示，图中数字表示节点号。对于树形结构来说，将叶节点层次值设为1，中间节点层次值为其子树节点中最大层次值加一，则图1树型结构网络中可得到以下层次集合{H1=1,H2=1,H3=1,H4=2,H5=2,H6=3}，其所有边与该层次都是一致的。对于无环有向图DAG，可以通过拓扑排序的方法找到一个与所有有向边一致的层次结构。如对于下图中的DAG来说，为入度为0的节点赋予层次值1，之后可以通过不断地删除入度为0节点并为节点赋予加一层次值，得到层次集合{H1=3,H2=1,H3=1,H4=5,H5=2,H6=5}。

图1 有向网络层次示例

但是现实中几乎全部有向网络中都存在环路，在网络中存在环路的情况下，易知不存在一个层次结构与所有有向边一致。如图2所示，节点1、2和4构成一个环路，无论如何进行层次赋值，三节点间的环路上至少有一条边与层次不一致。此外，在特定层次度量下，所有与该层次一致的边组成的子图一定是无环的，因此，层次度量问题等价于找到网络的最大DAG子图。精确求解网络最大DAG子图可分为两个步骤：第一找到网络中所有的环路；第二从环路的组成边中找到最小的边集进行删除以打破网络所有的环路。假设我们找到的环路集合为LOOP={l1,l2, …,lc}，其中每个环路li又可以表示为构成环路的有向边集合，即li={ei1,ei2, …,eik}，其中k表示环路li的边数。以图2所示为例，图中存在两条简单环路，其组成边的集合分别为{e(1, 2),e(2, 4),e(4, 1)}和{e(1, 3),e(3, 4),e(4, 1)}，其中删除边e(4, 1)可以打破两条环路，在所得DAG子图上的层次结构与剩余边都是一致的。针对网络中简单环路的发现问题，Tarjan[6]提出了一个较为有效的算法，时间复杂度为O((n+e)(c+1))，其中c是网络所有环路数目。而从网络中删除最少数目的边来打破所有环路也即发现最小反馈弧集(minimum feedback arc set)，是一个典型的NP难解问题[7-8]。事实上，即使以贪心策略选择最小边集来打破环路，找到有向网络中所有环路亦是十分困难的，因为环数c可能是网络节点规模N的指数级。此外，考虑到当前研究中的大规模网络数据，我们亟需提出一个高效的启发式算法来解决这个问题。

图2 有向网络层次示例

2 启发式层次度量算法

2.1 层次度量性质

根据上一节问题分析可知，层次度量等价于网络的最大DAG子图发现问题，其可以通过删除最少数目有向边以打破所有环路来解决。本节中，我们从环路与强连通分量(SCC)之间的关系入手，提出一个基于有向边删除得到DAG子图，并进一步在子图上度量节点层次的算法。

性质1：网络中任一环路的所有节点都属于同一强连通分量，不同强连通分量间的有向边不存在于任何环路中。

对于由节点集合{i1,i2, …,ic}组成的环路lc来说，其中任意两点都是相互可达的，因此，所有节点都在同一强连通分量中。同时，若节点i和j不在同一强连通分量中，则i和j之间必定不存在环路，因此若不同连通分量间有向边e(i,j)存在时，其必不属于网络的任何环路。根据此性质，我们可以通过将网络划分为不同的强连通分量，而强连通分量之间的有向边得以保留，并进一步在强连通分量内部进行删边过程。通过以上分析，我们将删边打破环路的过程集中在网络的每个强连通分量内部。假设我们已经得到网络的最大DAG子图并进行层次度量，则对于每一条被删除的边e(i,j)来说，在DAG上的的层次度量H下一定有Hi≥Hj。这是因为如果被删除的边e(i,j)与最大DAG子图上的的层次度量H一致的话，则将e(i,j)加入DAG依然保持其无环特性，因此与最大子图性质冲突。由此可知，在SCC内部删除的边应该是从层次较高节点指向层次较低节点的边，也就是说我们需要对节点层次进行预先估计。受有向网络中D-core指标[9]启发，我们考虑如下过程：设当前强连通子图节点集合为S，按一定顺序依次从当前节点集合中选出可能层次最低的候选节点进行移除，并依照节点移除顺序为其赋予从低到高的层次值。当从S中移除层次值可能最低的候选节点i时，当前S中所有指向i的边e(·,i)与该层次赋值不一致，而i指向其他节点的边e(i, ·)则与层赋值次一致，也即：

以上性质说明在强连通子图内，我们应当选择入度小而出度大的节点赋予较低的层次。因此，我们根据节点的入度与出度差将当前节点集合S分为LOW和HIGH两个子集，并移除从HIGH中节点指向LOW中节点的有向边，之后在各自内部继续执行以上删边过程。

2.2 HHM算法

综合以上分析，我们提出了一个基于删除最小数目边得到DAG子图，并于子图内进行拓扑排序的启发式层次度量算法(HHM)，其过程如算法1所示。首先，HHM根据Tarjan算法[10]将当前网络划分为不同的强连通分量(SCC)；之后在每个SCC内部进行删边以打破其中的所有环路。Delete(SCC)表示对强连通子图SCC内部删边的处理，如算法2所示。首先，根据入度和出度的差值将节点分为LOW和HIGH两个集合并删去HIGH集合中节点指向LOW集合中节点的有向边；之后在LOW和HIGH中节点构成的子图中继续划分强连通分量并重复以上删边过程。在将某一强连通分量划分为LOW和HIGH两个子集时，可以设定参数来表示其规模比例，本文中我们选择均分方案，即使得LOW和HIGH 集合有大致相等的节点数目。通过以上过程我们会得到一个原网络的DAG子图，在DAG图中通过不断地删除入度为0的节点并更新节点邻居的出度，便可以得到所有节点上的层次值。

算法1：启发式层次度量(HHM)

输入：有向网络G=(V,E)

输出：节点层次集合H

将网络划分为强连通子图的集合SCCs←Tarjan(V);

for每个强连通子图 SCC∈SCCs: do

Delete(SCC);

end

当前层次值h= 0;

while True do

候选集合candidate初始为空集;

将所有入度为0的节点加入candidate;

foru∈candidate: do

Hu=h;

对所有节点w:u→w，对w的入度减一;

end

ifcandidate=Ø then

break;

end

else

h←h+1;

end

end

算法2：强连通子图内部有向边删除Delete(SCC)

输入：强连通子图 SCC

根据入度与出度差将SCC中节点分为两个子图G→LOW, HIGH;

将LOW划分为强连通子图集合SCCs←Tarjan(LOW);

for每个强连通子图 S∈SCCs: do

Delete(S );

end

将HIGH划分为强连通子图集合SCCs←Tarjan(HIGH);

for每个强连通子图S∈SCCs: do

Delete(S );

end

Delete Edge from HIGH→LOW;

3 实验及结果分析

本文中我们为有向网络节点层次度量提出了一个基于删边的启发式算法，本节中在实际有向网络中验证算法有效性。此外，通过删除一定比例的有向关系，我们将节点层次应用到有向边方向预测中。最后，我们在一个实际的时序数据上验证有向关系生成与节点层次的关系。

3.1 实验数据

为了验证本文提出算法的有效性，我们选择了四种不同领域的真实有向网络进行实验，分别是：(1)C.elegance神经网络,节点为神经元，有向边表示信号在神经元间的传导[11]；(2)PoliticalBlog博客网络，有向边表示两博客间存在引用关系[118]；(3)WikiVote，维基网站中2008年以来的选举网络[12,13]；(4)Ciao评价网络，有向边表示Ciao网站中用户间信任关系[139, 140]。四个有向网络的基本特征如表1所示，从中可以看出，与双向关系相比，网络中大多数节点间是单向连接的。

表1 有向网络数据及其基本特征

为了验证HHM算法有效性，我们选择了相关领域的几种对比方法，分别是：

(1)PageRank：PageRank是信息检索领域的一个重要算法，其利用随机游走的思想，最早用于对网页重要性进行排序。本文中，我们利用PageRank算法为有向网络中的每个节点赋予一个权值，并以此权值作为节点层次值。值得注意的是Pagerank算法赋值并不是整数，由于我们在分析节点层次与边方向一致性时只关注节点间层次值的相对大小，因此非整数赋值对实验结果没有影响。对于网络中每个节点i，其Pagerank值由下式所得：

其中Pt(i)是随机游走在t步访问到节点i的概率，每一步中随机游走以概率c沿当前节点的邻居进行转移，并以概率1-c跳到一个随机节点，实验中c取值为0.85。初始状态下随机游走位于每个节点的概率是相同的，为1/N，我们以随机游走到达节点的稳定概率作为该节点的PageRank值，也即节点层次值。

(2)SubRanking：Guo等人[2]认为节点重要性与其局部链接结构更为相关，因此将网络不断划分成为更小的子图，并于子图内对节点重要性进行排序，本文中我们将其方法记为SubRanking。

(3)SocialRank：在特定层次下，Gupte等[1]定义边上损失

Agony(e(i,j))=max(r(i)-r(j)+1, 0)，

其中r(i)为节点层次值，而网络层次为所有边上损失和最小的情况，基于此定义作者提出了一个多项式时间算法从网络中推断层次，记为SocialRank。

在接下来的实验中，我们分别从层次度量与网络一致性和有向边方向预测两方面将HHM算法与以上几种方法进行对比。

3.2 节点层次与网络一致性

首先，我们比较四种方法确定的节点层次与不同网络结构的一致性结果。从有向边与节点层次一致性定义中可以看出，互惠关系中的两条单向边至多只能有一条满足某层次度量下的一致性。因此，我们在计算节点层次与网络结构一致性时只考虑单向关系节点对上的结果，即网络层次h(G)只计算单向边中的情况。以EU表示E中的单向边节点对集合，则一致性指标Conformity定义为：

从表2中可以看出本文算法HHM为节点赋予的层次值与四种网络有向结构都是是最为一致的，说明HHM算法能够有效利用网络中的已知结构，对节点隐含的层次进行推断。

表2 节点层次与网络一致性

3.3 有向边方向预测

为了进一步说明层次如何应用于实际的有向网络任务中，我们进行有向边方向的预测实验。首先，我们从网络中观测到的单向有向边中选择一定比例删除，记为EP，剩余边记为ER。在ER上运行几种算法对节点层次进行度量，依层次预测EP边的方向，正确预测集合记为EC，定义准确率为：

我们首先在四个静态网络上进行预测实验，其中移除有向边的比例为20%。预测结果如表3所示，HHM在C.elegans、PoliticalBlog和WikiVote三个网络中都取得了最高的预测准确率，在Ciao网络中SubRanking的预测效果最好。

表3 节点层次与网络一致性

此外，我们还利用Epinions信任网络进行有向边方向预测实验。在该网络中，节点间的有向关系有建立的时间信息，因此，与静态网络中随机移除有向边方向不同，在Epinions中我们按时间顺序对较晚出现的单向关系方向进行预测。具体来说，Epinions信任网络节点数为91748，有向边数为577926，边的建立时间为2005年至2011年。在链路方向预测实验中，分别选择2006年至2010年间每年新生成的单向边作为预测集合，以选定时间之前的数据作为已知网络并分别利用四种层次度量方法进行节点层次的计算。

预测结果用准确率进行评价，如图3所示，与其它三种方法相比，HHM在每一年的边方向预测中都取得了最好的结果。其余三种对比方法中，SubRanking 的效果较好，而PageRank和SocialRank的准确率大致相同。

图3 Epinions网络中边方向预测准确率

4 结 语

本文中，我们研究有向网络中节点层次与链路方向之间的关联。根据已有层次理论和节点排序方面的研究结果，节点建立链接的过程中受其自身层次属性的影响，因此利用已知的网络结构可以对隐含的节点层次信息进行推断。论文首先从形式上定义有向网络中层次度量问题，并分析了精确求解算法的复杂度。之后提出一个基于删边的启发式层次度量算法，通过在真实网络与几种已有方法进行对比可知，本文提出的算法可以有效地发现与网络结构一致的节点层次；进一步将节点层次地应用到有向链路的方向预测问题，在静态和演化网络上都取得了较好的效果。

本文对节点层次度量定义时只考虑了节点层次与网络中单向关系的关联，而互惠关系也体现了节点层次的影响，未来研究方向包括建立符合单向和互惠关系的节点层次模型。此外，节点在网络全局和局部结构中的层次亦不尽相同，因此将节点层次与其社团属性相关联，发现节点在不同局部结构中的作用也是需要研究的一个重要问题。