一种极坐标系下的激光雷达扫描匹配SLAM方法

雷道竖,刘海波

(1.河南省航空物探遥感中心,河南 郑州 450053;2.常州机电职业技术学院，江苏 常州 213164)

0 引 言

近年来，激光雷达(Light Detection and Ranging, LIDAR)因其便利、快速、准确等优势，在航天、林业、气象等领域得以广泛应用[1-4]。随着智能机器人技术的发展，激光测距雷达在室内结构化未知环境的即时定位与地图构建(Simultaneous Localization and Mapping, SLAM)上发挥着越来越重要的作用[3-4]。

现有的SLAM技术主要可分为基于概率和基于扫描匹配的方法。其中，基于概率的方法包括基于卡尔曼滤波和基于粒子滤波的方法[5]。基于卡尔曼滤波的方法目前在SLAM技术中应用最为广泛，但是随着时间状态维数的增加，该方法计算量显著增大，并且难以有效解决闭环回路问题。基于粒子滤波的算法能很好地适用于非线性模型，有效解决闭环回路问题，但是存在粒子重采样及粒子衰竭等问题。基于扫描匹配的SLAM算法较为简单，其基本思想是匹配相邻两帧扫描数据解算两者之间的2维姿态转换矩阵从而更新平台位置实现地图的创建与自主导航[6-7]。

目前大部分的扫描匹配都是通过迭代实现的，如Interactive Closest Points (ICP)及其改进算法等[8]。ICP算法通常用于点与点的局部匹配，尽管许多学者对ICP算法进行了研究改进，但这些算法都需要通过最近邻搜索等方式预先构建有效的点集对应关系。进而在确定的对应关系的基础进行迭代，获取最优解。因此，基于ICP的方法运算量较大，实时性较差，限制了该方法在SLAM技术中的有效应用。

室内环境中存在广泛的直线段特性[6]。这些特性的引入和利用可以有效提高扫描匹配的效率和性能。文献[6]基于线段、角点等几何特征实现室内激光雷达的扫描匹配，取得了较好的效果。本文利用室内扫描数据中的线段特性，提出了一种极坐标系下的激光雷达扫描匹配方法。与以往在空间坐标系下的线段匹配方法不同，本文直接在极坐标下描述扫描数据中的线段特征以及构建最终的匹配代价函数。这种方法有效避免了空间坐标系下对点集的对应关系的要求。针对极坐标系下的扫描特性，采用周边环境面积函数进行描述。该函数描述了测量平台在室内不同位置时各个角度下的距离测量分布。最后，在极坐标系下通过相邻扫描之间的线段特性构建匹配代价函数。线段特性的引入使得最终需要优化的匹配代价函数具有良好的解析形式，从而大大提高了优化求解的效率和精度。通过优化目标函数，获得两幅扫描数据之间的2维姿态变换矩阵，实现未知环境中地图的更新和创建。实验中，基于公开数据集对提出方法进行了验证，证明了其有效性。

1 极坐标下的扫描匹配的基本思路

如图1所示，激光雷达可以采集平台在室内某一位置时不同角度的距离测量值。平台在室内某一位置向周围各个角度发射激光，从而测量其到各个方向最近障碍物的距离。这些距离值的分布实际上就反映了平台当前在室内所处的位置。因此，通过分析比对两幅相邻扫描数据在不同角度下的距离分布可以求解它们之间的相对位姿关系，从而更新平台的位置。为了便于求解，本文首先定义周围环境面积函数如公式(1)所示。

(1)

其中F(φ)代表角度φ下的距离测量值；S为定义的周围环境面积。

此时，相邻扫描数据之间的匹配误差可以表示为：

(2)

其中F′(φ)代表变换后的扫描结果。Γ代表两条扫描之间的姿态变换矩阵，采用仿射变换的形式，如公式(3)所示。

(3)

其中θ代表旋转角度；tx，ty分别代表位置偏移量。

理论上，通过对公式(2)中的目标函数进行优化即可求出最佳的变化矩阵。然而，直接对公式(2)进行优化收敛速度很慢，不利于实现实时的地图更新。并且，复杂的目标函数容易陷入局部最优解，导致定位精度下降。因此，本文通过考察室扫描数据固有的线段特性提高优化求解的效率和精度。

2 极坐标下的线段描述

室内激光雷达扫描数据广泛存在线段特征。这些线段可以通过直线检测的方法得以获取[6,9]。通过利用这些线段特性可以有效提高扫描匹配的效率和精度。在极坐标系下，直线可以采用如下形式表达：

(4)

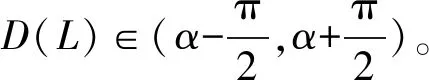
(5)

对公式(4)中的线段按照公式(3)中的变换矩阵进行仿射变换可以得到：

(6)

3 优化求解

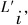
(7)

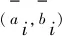
(8)

其中Pi(φ)定义如下：

(9)

最终，两幅扫描数据的整体匹配误差定义为所有线段的部分匹配误差之后，如公式(10)所示。

(10)

其中C为调和参数，定义如下：

(11)

相比直接从公式(2)获取姿态变换矩阵，线段特性的引入使得公式(10)中的目标函数形式更为简洁，便于后续的优化求解。本文采用经典的梯度下降法[10]最小化公式(10)中的目标函数从而求解最佳的姿态变换矩阵。由于目标函数具有良好的解析形式，此时梯度下降法可以较为迅速地收敛并获得全局最优解。

图2显示了在线段表示下两幅相邻的扫描数据的相对位置关系。图中的灰色区域代表两者之间的姿态偏差。通过采用提出算法进行优化求解，得到在最小误差时的匹配结果如图4所示。可以看出，此时求解的姿态变换矩阵很好地纠正了两者之间的误差。

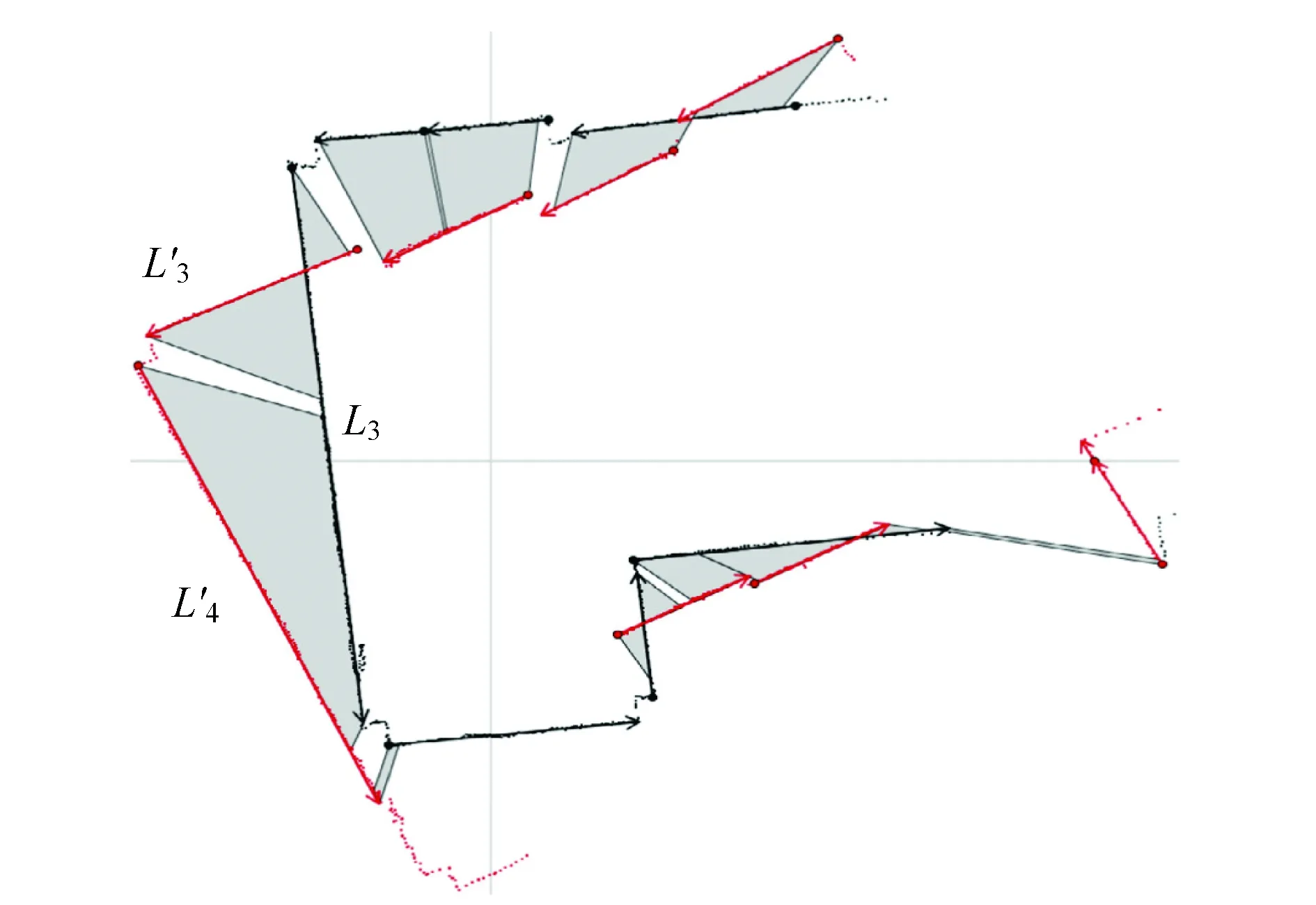
图2 相邻两幅扫描的相对位置关系(灰色区域表示它们之间的误差)

图3 采用本文方法优化得到的匹配结果

4 实验与分析

4.1 实验数据集

为了验证提出算法的有效性，本文采用公开的因特尔实验室(Intel Research Lab)数据集[11]进行了验证实验。同时，将提出算法与经典的ICP算法[8]以及文献[6]提出的基于几何特征关联的算法(记为几何关联)进行了性能对比。

4.2 实验结果与分析

采用三类方法分别对英特尔实验室数据集中的前1700幅扫描数据进行处理，得到的结果分别如图4中的(a)，(b)，(c)所示。根据图中的结果，选用的1700幅扫描数据可以显现出地图构建和定位过程中出现的累积误差。从图中可以直观得看出，本文算法的定位结果误差相对较小，并没有出现明显的错误。另外两类对比方法的累积误差相对较大。例如，对于图4(b)中ICP算法的结果，它在每一条扫描处均存在较大的误差，这也导致了地图绘制的开始和结束均存在一定程度的失配。

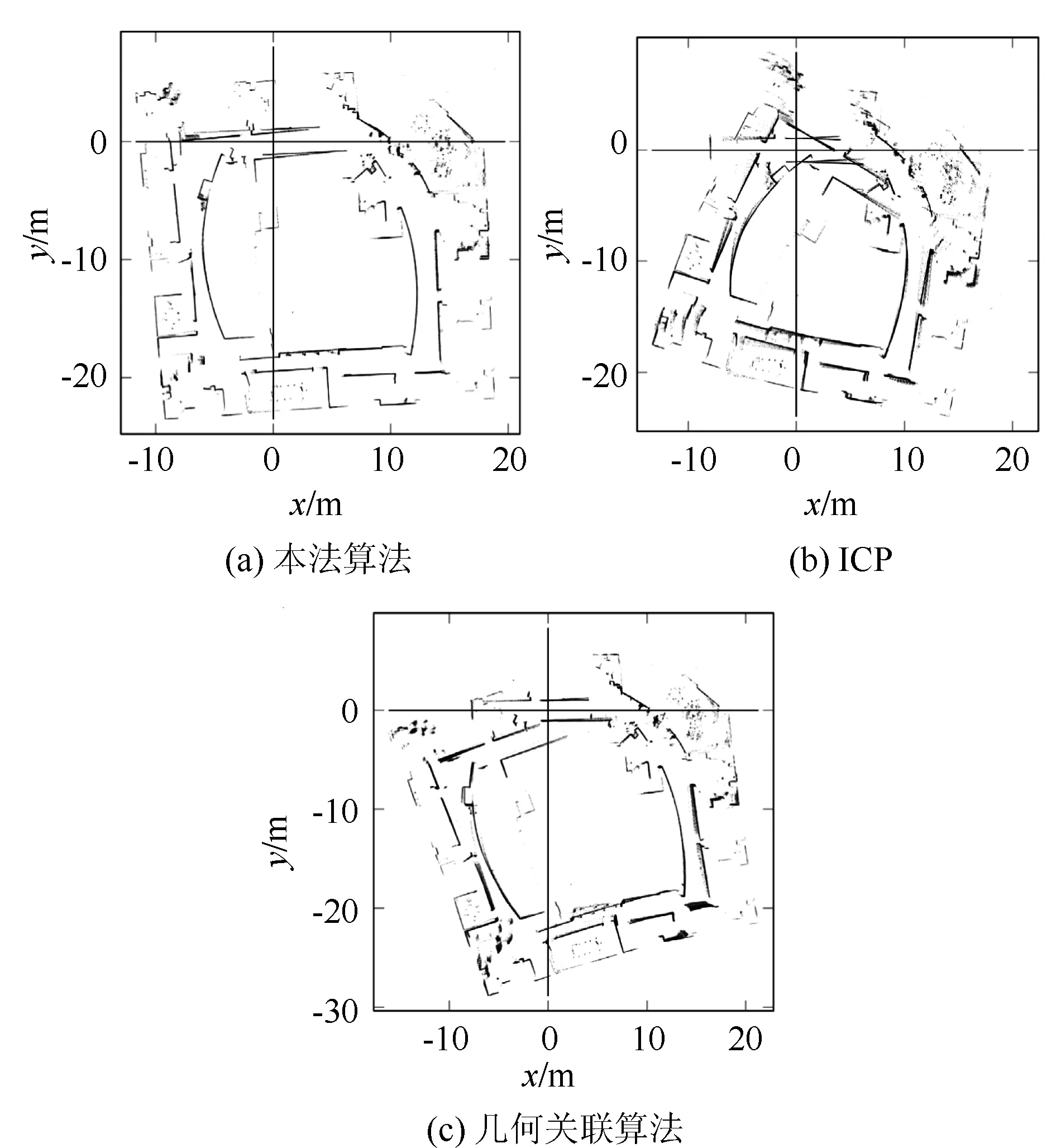
图4 不同算法上的定位结果

为了进一步体现本文算法的优势，图5显示了各类算法累积定位误差(与已知的真值对比求得)随扫描数目的变化曲线。对比而言，本文算法的累计误差始终显著低于其它两类方法，且随着迭代次数的增长率最低。这一结果表明提出方法在每一次的匹配过程中误差均较低，即每一次的匹配精度均达到了较高的水平。表1进一步对比了不同算法的平均时间消耗以及定位误差。可以看出，本文方法具有最小的时间消耗以及定位误差且显著低于另外两类方法。这是因为线段特性的引入使得后续的优化目标函数具有明确的解析表达形式，因此求解收敛加快从而提高了运算效率。同时，求解过程中，算法陷入局部最优解的可能性降低，因此定位精度也相对较高。

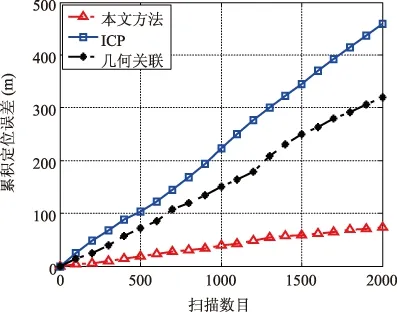
图5 不同算法的累计定位误差随扫描数目的变化曲线

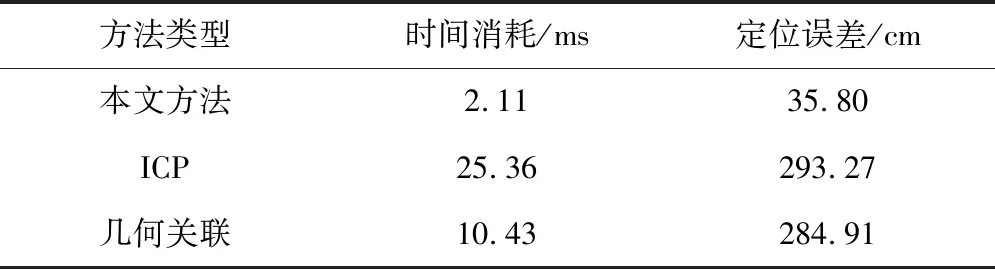
表1 各类算法的平均时间消耗和定位误差

5 结 语

本文提出一种基于极坐标系下激光雷达扫描匹配的SLAM算法。首先在极坐标系下设计了环境面积函数描述了平台在室内不同位置是的距离测量值分布，进而得到了求解姿态变换矩阵的目标函数。为了提高求解效率和精度，本文充分利用室内扫描数据中的线段特性。通过这一特性的引入，使得最终的优化函数具有明确的解析形式，大大方便了后续的优化求解。基于公开的英特尔实验室数据集进行了实验并与其它算法进行了性能对比，验证了提出方法的有效性。