关于2树子图的一些性质
2021-08-06曾德炎翟冬阳
曾德炎,翟冬阳
(三亚学院 理工学院,海南 三亚 572022)
1 2树子图
用Km,Km,n,Pk分别表示顶点数为m的完全图,m×n阶完全二部图,顶点数为k的路。设v∈V(G),X⊆V(G),用G[X]和NX(v)分别表示在G中由点集X诱导的子图和顶点v在点集X中的所有邻点构成的集合。记G-v=G[V(G)/v],G-X=G[V(G)/X]。文中未定义的标记参见文献[1]。

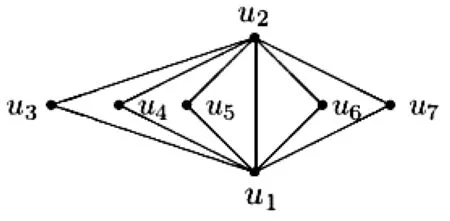
图1 7阶2树星图T(7)Fig.1 7 vertices 2-tree star map T(7)
若n≥3,定义F(n)是在F(n-1)的基础上增加一个新的点xn,并且连接xn-2xn,xn-1xn。显然F(n)也是一个n个顶点的2树,可以称它为2路。图2是F(7)。

图2 7阶2树F(7)Fig.2 7 vertices 2-tree F(7)
主要证明了下面两个定理:
定理1:设G是一个顶点数为n的2树,设X⊆V(G),其中|X|=k,3≤k≤n-1,则G中由顶点集X诱导的子图是某个顶点数为k的2树G1的子图。
对于k=n-1的情形,不仅证明了G1的存在性,并且找出了G1。
定理2: 设G是一个顶点数为n的2树,设xy∈C(G),其中xy被s个耳朵z,z1,…,zs-1粘贴。若n≥6,则G中由顶点集V(G)/{x,y,z}诱导的子图是某个顶点数为n-3的2树的生成子图。若n≥8,则G中由顶点集V(G)/{x,y,z}诱导的子图是某个顶点数为n-3的2树T的生成子图,并且T≠T(n-3)。
2 证明
为证明定理1和定理2,用到以下已知结论:
定理3[2]:设G是一个顶点数为n的2树。则:
(1)G中至少有两个耳朵;
(2)G中度为2的顶点是G的耳朵;
(3)G中不存在两个耳朵相邻,除非G=K3;
(4)G中不包含长度至少为4的无弦圈;
(5)G是一个2连通图。
定理4[3]:G中的每一条边都可作为基础,通过反复粘贴耳朵将G构造。
通过定理4,能很快构造出4个顶点2树且只有K4-e,也就是T(4),如图3。
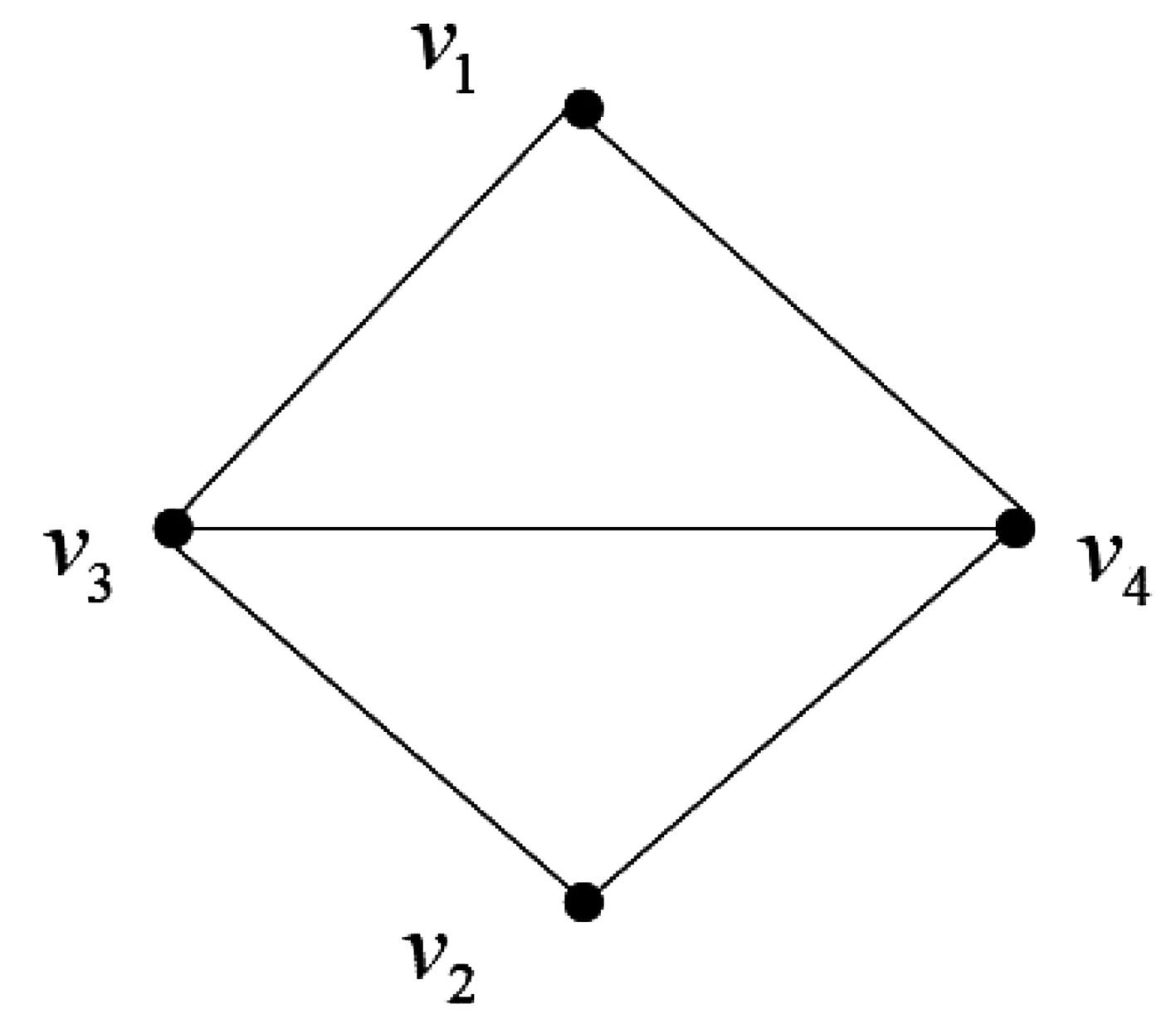
图3 唯一的4阶2树K4-eFig.3 Only 4 vertices 2-tree K4-e
5个顶点2树只有两个,分别是K5-K3和K5-P4。由于K5-K3=T(5),因此K5-P4是唯一一个非星图的5阶2树。图4是K5-K3,图5是K5-P4。

图4 5阶2树K5-K3Fig.4 5 vertices 2-tree K5-K3
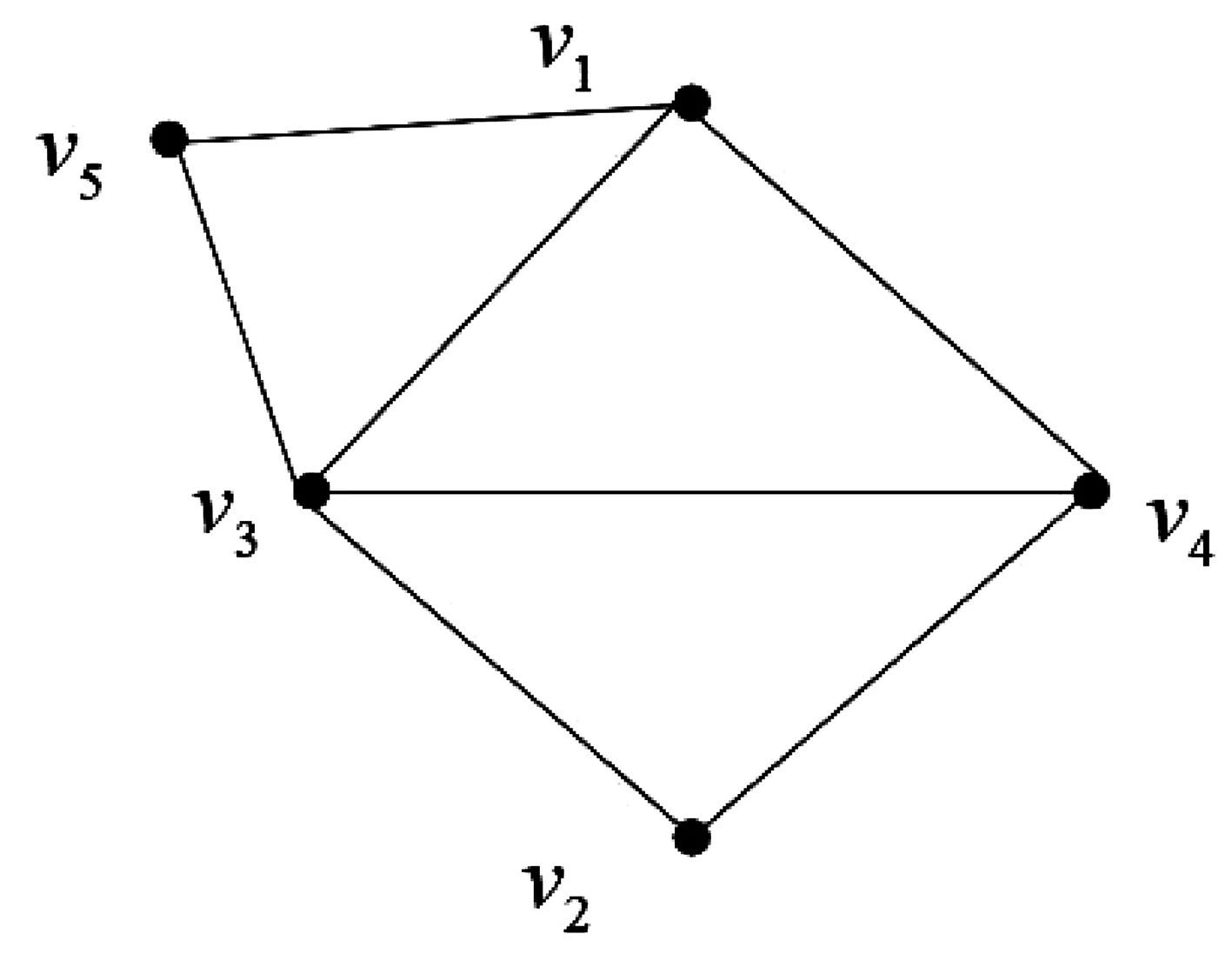
图5 5阶2树K5-P4Fig.5 5 vertices 2-tree K5-P4
同样的方法,构造出6个顶点的2树有5个,7个顶点的2树有12个。对于7个顶点的2树,有一些很易证明的性质:设G的一个顶点数为7的2树,则在G中能找到两个点x,y,使得G-{x,y}是P5的子图;在G中能找到两个点u,v,使得G-{u,v}是K3∪P2的子图;若G不是7个顶点的星图T(7),则在G中能找到一个顶点z,使得G-z是6个顶点的2路F(6)的子图。
为证明定理1和定理2,先证明下列会用到的引理:
引理1:设G是一个顶点数为n的2树,其中n≥4,设v∈V(G),则G-v是某个n-1阶2树的生成子图。
证明:对n用归纳假设法。当n=4时,由于三个顶点的2树只有一个K3,G-v显然是这个唯一的三阶2树K3的子图。也就是说当n=4时,引理1成立。假设n≠4,也就是n≧5。若v是G的一个耳朵,则显然G-v是一个顶点数为n-1的2树,因此G-v是某个n-1阶2树的生成子图。现在假设v不是G的耳朵,设u是G的一个耳朵。若v∈NG(u),记G1=G-u,则G1是一个顶点数为n-1的2树,并且G-v是G1的一个生成子图,从而G-v是某个n-1阶2树的生成子图。若v不属于点集NG(u),由于G-u是一个顶点数为n-1的2树,根据归纳假设可知G-{u,v}是某个顶点数为n-2的2树G2的生成子图。显然NG(u)是V(G2)的子集,并且NG(u)在G2中的诱导子图为K2。现在在G2的基础上增加一个新的顶点u,使得u与NG(u)中的每一个顶点都连边,得到的新图记为G3。显然G3是一个顶点数为n-1的2树,并且G3包含G-v作为子图。也就是说G-v是n-1阶2树G3的生成子图。引理得证。
引理2:设G是一个顶点数为n的2树,其中n≥5,设V′⊆V(G),其中|V′|=s≤n-3。则G-V′是某个n-s阶2树的生成子图。
证明:对s用归纳假设法。由引理1可知,当s=1时,定理2成立。假设2≤s≤3,设v∈V′。根据归纳假设可知G-(V′-v)是某个顶点数为n-(s-1)的2树G1的生成子图。由引理1可知,G1-v是某个顶点数为n-s的2树的生成子图。因为G-V′是G1-v的一个生成子图,所以G-V′也是某个顶点数为n-s的2树的生成子图。引理得证。
定理1的证明:设G是一个顶点数为n的2树,设X⊆V(G),其中|X|=k,其中k≧3。由引理1可知,定理1对于k=n-1的情形是成立的(令X=V(G)-{v}即可),证明了G中由顶点集X诱导的子图是某个顶点数为k的2树G1的子图。由引理2可知,定理1对于4≤k≤n-2的情形是成立的(令X=V(G)-V′即可)。证毕。
引理3:设G是一个顶点数为n的2树,其中n≥6,G≠T(n)。设B(G)是G中所有耳朵构成的点集,C(G)={e(u)|u∈B(G)},则|C(G)|≥2。
证明:若|C(G)|=1,不妨设C(G)={xy},则G中所有的耳朵都粘贴在xy上,即B(G)中所有的点都粘贴在xy上。因此G=T(n),矛盾。设G′=G-B(G),由于G≠T(n),有G′中的顶点个数大于等于3,并且G′是一个2树使得V(G′)-{x,y}中的每一个顶点的度均大于等于3,因此G′≠K3(2树K3中有3个2度点)。由定理3(1)可知,G′中至少有两个耳朵,即两个度为2的顶点,因此x,y是G′中有且仅有的两个耳朵,由定理3(3)可知,G′中的耳朵互不相邻,这与xy∈C(G)(若xy∈C(G),则xy是G中的一条边)矛盾。因此|C(G)|≥2。引理得证。
引理4:设G是一个顶点数为n的2树,其中n≥6,设xy∈C(G),其中xy被s个耳朵z,z1,…,zs-1粘贴,则G-{x,y,z}是某个顶点数为n-3的2树的生成子图。
证明:设G≠T(n),设G′=G-{z,z1,…,zs-1}。则G′是一个顶点数为n-s的2树。由C(G)中至少有两条边(引理3的结论|C(G)|≥2),有n-s≥4。根据定理4可知,G′可以在xy的基础上通过反复增加新的顶点,并且让这些新的顶点与图中的某条边的两个端点相连构造而成。在由xy构造G′的过程中,设y′是第一个顶点,让y′粘贴到xy上。因为xy在G′中没有被耳朵粘贴,所有y′在G′中的度大于2。因此xy′或yy′必须被至少一个新的顶点粘贴。设x′是第一个粘贴到xy′或yy′上的新顶点。不是一般性,设x′粘贴到了xy′上。设{x1,…,xt}是V(G′)的子集,其中x1,…,xt均粘贴到了xx′上。设{y1,…,yt′}也是V(G′)的子集,其中y1,…,yt′均粘贴到了yy′上。记
在G″中定义顶点x为顶点x′,定义顶点y为顶点y′,并且粘贴z,z1,…,zs-1到x′y′上,重新得到的图记为G‴。此时,G‴就是一个顶点数为n-3的2树,并且G-{x,y,z}是顶点数为n-3的2树G‴的一个生成子图。
若G=T(n),则G-{x,y,z}是一个顶点数为n-3的独立集。显然,此时G-{x,y,z}是任意一个顶点数为n-3的2树的生成子图。引理得证。
引理5:设G是一个顶点数为n的2树,其中n≥8,设xy∈C(G),其中xy被s个耳朵z,z1,…,zs-1粘贴。则G-{x,y,z}是某个顶点数为n-3的2树T的生成子图,并且T≠T(n-3)。
证明:记H=G-{x,y,z}。若s≥2,则G-z1是一个顶点数为n-1的2树,根据引理4,(G-z1)-{x,y,z}是某个顶点数为n-4的2树T′的生成子图。可以在T′的基础上新增一个顶点z1,让其粘贴到一条合适的边上得到一个顶点数为n-3的新2树T,使得T≠T(n-3)。显然,H是T的一个生成子图。因此,对于C(G)中的任意一条边xy均只被一个耳朵粘贴。对于这种情形,用反证法证明,即假设包含H作为生成子图的n-3个顶点的2树只能是T(n-3)。
设V(T(n-3))={u,v,w1,…,wn-5},其中uv∈C(T(n-3)),并且uv被n-5个耳朵w1,…,wn-5粘贴。若存在1≤p≤n-5,使得wpu∉E(H)。则H是n-3个顶点的2树T=T(n-3)-wpu+wpwq(1≤q≤n-5,q≠p)的生成子图。显然T≠T(n-3),矛盾。
因此对于任意1≤p≤n-5,均有wpu∈E(H)。同理可得,对于任意1≤p≤n-5,均有wpv∈E(H)。因此,若uv∈E(H),则H=T(n-3);若uv∉E(H),则H=K2,n-5。
如果H=T(n-3),|E(G)|=2n-3和|E(H)|=2(n-3)-3=2n-9,把G中由顶点集{x,y}与顶点集V(H)之间连接的边的数量记作eG({x,y},V(H)),则eG({x,y},V(H))=(2k-3)-(2k-9)-3=3。若|NH(x)|=3或|NH(y)|=3,则G显然不是一个2连通图,这与定理3(5)矛盾(即与G是2连通图矛盾)。因此|NH(x)|≤2,|NH(y)|≤2。记W={w1,…,wn-5}。设|NH(x)|=2或|NH(y)|=2,不失一般性,不妨设|NH(x)|=2,设wix和wjx是G中的两条边,则xwiuwjx在G中是一个长度为4的无弦圈,这与定理3(4)矛盾(即与G中不含长度大于等于4的无弦圈矛盾)。若|NH(x)|=|NH(y)|=1,设wrx和wty是G中的两条边,则xwruwtyx在G中是一个长度为5的圈。因为eG({x,y},V(H))=3,所以圈xwruwtyx中至多有一条弦,因此G中至少存在一个长度为4的无弦圈,这与定理3(4)矛盾(即与G中不含长度大于等于4的无弦圈矛盾)。若|NH(x)|+|NH(y)|≤1,则uv∈C(G)并且uv被粘贴n-5-1≥2个耳朵,这与C(G)中的任意一条边均只被一个耳朵粘贴矛盾。
若H=K2,n-5,则H中存在长度为4的无弦圈,从而G中存在长度为4的无弦圈,这与定理3(4)矛盾(即与G中不含长度大于等于4的无弦圈矛盾)。
因此,假设不成立,也就是说G-{x,y,z}是某个顶点数为n-3的2树T的生成子图,并且T≠T(n-3)。引理得证。
定理2的证明:设G是一个顶点数为n的2树,设xy∈C(G),其中xy被s个耳朵z,z1,…,zs-1粘贴。引理4证明了:若n≥6,则G中由顶点集V(G)/{x,y,z}诱导的子图是某个顶点数为n-3的2树的生成子图。引理5进一步证明了:若n≥8,则G中由顶点集V(G)/{x,y,z}诱导的子图是某个顶点数为n-3的2树T的生成子图,并且T≠T(n-3)。证毕。
