基于OFDM波形的机载雷达地面运动目标检测

柳丽召,王 力

(1.成都理工大学，四川 成都 610059;2.湖南理工学院，湖南 岳阳 414006)

0 引 言

检测环境开阔、背景强杂波、敌方电子设备的反侦察和干扰以及目标的雷达截面积(radar cross section, RCS)的起伏等问题，给地面运动目标检测带来了不小的挑战[1-2]。机载雷达的波形设计可以帮助改善地面运动目标的检测性能，其中正交频分复用(orthogonal frequency division multiplexing, OFDM)波形是一种有效的检测目标的波形方案。基于OFDM波形的信号有着对多普勒频移容忍度高的优点[3-4]，使之能更好地进行目标检测。OFDM波形可以增加系统的频率多样性以使不同的散射中心能提供更多的返回信息[5]，此外，它通过信号本身的频率正交性，可以利用单通道实现信号的发射接收，不需要硬件上的多个天线阵元，减少了实现成本，降低了操作复杂度。OFDM波形将传统的单载波发射信号调制到多个子载波上叠加后发射，可以增加系统的空间自由度[6]，从而具有被用于杂波抑制的潜力，甚至可以在抑制杂波以后估计目标的径向速度。

与线性调频信号(linear frequency modulation, LFM)相比较，OFDM信号的多普勒信息比同带宽的LFM信号要多[3]，不存在LFM信号的距离-速度模糊，具有良好的频谱利用率和动态分配能力[7-8]。另外，文献[9]和[10]指出基于OFDM信号的雷达系统能够提供很高的多普勒分辨率，可以很好地解决脉冲多普勒(pulse Doppler, PD)雷达中的多普勒模糊问题，并且在检测目标的过程中比采用脉冲多普勒调制信号的计算量更小，性能更高。

近年来，Sen和Nehorai等人对OFDM雷达在城市环境下的运动目标检测性能做了分析，建立了采用OFDM波形的信号收发模型，并指出了其在检测概率上相对于LFM信号的优势[11]。此外，OFDM模糊函数、相关等信息可以用来进一步提高波形检测的精度[12]。现如今，OFDM波形的应用主要集中在地基雷达，但是，将该波形应用到机载雷达也是日后可能的发展方向。因此，本文将主要研究OFDM波形在机载雷达的应用，利用其对地面运动目标进行杂波抑制和检测分析，这也将成为雷达领域发展的不可替代的重要分支。

本文第2节介绍了基于OFDM波形的机载雷达运动目标检测的参数模型。第3节提出了一种具有假设条件的新型的广义似然比检验(generalized likelihood ratio, GLR)来对目标进行杂波抑制和目标检测，这个检验中使用了对目标信息的最大似然估计(maximum likelihood estimate, MLE)；另外，还采用了纽曼—皮尔逊(Neyman-Pearson, NP)准则来描述检测概率和虚警概率的关系。第4节给出了GLR检验的仿真结果和目标最小可检速度(minimum detection velocity, MDV)，测试了该检验的性能。

1 回波模型

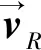
(1)

φt(t)=[ejω1Dt,ejω2Dt,…,ejωlDt,…,ejωLDt]T，

φc(t)=[ejωc1Dt,ejωc2Dt,…,ejωclDt,…,ejωcLDt]T

Φt=[φt(t1),φt(t2),…,φt(tN)]，

Φc=[φc(t1),φc(t2),…,φc(tN)]

φ表示导向矢量，Φ是其矩阵形式。ωlDt=2πβtfl和ωclDt=2πβcfl(fl表示第l个子载波频率)分别包含了目标和杂波的多普勒信息。这里“t”和“c”分别指代目标和杂波的参数。因此，总的L个子信道的输出可以写为

Y=AXtΦt+AXcΦc+E

(4)

其中

·A=diag{a1,a2,…,aL}是L×L的复对角的传输权重矩阵；

·Φc是L×L的导向矢量矩阵，它不是复高斯随机分布，但具有一个未知的协方差矩阵∑c；

E～δ·λ·NL,N(0,IN⊗σ2IL)，其中λ=20-(CNR/10)表示杂波噪声比(clutter-to-noise ratio, CNR)，单位为dB，IN,IL分别是N维和L维的单位矩阵，“⊗”表示Kronecker乘积，σ2是噪声的方差。

另外，需要指出的是，在机载雷达情况下XcΦc不服从复高斯随机分布，不能像地基静止雷达一样被认为是噪声。这是因为当机载雷达运动时，地面上的点杂波也会具有与运动目标同样的效果，其导向矢量Φc不再是一个单位矩阵。但是由于杂波的导向矢量已知，可以从式推出Φc，因此XcΦc仍然是已知的。

2 基于机载雷达的广义似然比检验

在本节中，将基于GLR检验[16]来进行杂波抑制和目标检测。GLR检验是一种用未知参数的最大似然估计代替未知参数本身的一种方法，这个方法将有效减少估计过程的计算量。

首先，设定两个判决假设：目标不存在假设H0和目标存在假设H1，表示为

(5)

所以，在这两个判决假设下回波反射系数的似然函数可以写为

(6)

其中，参数γ表示判决门限，并且

(7)

(8)

(9)

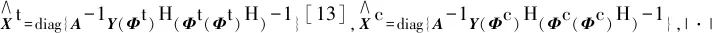
运动目标检测的性能可以通过纽曼—皮尔逊(Neyman-Pearson, NP)准则来进行分析。纽曼—皮尔逊准则是一种既不包含先验概率，也不需要估计代价的检测准则，其检测方法是在给定虚警概率(PFA)的条件下，使检测概率(PD)最大，这种方法在假设检验或信号检测中称为NP方法。对于一个给定的PFA=α，使PD最大的判决可以表示为(7)式，其中门限γ可以通过下式获得

(10)

根据文献[17]，可以得到

(11)

(12)

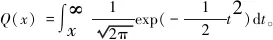
3 仿真实验及结果

本节采用MATLAB仿真软件对雷达场景进行了仿真，测试了GLR检验的性能，并对MDV进行了简要的分析。

3.1 杂波抑制与目标检测仿真

图1 运动雷达情况下不同TCR与GLR关系图

从图1中可以看出，即随着TCR增大，GLR不断降低，说明了此时目标回波与背景噪声的分离程度不断增强，也就是说杂波抑制的效果越来越好。随着TCR的进一步增大，GLR趋近于1，此时的杂波抑制接近于理想情形。

下面设γ∈[1,102]，CNR=5 dB，可以得到在不同的γ情况下虚警概率PFA和检测概率PD如图2所示。

图2 目标检测性能

从图2(a)可得，较高的TCR会带来更好的目标检测性能。尤其当TCR由5 dB上升至8 dB时，检测性能的提高较为明显。当约束PFA=10-3时，在三种TCR下的PD≈0.62,0.59,0.43，此时的雷达对目标的检测性能并不是很高。但如果改变约束条件，如约束PFA=0.1时，PD≈0.95,0.94,0.91，目标检测性能就得到了较大的提高，此时已经可以较好地完成目标检测任务。图2(b)保持TCR=10 dB，反映了OFDM信号频率的多样性可以提高检测性能。根据图中的结果，通过增加通道数可以有效提高目标检测性能。例如，在PFA=0.1时，5个子信道的OFDM系统PD≈0.65，而单个子信道仅有PD≈0.2。

3.2 目标最小可检速度

在对运动目标进行检测的过程中，另一个很重要的指标就是确定不同信杂比情况下的目标最小可检速度。最小可检速度，是指在不同的信杂比条件下，给定一个门限，使GLR能超过门限值的最小目标速度[18]。为与第4.1节保持一致，取γ=1(0 dB)，TCR=-10,-8,-5 dB，CNR=10 dB，可以得到MDV的信息如图3所示。

图3 目标最小可检速度信息

从图3(a)中可以看出，较高的TCR有利于获得更大的GLR，从而完成运动目标的检测。当TCR=-10,-8,-5 dB时，目标的最小可检速度的绝对值分别为±3.2 m/s, ±2.35 m/s, ±1 m/s，其中速度的正负号分别表示目标远离和相向雷达运动。由于当目标运动速度v=0时，目标不存在一个合理的GLR来检测，因此设定GLR的值为-∞。图3(b)显示MDV的绝对值随TCR的减小而增大。这是因为根据雷达检测原理，雷达是通过运动目标的多普勒频移来进行运动目标检测。当多普勒频移过小(小于杂波的多普勒频移)，或者说目标运动速度过低，那么它就不能与杂波区分开来。因此，我们只能通过增大TCR来获得运动目标的信息。

4 结 语

本文首先建立了基于OFDM波形的目标回波模型，然后采用GLR检验实现了杂波抑制和运动目标检测。尽管GLR检测不是最佳的，但是它的实际效果被证明很好。为了测试GLR检验的性能，本文仿真了目标的检测和虚警概率以及MDV，以说明其良好的性能。但是，本文只研究了匀速运动和传输权重为1的特殊情况，并且只是对单个目标进行的仿真。

在后续的工作中，作者将把模型扩展至非匀速运动时的情况，在设置目标回波和杂波的反射系数时，可以采用多维指数函数，将其它的各类影响因素也作为变量考虑进去。另外，还会增加杂波地物的数目，其位置的选取也更加随机，以全方位地对目标回波产生影响，将模型推广到更复杂的情况。