选取环路切换策略的高动态载波跟踪算法研究*

雷明东，杨守良，杨保亮，干红平

(重庆文理学院 电子电气学院，重庆 402160)

选取环路切换策略的高动态载波跟踪算法研究*

雷明东，杨守良，杨保亮，干红平

(重庆文理学院 电子电气学院，重庆 402160)

针对基于环路切换的传统GPS跟踪环路，会因为载体运动背景的复杂性而出现环路切换频繁，造成环路抖动和跟踪效果差的问题，提出了基于环路切换策略的高动态载波跟踪算法。该算法首先利用频率、相位判决器选择带有切换策略的子环路工作，然后利用切换策略模块去控制子环路对信号进行跟踪。仿真结果表明：载体在信号强度为45 dB·Hz，以5 g和10 g加速度分时间段做匀加速运动的场景下，基于环路切换策略的高动态载波跟踪算法能使得环路的切换次数和抖动现象明显减少，跟踪效果更佳。

全球定位系统；切换策略；高动态；判决器；跟踪；抖动

0 引言

近年来，随着卫星导航技术不断发展，国内外学者针对高动态GPS载波跟踪算法进行了大量的研究[1-2]。如Elliott D. Kaplan针对载波跟踪环分析了不同鉴相器和鉴频器的特点；Jwo D J利用载波跟踪环路误差与环路带宽的关系，分析了环路获得最佳带宽的方法[3]；Ward P W，Stefan K和Roncagliolo P A等人提出一种利用锁频环和锁相环相结合，同时工作的新型环路，使得该复合环路在动态适应性和精度方面达到了较好的平衡[4-6]；美国喷气推进实验室(JPL)的R.Kumar，S.Hinedi，W.J.Hurd等人针对无辅助的GPS高动态跟踪提出了多种算法，比如最大似然估计算法(MLE)、自动频率控制环(AFC)、扩展卡尔曼滤波器算法(EKF)等[7-8]。

本文主要针对传统跟踪环路方案在复杂的运动场景下，载波环路会在不同的子环路之间进行切换，造成跟踪环路抖动和跟踪精度降低的问题，本文在传统载波组合跟踪算法的基础上，提出适合于复杂运动背景下基于环路切换策略的高动态载波跟踪算法。

1 传统的载波组合跟踪算法

由于锁频环(FLL)能直接跟踪载波频率，环路鉴频器输出的鉴频误差值是输入信号和本地信号之间的载波频率误差，其具有更好的动态适应性和对复杂环境的适应性。相比较锁频环，锁相环(PLL)能直接跟踪输入信号的载波相位，环路鉴相器输出的值为输入信号和本地信号之间的载波相位差值；PLL一般适用于中低态的场景中，其跟踪精度明显高于FLL环路。而现实环境中，载体以较大多普勒和变多普勒运动的时间较短暂，而以变换缓慢的多普勒运动为主。所以许多学者[9-11]提出较理想的载波跟踪方案是：通过FLL和PLL交替工作来实现对信号的跟踪。在载体运动平缓时采用PLL来跟踪，此时环路带宽设计较窄以获取较高的精度；而载体运动剧烈时，环路切换到动态适应性好的FLL环，此时环路的带宽设置较宽。常见的载波跟踪算法如图1所示。

虽然传统的载波跟踪环路方案充分利用了PLL和FLL环的各自优点，实现了载波跟踪环路精度和动态性之间的最大平衡，然而由于载体运动背景的复杂性，会使得整个载波环路在子环路之间不间断进行切换，使得整个载波跟踪环路的跟踪产生一定的抖动，降低跟踪效果。

图1 传统载波跟踪环路算法框图Fig.1 Block diagram of traditional carrier tracking loop algorithm

2 基于环路切换策略的高动态载波跟踪算法

2.1 基于环路切换策略的高动态载波跟踪算法基本原理

本文所提出的基于环路切换策略的载波跟踪算法在传统算法的基础上，新增加一个环路切换策略模块，该环路模块通过动态检测各子环路的工作状态，使得环路从原来满足频率、相位条件后进行切换，转化为既要满足频率、相位切换条件，也需要满足环路的切换策略后才能进行环路之间的切换，该总体算法框图见图2。

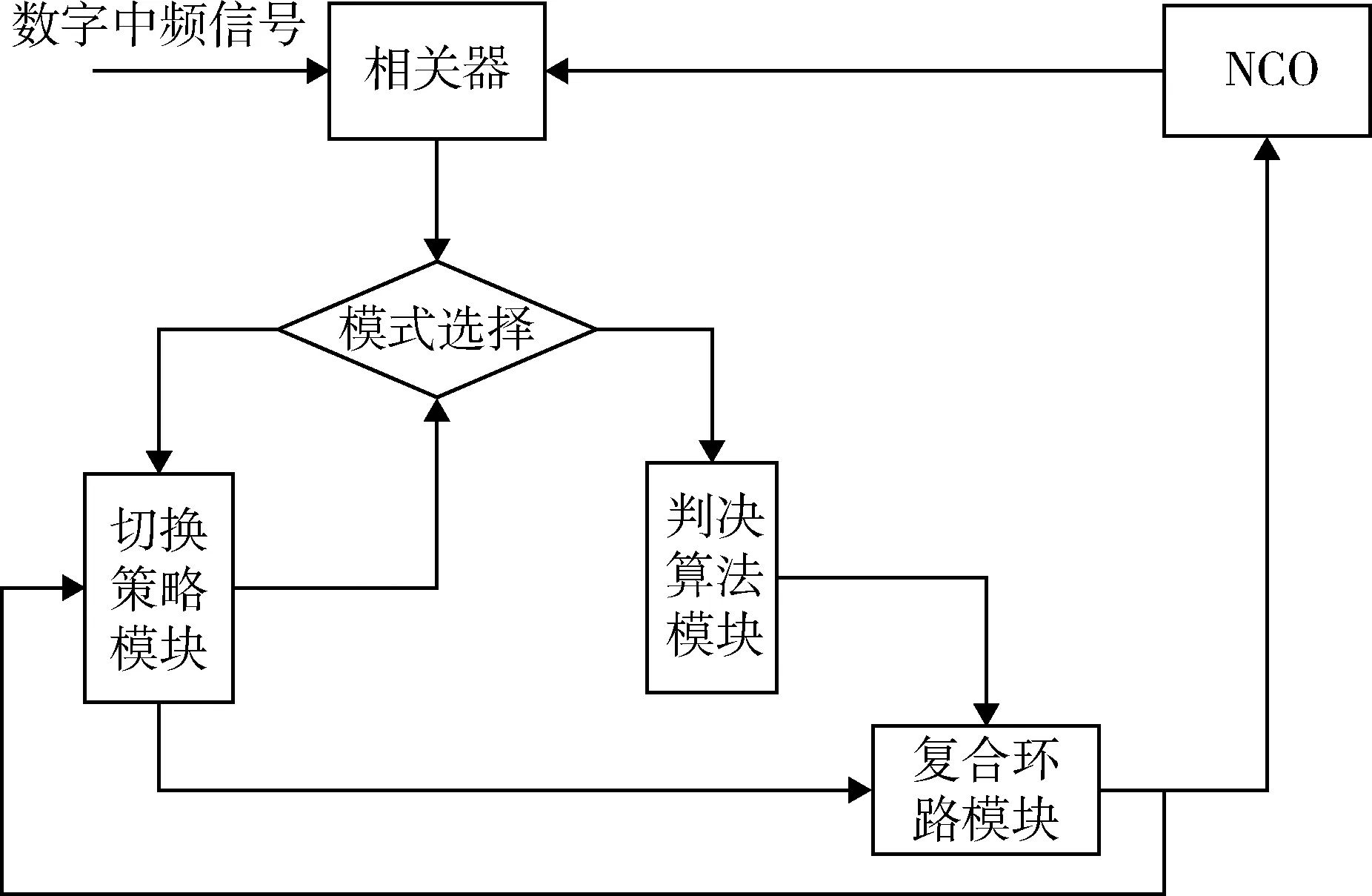
图2 基于环路切换策略的高动态载波跟踪算法原理框图Fig.2 Block diagram of high dynamic carrier tracking algorithm based on switching strategy

2.2 环路关键参数设计

2.2.1 判决算法模块

该模块是在对信号捕获完成后，跟踪环路初始进入工作跟踪状态时，用于选择跟踪子环路的判决算法。本算法主要涉及相位判决算法、频率判决算法的设计，以及相位和频率门限值的选取。

(1) 相位判决算法

相位门限值判决公式为

(1)

Ip(k)和Qp(k)2路信号模型的表达式为

Ip(k)=0.5AD(k)R(ε(k))·

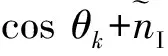
(2)

Qp(k)=0.5AD(k)R(ε(k))·

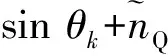
(3)

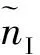
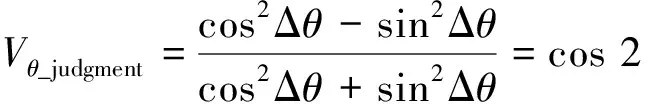
(4)

式中：Δθ为残余载波相位。 因此，对一般高动态条件下，在忽略弱信号影响的情况下，通过测量Vθ_judgment的值，能粗略的反应Δθ值的大小，从而为环路的切换提供判决信息。

(2) 频率判决算法

频率门限值的判决公式如下[12-13]：

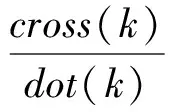
Δfd=Δf，

(5)

式中：

cross(k)=I(k)Q(k-1)-Q(k)I(k-1)=

Asin(2πΔfdNTs),

(6)

dot(k)=I(k)I(k-1)+Q(k)Q(k-1)=

Acos(2πΔfdNTs).

(7)

通过测量Vf_judgment的值，能够粗略地反映出环路的多普勒频率残余差值，从而为环路提供相应的判决信息。

通过上述算法研究，判决算法模块的原理图参见图6。

(3) 判决算法门限值的确定[14]

判决算法门限值的确定是根据Monte Carlo模拟所确定的，对于图2子环路loop2，loop3中的锁相环，其环路相位误差Δθ必须小于式子(8)～(10)所确定的门限值，环路才能正常工作。而在确定本文运动参数情况下，Δθ的可取值范围如图3(黑色线表示其取值上限)所示。考虑锁相环路的快速收敛区间较小，所以本文中相位的切换门限Δθ取值为10°。

3Δθ=3σtPLL+θePLL≤45°,

(8)

(9)

(10)

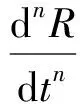
图3 3阶PLL环路取值门限Fig.3 Threshold value of 3 order PLL loop

与锁相环相似，对于锁频环，对于图2子环路loop1，loop2中的锁频环，其环路正常工作频率误差Δf必须小于由式子(11)～(13)所确立的取值门限，Δf取值范围如图4(黑色线表示其取值上限)：

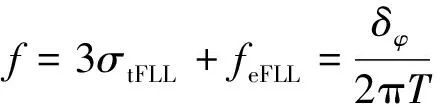
(11)

(12)

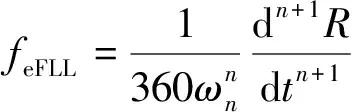
(13)

式中：3σtFLL为FLL热噪声频率颤动；feFLL为FLL环的动态应力误差。

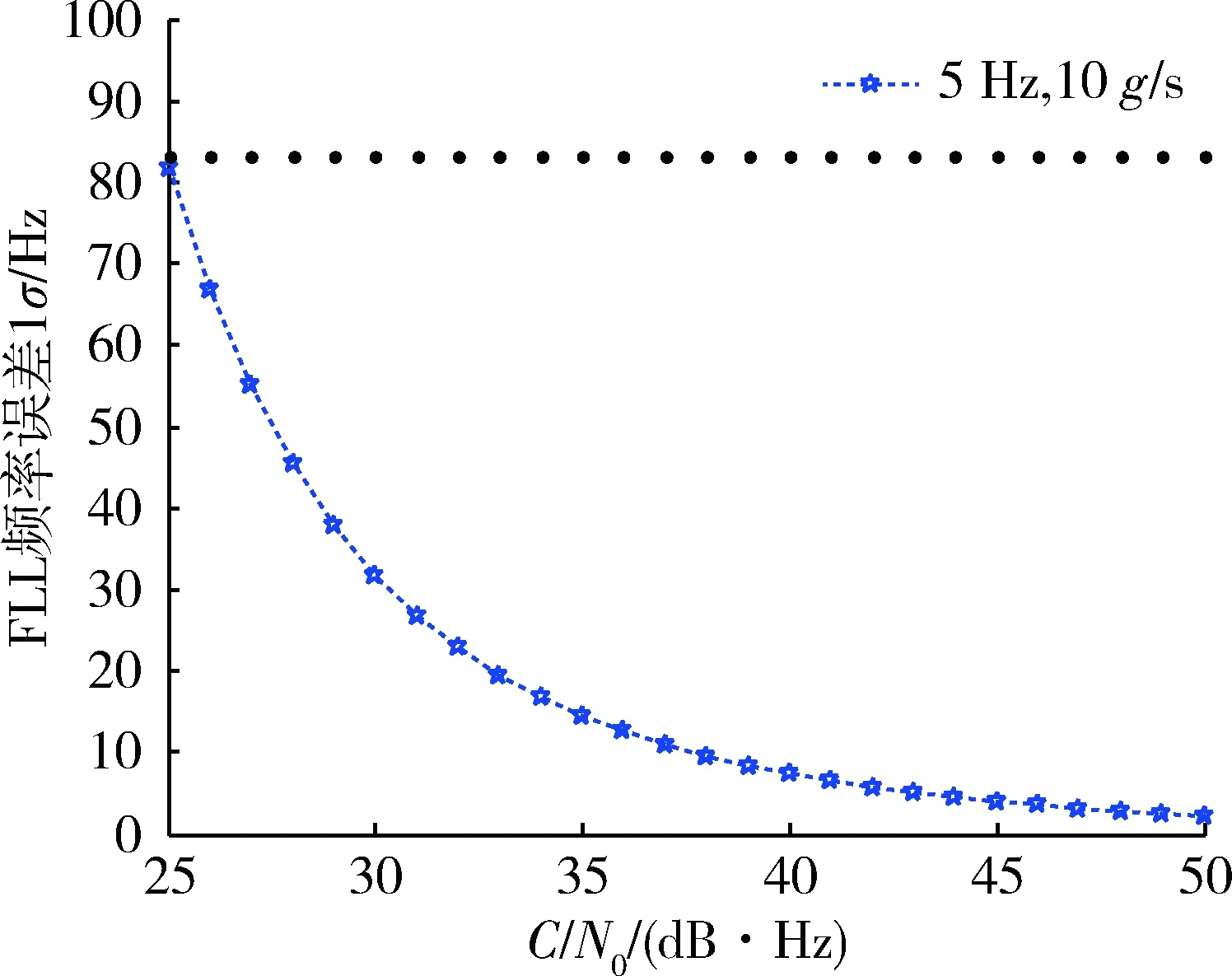
图4 2阶FLL环路取值门限Fig.4 Threshold value of 2 order FLL loop

本文T取值1 ms的情况下，为使得频差能快速进入锁相环工作频带，频率切换门限值Δf取值为30 Hz。

2.2.2 复合环路模块

在高动态场景中，为了使得接收机能迅速的捕获目标，捕获算法中预检积分时间一般取1 ms，即图5中频率搜索单元取值为666.67 Hz，即捕获后的最大多普勒频差将达到333.33 Hz，由于频差较大，这将远远超出锁相环的线性工作范围。为了解决该问题，当频率判决Δf≥30 Hz时，载波跟踪环路工作在含线性工作范围大的四象限反正切鉴频器的[14]子环路loop1，直到将捕获后的输入信号和本地信号之间的频差牵引到几十Hz，使得该频差能进入其他环路的工作范围内。为了加快频率牵引的速度，简化环路的计算量，在该子环路中没有使用滤波器，所以环路跟踪的精度不高，受噪声的影响较大。

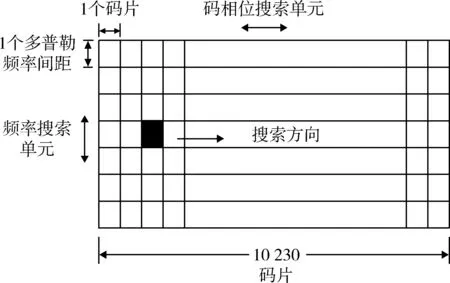
图5 捕获的二维空间搜索过程Fig.5 Captured two dimensional spatial search process

而当频率判决和相位判决满足Δf<30 Hz，Δθ≥10°时，载波跟踪环路工作在子环路loop2。在子环路loop2中，传统的跟踪环路一般直接采用FLL环路来适应载体大的动态。然而要从该环路跟踪的结果中获得导航电文，还需要对结果值进行相位旋转。而在本文中，为了能使得载波环路能在较大的动态条件下工作，子环路loop2采用2阶FLL辅助3阶PLL的复合环路[14-15]模式，由于该环路较好的兼顾了FLL和PLL环路的特点，使得该复合环路既可以设计较大的环路带宽来适应动态性，也可以从跟踪到的结果中直接获取导航电文而不用相位旋转。在该复合环路中鉴频器采用运算量小而线性工作范围适中的叉积鉴频器[14]；而鉴相器选择在不同信噪比下都具有最佳性能的二象限反正切鉴相器[14]。

由于2阶FLL辅助3阶PLL的复合环路，其跟踪精度会略低于纯3阶PLL环路，所以在载体的运动状态较平缓的时候，环路可以从复合环路转入纯锁相环路工作。因此，当频率判决和相位判决满足Δf<30 Hz，Δθ<10°时，载波跟踪环路进入子环路loop3。由于此时载体的运动较缓慢，所以子环路loop3可以设计较窄的环路带宽，以此获得较好的跟踪精度。而环路鉴相器的选择可以根据实际的仿真场景来进行选择。

通过上述算法研究，所选取的子环路组成的复合环路的原理框图参见图6。

2.3 环路切换策略模块

在各子环路中，添加切换策略模块的目的就是为了应对在复杂情况下环路频繁切换的问题，以此减小环路由抖动造成的跟踪精度损失。环路的切换策略的算法具体体现为：在子环路loopA(其中A=1，2，3)工作M次中，其中N次满足本环路的切换条件(M≥N)，并且在最后一次也满足本环路切换条件的情况下，根据频率、相位判决来设置环路切换变量loop的值，以此值来选择载波环路工作在第几子环路。

根据子环路的不同作用，其中M和N值的选择也不相同，为了将频差拉到门限以下，有效地防止抖动，loop1和loop2中M选择为10，N选择为8。而loop3主要工作在载体运动平缓的场景下，为了保证跟踪精度，环路的带宽设置较窄，所以为了保证整个载波跟踪环路更好的适应动态性，载波环路工作在loop3的时候，遇到较大动态时，能及时的从loop3快速切换到其他子环路，所以M选择为1，N选择为1。

通过上述算法研究，切换策略模块原理框图参见图6。

经过对图2中各个模块的分析，基于环路切换策略的高动态载波跟踪算法的具体原理框图如图6所示。

图6 基于环路切换策略的高动态载波跟踪算法原理框图Fig.6 Block diagram of high dynamic carrier tracking algorithm based on switching strategy

3 仿真实验及分析

本文采用基于Matlab版的软件接收机为测试平台，所使用的信号由GPS软件模拟器产生，本文中信号强度设置为45 dB·Hz，载体以静止状态运动2 s后，转入以5g加速度运动4 s，最后以10g的加速度做匀加速运动。载体的运动场景设置如图7所示。

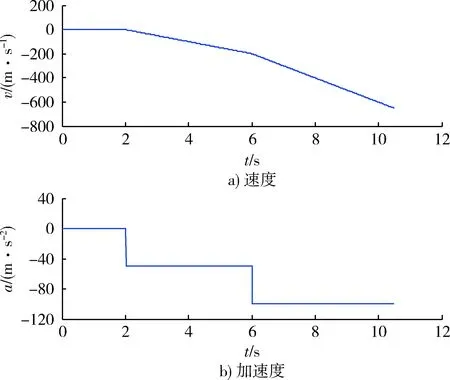
图7 载体运动的场景图Fig.7 Scene diagram of carrier motion

在实验中，将不加环路切换策略的传统载波跟踪环路方案和基于环路切换策略的载波跟踪环路方案对该仿真信号进行跟踪，其结果如图8～11所示。

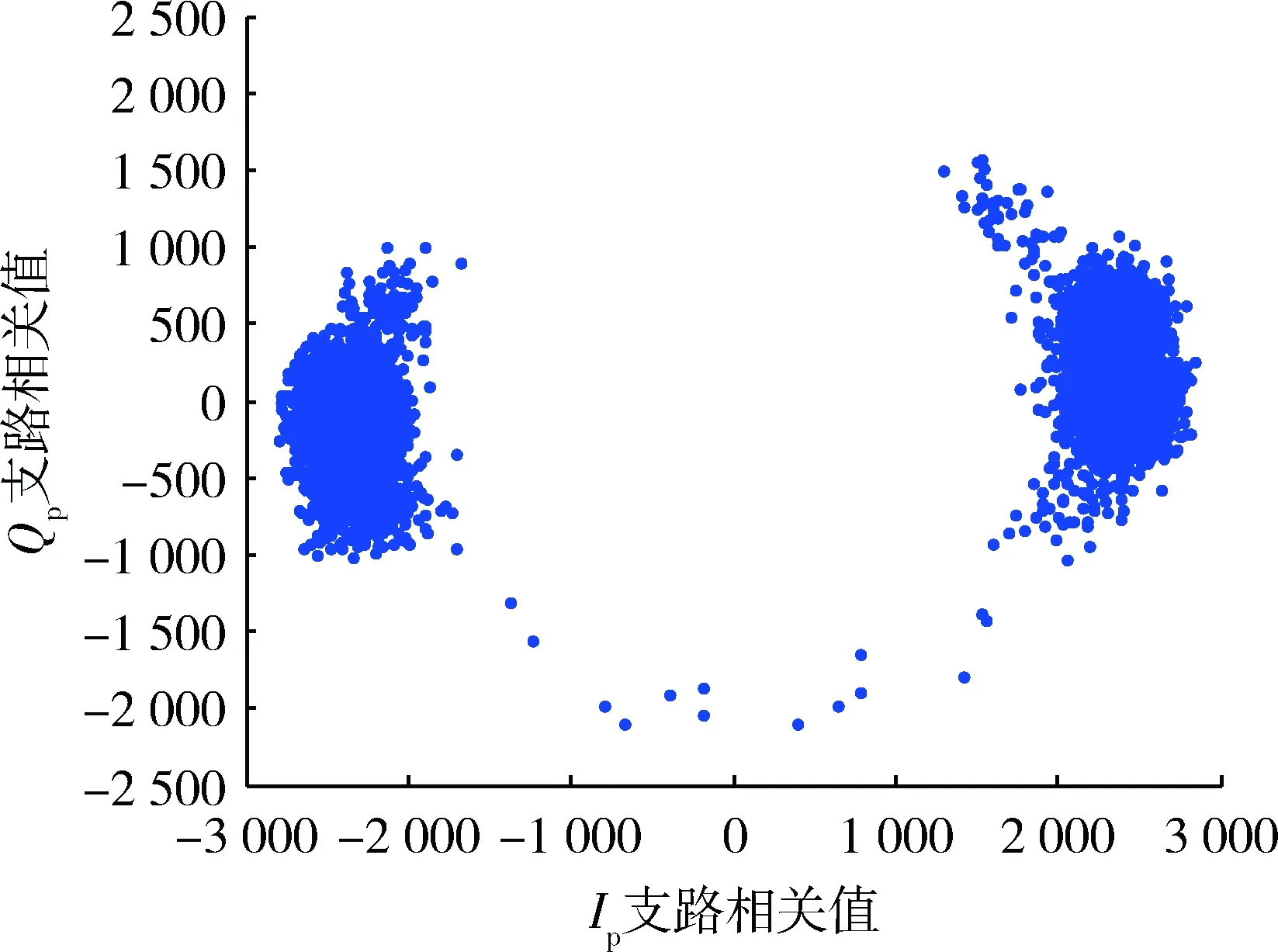
图8 传统载波跟踪环路输出Ip/Qp二维离散图Fig.8 Traditional carrier tracking loop output of Ip/Qpbranch discrete figure

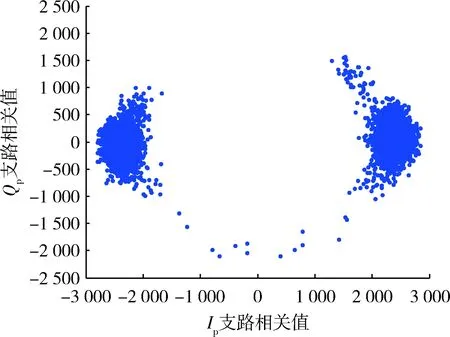
图9 带切换策略的载波跟踪环路输出Ip/Qp二维离散图Fig.9 Output of Ip/Qp branch with switching strategy of carrier tracking loop discrete figure

从图8,9的对比可以发现，传统载波跟踪环路输出的Ip/Qp二维离散图相比较带切换策略的载波跟踪环路输出的离散图分散，其中Qp值主要集中于±1 000之间，而后者的Qp值主要集中于±500之间。这说明传统载波跟踪环路在复杂运动场景下工作，环路切换次数增多，使得Qp输出值中还含有大量的信号能量，这也说明了其跟踪性能要弱于带切换策略的载波跟踪环路。

图10 传统载波跟踪环路中Ip/Qp输出值Fig.10 Traditional carrier tracking loop output value of Ip/Qp

图11 带切换策略的载波跟踪环路Ip/Qp输出值Fig.11 Output value of Ip/Qp with switching strategy of carrier tracking loop

表1 载波跟踪环路在各子环路之间切换次数的统计表

Table 1 Carrier tracking loop switching frequency statistics between each loop

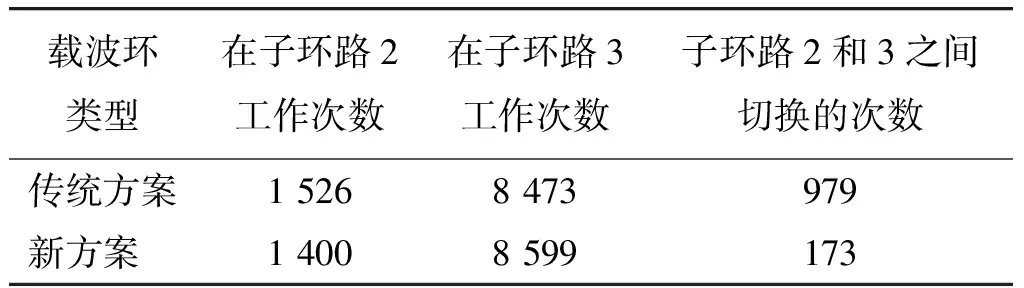
载波环类型在子环路2工作次数在子环路3工作次数子环路2和3之间切换的次数传统方案15268473979新方案 14008599173

而从表1来看，基于传统载波跟踪的环路在子环路2和3之间切换的频率比较高，在载波环路工作的10 s时间内，传统方案总共切换了979次，而新方案切换了173次，在加了切换策略后，使得载波环路的切换频次减少了82%；而新方案中，载波跟踪环路工作在子环路3中的次数大于传统方案，由于子环路3采用的是单锁相环，所以其跟踪精度要高于子环路2中的复合环，这也会使得环路最终的跟踪效果要好于传统的载波跟踪环路。

从图10，11和表1中2种载波跟踪环路输出的Ip和Qp值可以看出，在载波环路工作的初始阶段和载体动态变化的位置，载波环路的跟踪误差都会加大，使得Qp路信号的增加，导致跟踪精度的降低。而环路切换的越频繁，整个载波环路的抖动现象越严重，跟踪的效果越差。因此从上述实验结果中可以得出：基于环路切换策略的载波跟踪环路方案，使得环路的切换次数减少，环路抖动减小，环路的跟踪效果更佳。

4 结束语

本文首先概述了应用在高动态环境下的传统载波跟踪环路算法，该算法充分利用了FLL环路动态适应性好、PLL环路跟踪精度高的特点，使得载波环路在跟踪精度和动态性两者之间达到了较好的平衡。针对于该算法会因为载体运动背景的复杂性而出现环路切换频繁，造成环路的抖动和跟踪效果降低的问题，本文提出了基于环路切换策略的载波跟踪环路算法。文中详细分析了新算法中涉及的载波子环路和环路切换策略，并给出了参数的具体取值。仿真表明：载体在信号强度为45 dB·Hz，以5g和10g加速度分时间段作匀加速运动的场景下，基于环路切换策略的高动态载波跟踪算法使得环路的切换次数和抖动现象明显减少，跟踪效果更佳。

[1] 向洋.高动态GPS载波跟踪技术研究[D].武汉：华中科技大学，2010. XIANG Yang. Study on High Dynamic GPS Carrier Tracking Technigues[D].Wuhan：Huazhong University of Science and Technology，2010.

[2] 张晶泊.GNSS软件接收机高动态载波跟踪环路关键技术研究[D].大连：大连海事大学,2012. ZHANG Jing-bo.The Key Technologies of the High-Dynamic Carrier Tracking Loop in GNSS Software Receiver[D].Dalian：Dalian Maritime University,2012.

[3] JWO D J. Optimisation and Sensitivity Analysis of GPS Receiver Tracking Loops in Dynamic Environments [J]. IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(4): 241-250.

[4] WARD P W. Performance Comparisons Between FLL, PLL and a Novel FLL-Assisted-PLL Carrier Tracking Loop under RF Interference Conditions [C]∥Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1998)，1998: 783-795.

[5] STEFAN K, CHRISTIAN A, DANIEL G, et al. GNSS Receiver with Vector Based FLL-Assisted PLL Carrier Tracking Loop [C]∥ION GNSS 21st International Technical Meeting of the Satellite Division. Savannah CA: The Institute of Navigation, 2008: 197-203.

[6] RONCAGLIOLO P A, GARCIA J G. High Dynamics and False Lock Resistant GNSS Carrier Tracking Loops[C]∥Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007)，2001: 2364-2375.

[7] 王伟，张廷新，史平彦.高动态环境下GPS信号跟踪算法综述[J].空间电子技术，2000(1)：1-9. WANG Wei, ZHANG Ting-xin, SHI Ping-yan. GPS Signal Tracking Algorithm Survey Under High Dynamic Environment [J]. Space Electronic Technology，2000(1)：1-9.

[8] HINEDI S, STATMAN J I. High-Dynamic GPS Tracking Final Report[R]. JPL Publication 88-35, 1988, 12: 1-84.

[9] 田明坤,邵定蓉.高动态GPS接收机的一种设计方案[J]. 遥测遥控, 2002, 23(3)：15-20. TIAN Ming-kun,SHAO Ding-rong. One Design of High Dynamic GPS Receivers[J]. Journal of Telemetry,Tracking and Command, 2002, 23(3)：15-20.

[10] 邓晓武，孙武.基于FLL+PLL的载波跟踪环路设计[J].现代防御技术，2010,38(4)：137-141. DENG Xiao-wu, SUN Wu. Design of Carrier Tracking Loop Based on FLL+PLL [J]. Modern Defence Technology，2010,38(4)：137-141.

[11] 王仕成,杨东方,刘志国,等.一种高动态GPS软件接收机方案研究[J].宇航学报, 2009, 30(3): 1079-1085. WANG Shi-cheng, YANG Dong-fang, LIU Zhi-guo,et al. A Highly Dynamic Software GPS Receiver Scheme[J]. Journal of Astronautics, 2009, 30(3): 1079-1085.

[12] 胡辉，雷明东，李林，等.高动态GPS载波跟踪组合环路控制策略[J]. 探测与控制学报，2014，36(1):11-16. HU Hui,LEI Ming-dong,LI Lin,et al. A Control Strategies of Combination of GPS Carrier Tracking Loop Under High Dynamic[J].Journal of Detection & Control, 2014，36(1):11-16.

[13] 胡辉，雷明东，杨保亮，等. 利用查找表的动态载波环路增益控制算法[J].河南科技大学学报：自然科学版，2015，36(2):49-52. HU Hui, LEI Ming-dong, YANG Bao-liang, et al. The Dynamic Carrier Loop Gain Control Algorithm with the Look-up Table [J]. Journal of Henan University of Science and Technology: Natural Science ed，2015，36(2):49-52.

[14] KAPLAN E D, HEGARTY C. Understanding GPS: Principles and Applications[M]. 2nd ed. USA:Artech House Publishers, 2005.

[15] 郝学坤, 马文峰, 方华, 等. 三阶锁相环跟踪卫星多普勒频偏的仿真研究[J]. 系统仿真学报, 2004, 16(4): 625-627. HAO Xue-kun, MA Wen-feng, FANG Hua,et al. The Study of Simulation for Tracing Satellite Doppler Shift Using Third-Order Phase-Locked loop[J]. Journal of System Simulation, 2004, 16(4): 625-627.

High Dynamic Carrier Tracking Algorithm of Choosing Loop Switching Strategy

LEI Ming-dong, YANG Shou-liang, YANG Bao-liang, GAN Hong-ping

(Chongqing University of Arts and Science, College of Electrical and Electronic, Chongqing 402160, China)

Traditional GPS tracking is based on the loop switching. Because of the complexity of carrier motion background, the loop switching is frequent, resulting in the problem of loop jitter and poor trackin. To solve this problem, a high dynamic carrier tracking algorithm based on switching strategy is proposed . In this algorithm, the frequency and the phase decision devices are used to select the sub loop with the switching strategy. Then, the switching strategy module is used to control the sub loop to track the signal. The simulation results show: when the carrier signal strength is 45 dB·Hz and a uniformly accelerated motion scene is 5gand 10gof acceleration in different time intervals, the high dynamic carrier tracking algorithm based on switching strategy can significantly reduce the number of switching and jitter of the loop, and a better tracking results is obtained.

global positioning system(GPS); switching strategy; high dynamic; decider; tracking; jitter

2016-04-07；

2016-06-06 基金项目：重庆市教委科技项目(KJ131208)；重庆文理学院校级科研项目(Y2014DQ31) 作者简介：雷明东(1987-)，男，重庆永川人。助教，硕士，主要研究方向为信号与信息处理，卫星导航定位。

10.3969/j.issn.1009-086x.2017.02.022

TN967.1；TP301.6；TP391.9

A

1009-086X(2017)-02-0142-07

通信地址：402160 重庆市永川区红河大道319号 E-mail：leimingdongok@163.com