由椭圆张角为直角的弦所在直线形成的“包络”
2019-12-16广东省中山纪念中学528454李文东
广东省中山纪念中学(528454) 李文东
一族平面直线(或曲线)的“包络”是指一条与这族直线(或曲线)中任意一条都相切的曲线,这条曲线叫做这族直线(或曲线)的包络线.文[1]中探讨了由椭圆=1(a>b>0)内对称轴上一点P引两垂直直线PA,PB分别交椭圆于点A,B,得到了动直线AB形成的包络曲线方程,并且对于椭圆内任意一点P(x0,y0)(原点除外)的包络线情形给出了一个猜想:
包络线是以P(x0,y0)和为焦点,长轴长为的椭圆,但是没有给出证明和具体的包络线方程.
本文对于上述结论给出证明并将此结论推广到点P(x0,y0)为平面内任意满足条件PA⊥PB的情形,其推导和证明过程如下:
一、运用齐次化手段推导动直线满足的条件
二、利用对称点推导动直线的包络线
首先给出如下引理:
引理设圆M的半径为r,点A为圆M上一动点,点N为不在圆M上一定点,线段AN的垂直平分线为l,l交MA(或其延长线)于点P,则
(1)当点N为圆M内一定点时,垂直平分线l的包络线即点P的轨迹是以点M,N为焦点,长轴长为r的椭圆;
(2)当点N为M外一定点时,垂直平分线l的包络线即点P的轨迹是以点M,N为焦点,长轴长为r的双曲线.
证明以椭圆为例.如图1,由题意:|PA|=|PN|,故|PM|+|PN|=|PA|+|PM|=|AM|=r>|MN|,由椭圆的定义知:点P的轨迹是以点M,N为焦点,长轴长为r的椭圆.
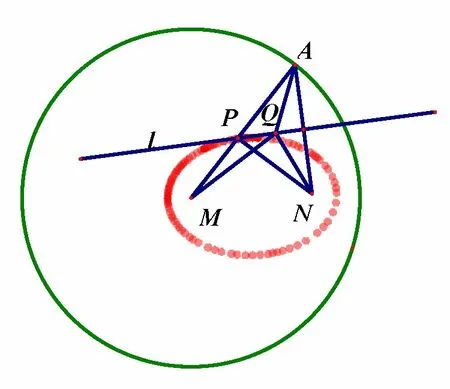
图1
以下证明直线l与椭圆相切.设点Q为直线l上异于点P的任意一点,则|QM|+QN|=|QA|+|QM|>|AM|=|PM|+|PN,即点Q在椭圆外,故点P为直线l与椭圆的唯一公共点,即直线l与椭圆相切于点P.证毕.
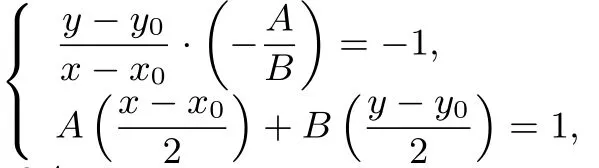
(1)若m = 0,即点P(x0,y0)为椭圆上一点,则2b2x0A+2a2y0B+a2+b2=0,即Ax0+=Ax0+By0+1,而直线AB的方程为Ax+By=Ax0+By0+1,联立可得:By0=Ax+By,即可见此时直线AB过定点
(i)若点P(x0,y0)为椭圆=1(a>b>0)内除原点外任意一点,即且则
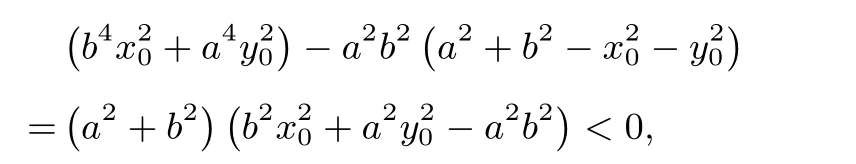
从而
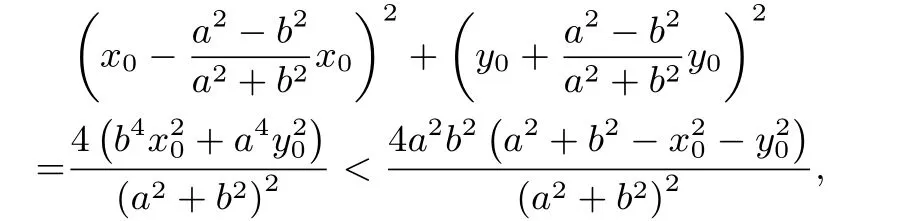
即点P(x0,y0)在Q(x,y)的轨迹方程圆内,从而由引理可知,MQ与直线AB的交点,即直线AB的包络线是以和P(x0,y0)为焦点,长轴长为的椭圆(如图2);
(ii)若点P(x0,y0)在椭圆=1(a>b>0)外,且满足>0,即点P(x0,y0)在椭圆的蒙日圆x2+y2=a2+b2内,由引理可知此时直线AB的包络线是以和P(x0,y0)为焦点,实轴长为的双曲线(如图2).
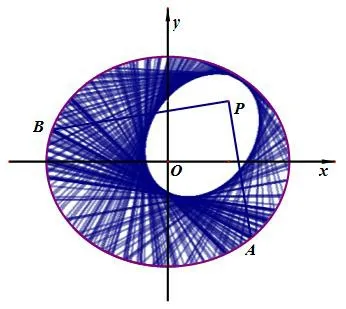
图2

图3
(iii)若P为原点,即x0=y0=0,此时包络线为一个圆,其方程为:
三、包络线的统一方程
根据第二部分的推导,根据圆锥曲线的定义,我们可以得到包络线的统一方程为:()x2+-2a2b2x0y0xy-2a2b2x0(t-b2)x-2a2b2y0(t-a2)y-=0.其中
限于篇幅,具体推导过程留给感兴趣的读者!
