椭圆与两焦点弦有关的几个重要性质及其推论

山东省邹平双语学校(256200) 姜坤崇

我们把过圆锥曲线焦点的弦称为它的焦点弦,焦点弦是圆锥曲线中的重要线段,许多性质都与它有关. 本文给出椭圆与两条满足一定条件的焦点弦有关的几个重要性质及其推论. 由于椭圆具有轴对称性,因此以下对于只涉及一个焦点的结论,不失一般性,我们均设焦点弦为左焦点弦.

定理1给定椭圆E:= 1(a ＞b ＞0),AB、CD是过E左焦点F1(-c,0)(c=以下同)的两条互相垂直的弦,则为定值

证明(1) 如图1, 当AB不为E的长轴和垂径(过焦点且垂直于焦点轴的弦) 时,CD亦不为E的长轴和垂径,设A(x1,y1),B(x2,y2),直线AB、CD的斜率分别为k1、k2, 则直线AB、CD的方程分别为y=k1(x+c)、y=k2(x+c), 将y=k1(x+c) 代入E的方程整理得(a2k21+b2)x2+2a2ck21x+a2(c2k21-b2)=0.

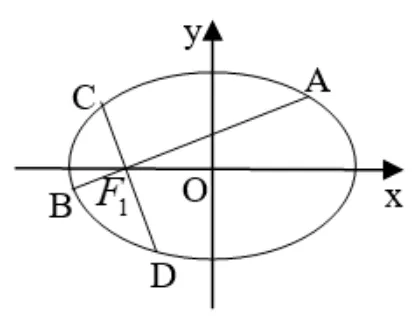
图1

由于x1,x2为以上关于x的二次方程的两个根,故由韦达定理得x1+x2=所以,

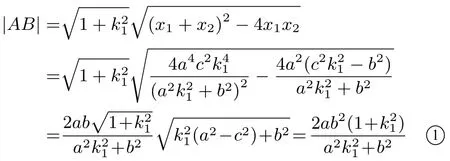
同理,

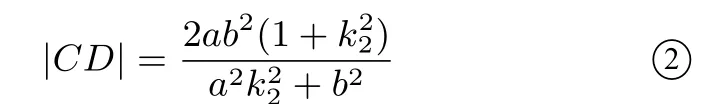
由于AB⊥CD,故k1k2=-1(k1k2/= 0),从而k21k22=1,于是

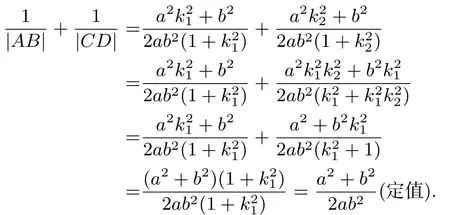
(2)当AB为E的长轴(垂径)且CD为E的垂径(长轴)时,不难验证亦成立,从略.

综合(1)、(2),定理1 得证.

推论1如图2,给定椭圆=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦点,AB、CD分别是E过F1、F2且互相垂直的弦,则为定值

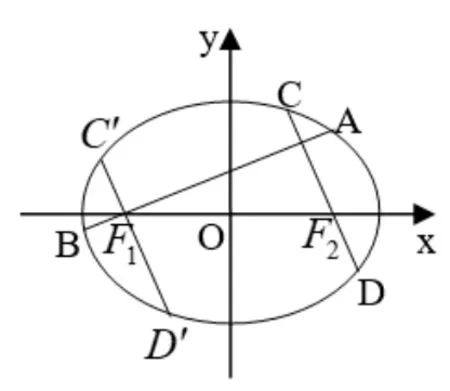
图2

证明过F1作与CD平行的弦C′D′,则由椭圆的中心对称性知|C′D′|=|CD|,又由AB⊥CD得AB⊥C′D′,于是由定理1 的结论知

推论2如图3,给定椭圆E:=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦点,P是以F1F2为直径的圆E1:x2+y2=a2-b2上异于F1、F2的任一点,直线PF1和PF2与E的交点分别为A、B和C、D,则为定值

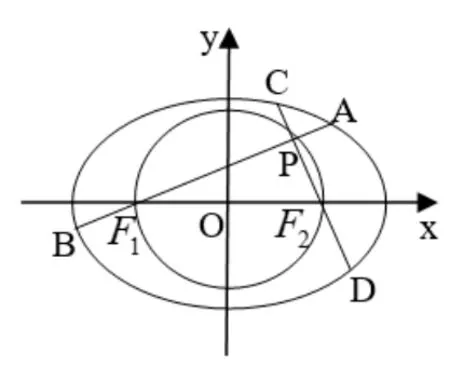
图3

证明由F1F2为E1的直径知PF1⊥PF2,于是由定理1 推论1 的结论可得

推论3如图4,给定椭圆E:=1(a ＞b ＞0),AB、CD是E的过左焦点F1(-c,0)的两条弦,kAB·kCD=1(kAB、kCD分别为直线AB、CD的斜率,以下同)或AB、CD分别为E的长轴与垂径, 则为定值

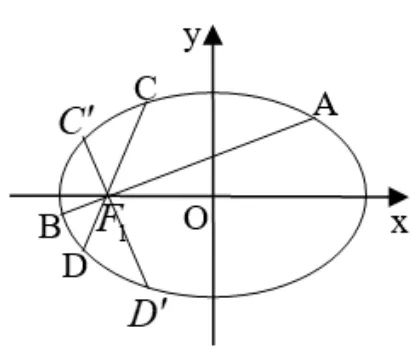
图4

证明当AB、CD有一条与x轴垂直(即AB、CD分别为E的长轴与垂径) 时, 由定理1 知结论成立; 当AB、CD均不与x轴垂直时,作弦CD关于x轴的对称弦C′D′,则由椭圆的轴对称性知|C′D′|=|CD|,kCD=-kC′D′,kAB·kC′D′=-kAB·kCD=-1,从而AB⊥C′D′,于是由定理1 的结论知

推论4如图5,给定椭圆=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦点,AB、CD分别是E过F1、F2的弦,kAB ·kCD=1 或AB、CD分别为E的长轴与垂径,则为定值

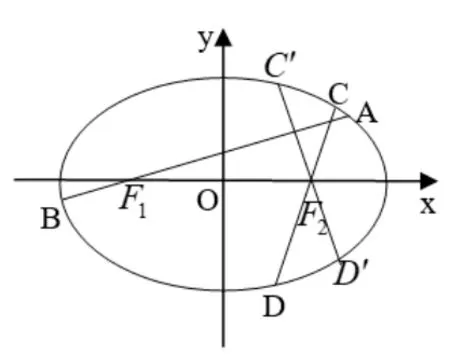
图5

证明当AB、CD有一条与x轴垂直(即AB、CD分别为E的长轴与垂径) 时, 由定理1 知结论成立; 当AB、CD均不与x轴垂直时,作弦CD关于x轴的对称弦C′D′,则由椭圆的轴对称性知|C′D′|=|CD|,kCD=-kC′D′,kAB ·kC′D′=-kAB ·kCD=-1,从而AB⊥C′D′,于是由定理1 推论1 的结论知

推论5如图6,给定椭圆=1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦点,P是以F1、F2为两顶点的等轴双曲线E1:x2-y2=a2-b2上异于F1、F2的任一点, 直线PF1和PF2与E的交点分别为A、B和C、D,则

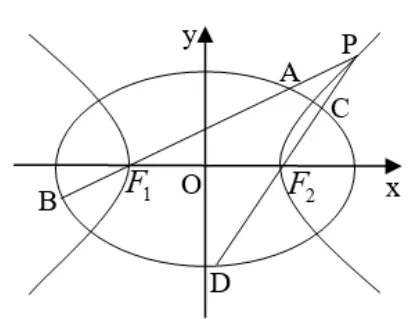
图6

证明设P(x0,y0), 则由点P在E1上知x20- y20=a2-b2,即y20=x20-a2+b2,于是

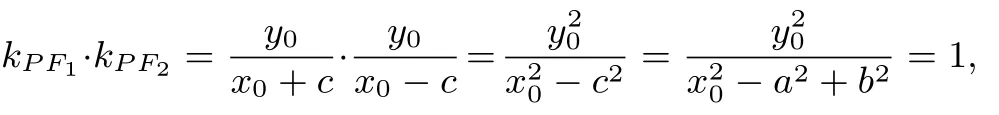
说明以上由定理1 证明5 个推论所用的方法同样适合于由下面的两个定理证明其相应的推论,因此限于篇幅以下各定理的推论的证明均不再给出.

定理2给定椭圆= 1(a ＞b ＞0),AB、CD是E的过焦点F1(-c,0)的两条弦,kAB ·kCD=或AB、CD分别为E的长轴与垂径,则|AB|·|CD|为定值4b2.

证明(1)如图7,当AB不为E的长轴和垂径时,CD亦不为E的长轴和垂径,设A(x1,y1),B(x2,y2),kAB=k1,kCD=k2,则直线AB、CD的方程分别为y=k1(x+c)、y=k2(x+c), 同定理1 的证明一样得到①、②式. 因为k1k2=所以于是

图7

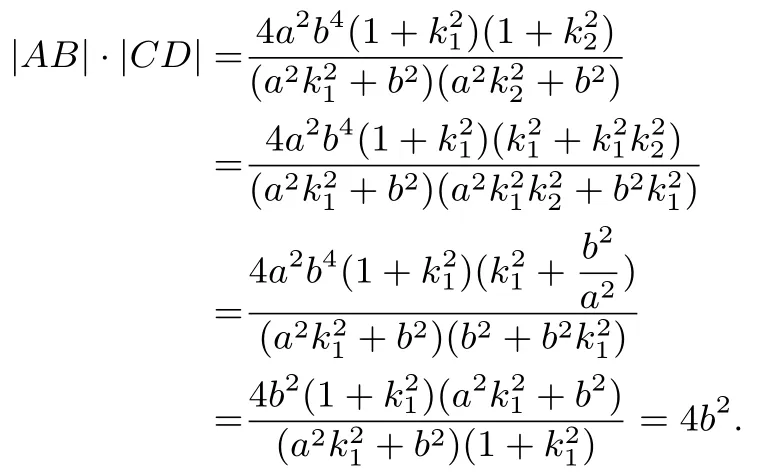
(2)当AB为E的长轴(垂径)且CD为E的垂径(长轴)时,不难验证|AB|·|CD|=4b2亦成立,从略.

综合(1)、(2),定理2 得证.

推论1给定椭圆E:= 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦点,AB、CD分别是E过F1、F2的弦,kAB·kCD=或AB、CD分别为E的长轴与垂径,则|AB|·|CD|为定值4b2.

推论2给定椭圆E:= 1(a ＞b ＞0),P是以E的两个焦点F1、F2为顶点且离心率为的椭圆= 1(其中c2=a2-b2)上异于顶点的任一点,直线PF1和PF2与E的交点分别为A、B和C、D,则|AB|·|CD|为定值4b2.

推论3给定椭圆E:= 1(a ＞b ＞0),AB、CD是E的过焦点F1(-c,0)的两条弦,kAB ·kCD=或AB、CD分别为E的长轴与垂径, 则|AB|·|CD|为定值4b2.

推论4给定椭圆E:= 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E的左、右焦点,AB、CD分别是E过F1、F2的弦,kAB·kCD=或AB、CD分别为E的长轴与垂径,则|AB|·|CD|为定值4b2.

推论5给定椭圆E:= 1(a ＞b ＞0),P是以E的两个焦点F1、F2为顶点且离心率为的双曲线=1(其中c2=a2-b2)上异于顶点的任一点,直线PF1和PF2与E的交点分别为A、B和C、D,则|AB|·|CD|为定值4b2.

定理3给定椭圆E := 1(a ＞b ＞0),AB、CD 是E 的过焦点F1(-c,0)的两条弦,kAB·kCD=或AB、CD 分别为E 的长轴与垂径,则|AB|+|CD|为定值

证明(1) 如图8, 当AB不为E 的长轴和垂径时,CD亦不为E 的长轴和垂径, 设A(x1,y1),B(x2,y2),kAB=k1,kCD= k2, 则直线AB、CD 的方程分别为y =k1(x + c)、y = k2(x + c), 同定理1 的证明一样得到①、②式.

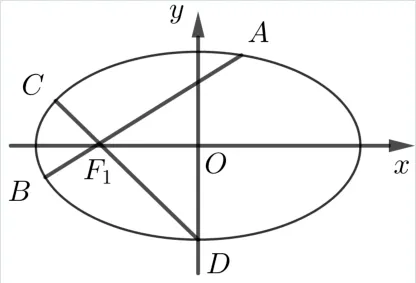
图8

因为k1k2=(k1k2/=0),所以k21k22=于是

(2)当AB 为E 的长轴(垂径)时,CD 为E 的垂径(长轴),不难验证|AB|+|CD|=亦成立,从略.

综合(1)和(2),定理3 得证.

推论1给定椭圆= 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E 的左、右焦点,AB、CD 是E 的分别过F1、F2的弦,kAB·kCD=或AB、CD 分别为E 的长轴与垂径,则|AB|+|CD|为定值

推论2给定椭圆E :=1(a ＞b ＞0),P 是以E 的两焦点F1、F2为长轴的两端点且与E 同离心率的椭圆E1:=1(其中c2=a2-b2)上异于F1、F2的任一点,直线PF1和PF2与E 的交点分别为A、B 和C、D,则|AB|+|CD|为定值

推论3给定椭圆E := 1(a ＞b ＞0),AB、CD 是E 的过焦点F1(-c,0)的两条弦,kAB·kCD=或AB、CD 分别为E 的长轴与垂径,则|AB|+|CD|为定值

推论4给定椭圆E := 1(a ＞b ＞0),F1(-c,0)、F2(c,0)是E 的左、右焦点,AB、CD 分别是E 过F1、F2的两条弦,kAB·kCD=或AB、CD 分别为E 的长轴与垂径,则|AB|+|CD|为定值

推论5给定椭圆E := 1(a ＞b ＞0),P 是以E 的两焦点F1、F2为顶点且离心率为为E 的离心率)的双曲线= 1(其中c2= a2-b2)上异于顶点的任一点,直线PF1和PF2与E 的交点分别为A、B 和C、D,则|AB|+|CD|为定值