高考题怎样改编（二）——函数篇

苏 玖

一、真题展现

（2019年江苏卷第14题）设f（x），g（x）是定义在R上的两个周期函数，f（x）的周期为4，g（x）的周期为2，且f（x）是奇函数.当x∈（0，2]时，f（x）=，g（x）=其中k＞0.若在区间（0，9]上，关于x的方程f（x）=g（x）有8个不同的实数根，则k的取值范围是

二、思维延伸

本题f（x）是幂函数与二次函数复合的函数，g（x）是一次函数与常函数整合的分段函数，涉及二次函数的对称性、函数的奇偶性、周期性、函数图象等基本性质.

先利用奇偶性，得f（0）=0，于是函数f（x）在[0，2]上的图象就是圆（x-1）2+y2=1 f（y（x≥）0在）在一x个轴周上期半x部∈[分-，2由，于2]f内（x的）函是数奇图函象数，，再因利此用，f周（x期）的性图，可象以关作于出原f点（x对）称在，所（0以，9就]上得出的函数图象.首先利用周期性研究函数g（x）=-与f（x）图象的交点情况，当x∈（1，2]时，g（x）的图象与f（x）的图象无交点，但是，由于周期性，在x∈（3，4]和x∈（7，8]上各有一个交点.再研究g（x）=k（x+2）（k＞0）与f（x）图象在x∈（0，1]的交点情况，利用直线与圆的位置关系来研究，但所限制的区间为（0，9]，只能考虑两个半周期，要想得出8个交点，还有6个交点，于是每个半圆必产生2个交点，即直线段y=k（x+2）（x∈（0，1]）与四分之一圆（x-1）2+y2=1（y≥0，0x≤1）有2个交点，所以圆心到直线的距离dr，即1，解之得，0k

图1

再利用函数图象与k的几何意义知当直线段通过点（1，1）时合适，因此得k≥，故k的取值范围为

根据解析式的代数特征，利用图形描述问题，分析问题和解决问题.如果将本题中“f（x）是奇函数”改为“f（x）是偶函数”，于是可以改编为：

改编1 设f（x），g（x）是定义在R上的两个周期函数，f（x）的周期为4，g（x）的周期为4，且f（x）是偶函数.当x∈[0，2]时，f（x）=，g（x）=中k＞0.若在区间（0，14]上，关于x的方程f（x）=g（x）有11个不同的实数根，则k的取

本题函数f（x）的图象几何意义是圆的一部分，如果将解析式改为二次函数，于是又可以有：

改编2 设f（x），g（x）是定义在R上的两个周期函数，f（x）的周期为4，g（x）的周期为2，且f（x）是奇函数.当x∈（0，2]时，f（x）=-x2+2x，g（x）=其中k＞0.若在区间（0，9]上，关于x的方程f（x）=g（x）有8个不同的实数根，则k的取值范围是

如果利用圆与椭圆图形的一部分构造分段函数f（x），再结合相关性质，可以有：

改编3 已知f（x）是最小正周期为4的偶函数，函数g（x）=kx（x∈R），当x∈[0，2]时，f（x）=若在区间（0，10]上，关于x的方程f（x）=g（x）有9个不同的实数根，则正数k的取值范围是

注意结合图形充分利用圆的几何性质较为简单，前面几道题函数f（x）的最小正周期都是给定的，但也可以隐含在题干中，于是又可以有：

改编4 已知定义在R上的偶函数f（x），满足f（1-x）=f（1+x），当x∈[0，1]时，f（x）=x2，函数g（x）=ax+a（a≠0），对于给定的正整数n，关于x的方程f（x）=g（x）在区间[2n-1，2n+1]上有两个不同解，求a的取值范围.

如果将“偶函数”改为“奇函数”，再改变g（x）的解析式，于是问题又可以改编成：

改编5 已知定义在R上的奇函数f（x），满足f（1-x）=f（1+x），当x∈[0，1]时，f（x）=x2，定义在R上且最小正周期为4的函数g（x），g（x）=a≠0，若在区间（0，15]上，关于x的方程f（x）=g（x）恰有15个不同解，求a的取值范围.

本题将函数的奇偶性、对称性、周期性、函数图象整合在一起考查，利用这些性质证明f（x）是周期函数，如果函数f（x）的解析式无法求出，又会怎样出题呢？

改编6 已知定义在R上的奇函数f（x），满足f（1-x）=f（1+x），f（-1）=0，且f（x）在区间（0，1）上单调递增，试求函数f（x）在[-2020，2020]上的零点个数.

此题是抽象函数，也可以将函数f（x）改编为对数函数类型，再与周期函数结合，可以有：

改编7 设f（x），g（x）是定义在R上的两个周期函数且周期都是4，f（x）是偶函数.当x∈（0，2]时，f（x）=ln（x+1），g（x）=其中k＞0.若在区间（0，10]上，关于x的方程f（x）=g（x）有8个不同的实数根，则k的取值范围是

此题函数f（x）是对数类函数，有没有可能是指数类函数呢？

改编8 设f（x），g（x）是定义在R上的两个周期函数且周期都是4，f（x）是偶函数.

当x∈[0，2]时，f（x）=ex，g（x）=

其中k＞0.若在区间[0，n]（n∈N*）上，关于x的方程f（x）=g（x）恰有12个不同的实数根，求n的最小值及k的取值范围.

本题利用导数求指数函数的切线斜率，也可以改编为三角函数的问题，于是，

改编9 设f（x），g（x）是定义在R上的两个周期函数，f（x）的周期为4，g（x）的周

期为2，且f（x）是奇函数.当x∈（0，2]时，f（x）=2sin

其中k＞0.若在区间[0，12）上，关于x的方程f（x）=g（x）有12个不同的实数根，则k的取值范围是

三、点拨解析

f（x），g（x）在一个周期内的图象可知，直线g（x）=1与f（x）的图象只有一个交点，于是在区间（0，14]上，直线g（x）=1与f（x）的图象交点存在范围为（2，4）、（6，8）、（10，12）.要使得在区间（0，14]上有11个不同的交点，因此当0x≤2时，g（x）=k（x+2）与f（x）的图象必有两个交点，即直线与圆弧=4（0x≤2，0y≤2）必有两个交点，

改编2解析：根据f（x），g（x）在一个周期内的图象可知，直线g（x）=与f（x）的图象只有一个交点，再根据g（x）的周期为2，结合函数图象，直线g（x）=与f（x）的图象交点存在范围为（1，2）、（5，6）.要使得在区间（0，9]上有8个不同的交点，因此当0x≤1时，g（x）=k（x+2）与f（x）的图象必有两个交点，因此问题转化为方程f（x）=g（x）在区间（0，1]上有两个不同的解，即x+（k-2）x+2k=0在（0，1]上有两个不同的解，令h（x）=

2 x2+（k-2）x+2k，再根据二次函数图象分析知Δ＞0且h（0）＞0且h（1）≥0且0

改编3解析：因为f（x）是最小正周期为4的偶函数，因此对于任意整数n，当x∈[4n-1，4n+1]时，f（x）=2，当x∈[4n+1，4n+3]时，f（x）=，其几何意义是在相应的区间上分别表示椭圆（短轴在x轴上）和圆（直径在x轴上）的上半部分，函数g（x）=kx（x∈R）的几何意义表示过原点的直线.要使关于x的方程f（x）=g（x）在区间（0，10]上有9个不同的实数根，根据函数图象及k为正数，必有直线y=kx与半椭圆（x-8）2+=1（y≥0）有两个不同交点，且与半圆（x-10）2+y2=1（y≥0）无公共点，因此有（x-8）2+=1在[7，9]上有两个不同解，且圆心（10，0）到直

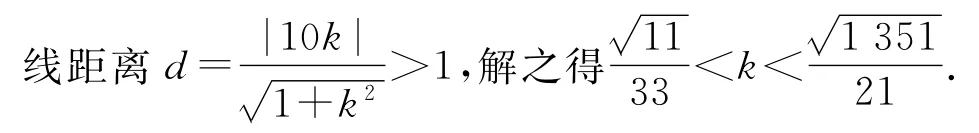
改编4解析：由f（x）是偶函数，满足f（1-x）=f（1+x），可以得出f（x）是周期为2的函数，于是x∈[2n-1，2n+1]时，f（x）=（x-2n）2.若从方程观点出发，将问题转化为a（x+1）=（x-2n）2，即x2-（4n+a）x+4n2-a=0在区间[2n-1，2n+1]上有两个不同解，再利用二次函数图象分析法可知0a

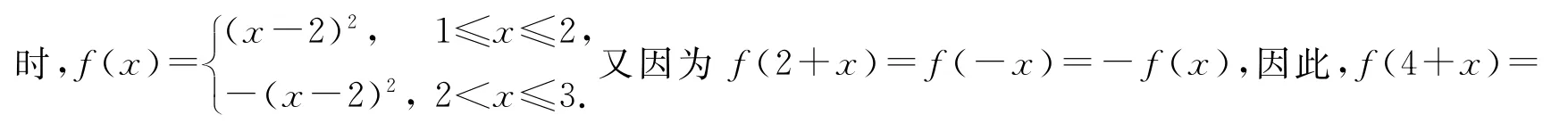
改编5解析：由f（x）是奇函数，满足f（1-x）=f（1+x），可以得出f（x）的图象关于直线x=1对称.由题意可得，当x∈[-1，0]时，f（x）=-x2，再根据对称性，当x∈[1，3]-f（2+x），所以f（x+4）=f（x），即f（x）是周期为4的函数.结合函数图象知，方程f（x）=-在区间[2，4]、[6，8]、[10，12]分别有两个不同解，而在[14，15]仅有一解.要使方程f（x）=g（x）在区间（0，15]恰有15个不同解，方程f（x）=a（x+1）（a≠0）在区间（0，2]必有2个不同解，再利用几何直观想象，因此，a的取值范围为0a.

改编6解析：由改编5的解析过程可知，函数f（x）的最小正周期为4且f（0）=0.因为f（-1）=0，因此，f（1）=0，f（2）=0，f（3）=0，f（4）=0.再结合f（x）在区间（0，1）上单调递增，因此f（x）在（0，4]上有且仅有4个不同零点.又（0，2020]上有505个周期，于是f（x）在（0，2020]上有2020个零点.由对称性知f（x）在[-2020，0）上也有2020个零点.故f（x）在[-2020，2020]上共有4041个零点.

改编7解析：根据函数性质和图象，可以判断方程f（x）=g（x）在（2，4）和（6，8）上各有一个解，因此方程f（x）=g（x）在区间（0，2）、（4，6）、（8，10）上各有两个不同解，所以f（x）=g（x）在（0，2）上必有两个解，利用导数知识求解，问题转化为过点（-1，0）作函数f（x）=ln（x+1）（0x2）的切线，设切点为（x0，y0），f′（x）=，即x0=e-1，因此切线斜率为k=.再结合函数图象，直线y=k（x+1）过点（2，ln3）时，直线斜率k=，故k的取值范围为≤k.

改编8解析：由函数性质和图象知，方程f（x）=g（x）在（2，4）、（6，8）、（10，12）等区间上各有一个解，要使n的值最小，必须使方程f（x）=g（x）在区间（0，2]、（4，6]、（8，10]等上各有两个不同解，所以，在（0，4]上有三个不同解.现在求过原点作函数f（x）=ex（x∈（0，2））的切线斜率，设切点为（x0，y0），f′（x）=ex，因此，即x0=1.于是切线斜率为k0=e，当直线y=kx过点（2，e2）时斜率为k1=.故k的取值范围为ek≤又f（x）=g（x）在（14，16]区间上的一解在（15，16）的范围内，则n的最小值为16.

改编9解析：根据函数图象和性质得，方程f（x）=g（x）在（3，4）、（7，8）、（11，12）等区间上各有一个解，同时x=0、2、4、6、8、10是方程的解，所以方程f（x）=g（x）在（0，1]、（4，5]、（8，9]等区间上各有一个解.根据函数的周期性，现在研究在原点处作函数f（x）=2sin（0x1），因为f′（x）=πcos，因此f′（0）=π.当直线y=kx过点（1，2）时，k=2.故k的取值范围为2≤kπ.

四、回顾悟道

在函数的学习和研究中，一般从整体和局部两个方面解释函数性质.一是函数的整体性质，如函数的定义域和值域（包括最值）、奇偶性、单调性、对称性、周期性、利用已知函数构造新函数；二是函数的局部性质，高中阶段主要学习的是导数的定义及几何意义，运用导数研究函数的性质，如单调性、极值点、极值、最值、函数图象、函数零点等.本题的一系列改编题不仅涉及函数的一些基本性质，同时也涉及二次函数、一次函数、无理函数、分段函数、指数函数、对数函数、三角函数、直线方程、圆的方程、椭圆方程、抛物线及导数等基本知识.

五、小试牛刀

改编提示：函数定义域是函数三要素的核心内容，也是高考常考的题型.求函数定义域实质就是转化为解不等式或不等式组，如果改为已知定义域或值域，求参数的取值范围.

（改编3）已知函数y=log2（ax2-ax+1）.

（1）若定义域为R，求实数a的取值范围；

（2）若值域为R，求实数a的取值范围.

解析

原题解析：问题等价转化为7+6x-x2≥0，利用二次函数f（x）=7+6x-x2的两个零点-1和7，结合二次函数图象，得-1≤x≤7，故定义域为[-1，7].

改编1解析：由题意得，（a2-1）x2-（a-1）x+1≥0的解集为R，于是分类讨论：

当a=1时，合适；当a=-1时，不等式为2x+1≥0，解集不是R；当a2-1＞0，即a＞1或a-1时，Δ=（a-1）2-4（a2-1）≤0，解之得a＞1或a≤-.综上所述，a的取值范围为a≥1或a≤-

改编2解析：由题意得，ax2+2x+1≠0恒成立，即ax2+2x+1=0无解.当a=0时，方程有解；当a≠0时，Δ=4-4a0，即a＞1.故a的取值范围为a＞1.

改编3解析：（1）由题意知，ax2-ax+1＞0的解集为R，下面分类讨论：当a=0时，合适；当a≠0时，必有a＞0且Δ=a2-4a0，即0a4.所以a的取值范围为0≤a4.

（2）由题意知，真数ax2-ax+1取一切正数，当a≤0时，不成立；当a＞0时，Δ=a2-4a≥0，解之得a≥4.所以a的取值范围为a≥4.

解题回顾 函数内容不仅是高中数学内容的主线，并贯穿于整个高中阶段始终，同时也是大学数学的基础，因此，备受高考命题人员青睐.在高考试题中，以基本函数为背景的高考试题层出不穷，常考常新，既能有效考查学生的等价转化能力，又可以考查学生利用函数图象分析问题和解决问题的能力，同时又能有效培养学生的直观想象核心素养.