有关不等式的“知识链”解读

江苏省扬州中学 姜卫东

不等式是刻画现实世界中不等关系的数学工具，它是描述优化问题的一个主要模型.依我们学过的知识来看，其实它在整个高中数学中也是一个重要的工具，在各类测试中都会有所涉及，一般以客观题的形式考查单纯的不等式知识，有时也以解答题的形式深度考查不等式与其他知识的融合.下面我们通过例题来看一看有关不等式的美丽的“知识链”.

一、一元二次显身手，解不等式不用愁

解析 因为x2-2x0，所以x（x-2）0，所以0x2，所以A=，所以A∩B=[1，2）.

变式1 不等式x2-2的解集

感悟 解不等式问题，关键在于利用同解变形，将原不等式向一元二次不等式转化.当然，在变式1中，也可对x进行分类讨论，去掉绝对值符号再求解，细细品味，又是另一番美丽.

变式3 关于x的不等式x2-2ax-8a20（a＞0）的解集为（x1，x2），且x2-x1=15，则a

解析 由题意得x1+x2=2a，x1·x2=-8a2，x2-x1=15，解得a=或-（舍去）.

感悟 已知解集求参数问题，应根据一元二次不等式与一元二次方程的关系列出关于参数的方程（组）.

变式4 解关于x的不等式ax2+（a-1）x-1＞0.

解析 原不等式可化为（ax-1）（x+1）＞0.

（1）当a=0时，原不等式为-x-1＞0，解集为（-∞，-1）.

（2）当a≠0时，方程（ax-1）（x+1）=0的两根为-1.考虑到二次项系数a的正负性及两个根的大小关系，还需继续分类讨论.①当a＞0时，有-1，原不等式的解集为（-∞，-1）∪；②当-1a0时，有-1，原不等式的解集为）；③当a-1时，有＞-1，原不等式的解集为）；④当a=-1时，有-1，原不等式的解集为∅.

感悟 解含参数的一元二次不等式，需要分类讨论，讨论时要考虑二次项系数、Δ的正负性及两根的大小，分类时应遵循“不重”、“不漏”、“最简”的原则.

二、拆拼凑消齐上阵，最值问题全击破

例2 设a＞0，b＞0，ab=1，求a+2b的最小值.

变式1 设x＞0，y＞0，且x+4y=1，求xy的最大值.

变式2 若x＞0，y＞0，x+2y+2xy=8，求x+2y的最小值.

解析二 设x+2y=t，利用基本不等式建立关于t的不等式，由x+2y+x（2）y）=8得：8-（x+2y）=x（2y）≤ ，即：，解得t≥4，可验证“=”成立，所以（x+2y）min=4.

感悟 解法一是通过消元将原式转化为一元函数，再通过变形使某部分对应的积为定值，进而用基本不等式求最小值，体现了消元思想；解法二是通过基本不等式来构造关于t的不等式，求出t的范围，进而得到原式的最小值.

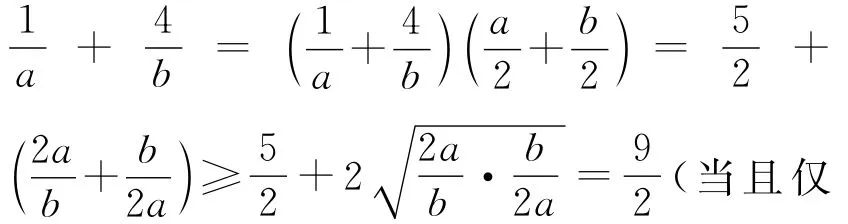
感悟 求最值问题，要注意借助“拆、拼、凑、消”等技巧，使其满足基本不等式中“一正”、“二定”、“三相等”的条件.