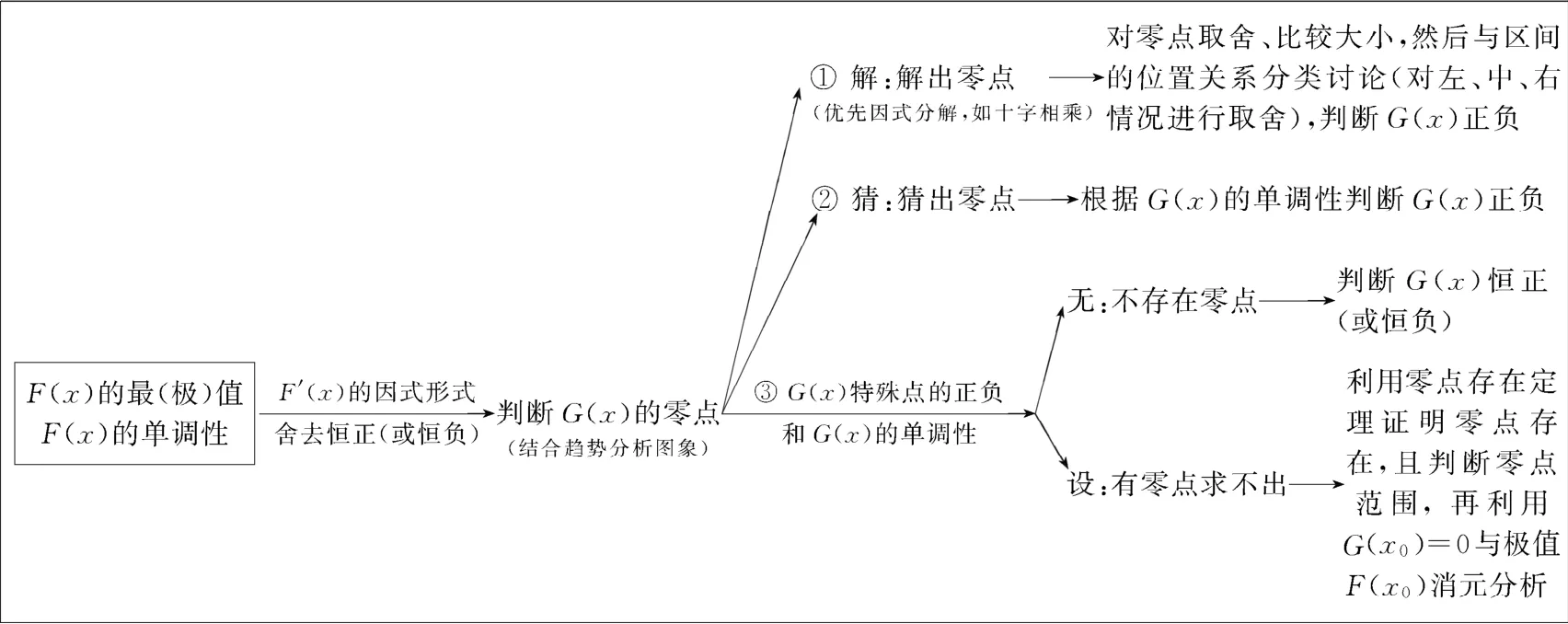
函数导函数零点和导数正负的判断

南京市教学研究室 龙艳文

函数导函数零点和导数正负的判断是判断函数单调性的关键.利用导数研究函数的单调性和极（最）值问题，通常先对函数求导，再令导函数为零，从而求零点.但若导函数含有参数或所得方程为超越方程时，零点分类比较复杂，符号难以判定，甚至零点无法求出，从而解题陷入困境.我们通过对一组问题的归类研究，从零点判断的各种情形中找出共同规律，提炼出有章可循的函数导函数零点和导数正负判断的途径和方法，从而构建导函数零点和导数正负的判断的解题思维模式结构图.

一、解题思维模式形成

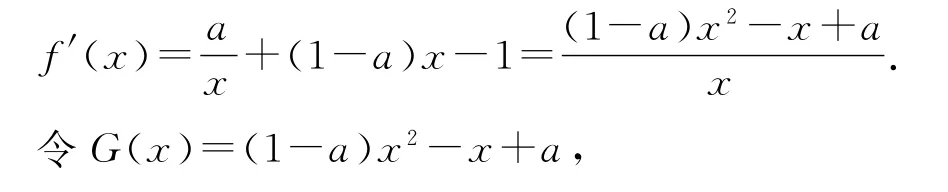
求导并通分，舍去恒正部分，令G（x）=（1-a）x2-x+a

① 当a=1时，G（x）=-x+1，当x∈（1，2）时，G（x）0，即f′（x）0，则f（x）在（1，2）上单调递减，所以[f（x）]min=f（2）=ln2-2.

判断二次项系数为0的情形

②当a≠1时，由G（x）=（x-1）[（1-a）x-a]=0，

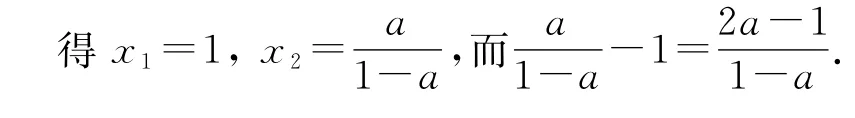
优先因式分解（如十字相乘），解出G（x）的零点

当x∈（1，2）时，G（x）＞0，即f′（x）＞0，则f（x）在（1，2）上单调递增，

对零点取舍、比较大小，再讨论在开区间（1，2）的左侧，结合G（x）的图象判断G（x）的正负

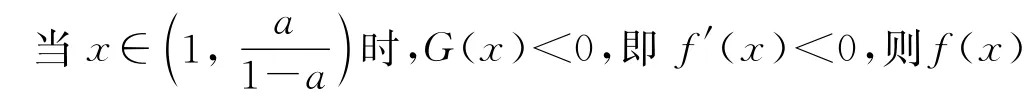
所以[f（x）]min=faln

对零点取舍、比较大小，再讨论在开区间（1，2）的中间，结合G（x）的图象判断G（x）的正负

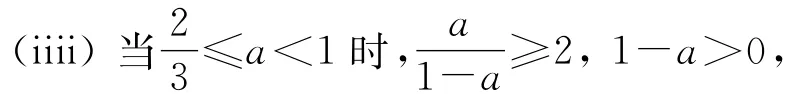
对零点取舍、比较大小，再讨论在开区间（1，2）的右侧，结合G（x）的图象判断G（x）的正负

综上，略.

思维模式结构图

对零点取舍、比较大小，然后与区间的位置关系分类讨论（对左、中、右情况进行取舍），判断G（x）正负

例2 已知函数f（x）=x2-ax，g（x）=lnx.若对任意x＞0，f（x）≥g（x）恒成立，求实数a的取值范围.

求导并通分，舍去恒正部分，令G（x）=x2+lnx-1

令G（x）=x2+lnx-1，

则G（1）=0.

猜出G（x）的零点

上单调递增.

当x∈（1，+∞）时，G（x）＞0，即F′（x）＞0，所以F（x）在（1，+∞）上单调递增.

所以F（x）的最小值为F（1）=1，

根据G（x）的单调性判断G（x）的正负

所以a的取值范围为（-∞，1].

思维模式结构图

令G（x）=2x2+3x-lnx-1，x∈（0，1]，

求导并通分，舍去恒正部分，令G（x）=2x2+3x-lnx-1

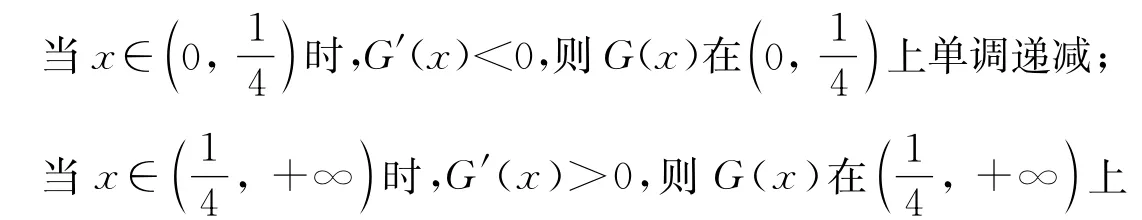
判断G（x）的单调性及特殊点（如端点、极值点等）正负

单调递增；

所以G（x）min=G

所以G（x）＞0在x∈（0，1]上恒成立，

所以F（x）在（0，1]上单调递增.

判断G（x）无零点，判断G（x）恒正综上，F（x）的最大值为1.

思维模式结构图

例4 （1）已知函数f（x）=lnx，g（x）=ex，试比较g（x）与f（x）+2的大小，并给出证明.

证明：令F（x）=g（x）-f（x）-2=ex-lnx-2，则

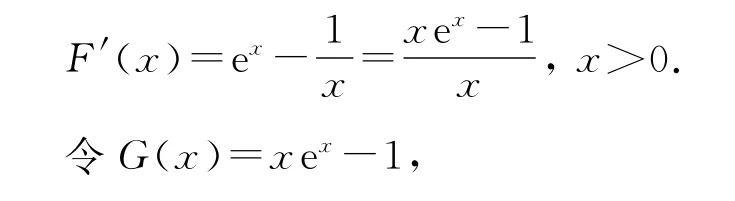
求导并通分，舍去恒正部分，令G（x）=xex-1则G′（x）=ex（x+1）＞0，

所以G（x）在（0，+∞）上单调递增，

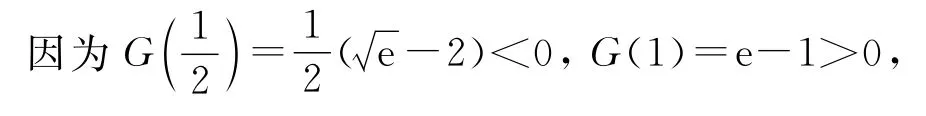
判断G（x）的单调性及特殊点正负

所以G（x）在（0，+∞）上存在唯一零点x0，且G（x0）=x0ex0-1=0，x0

利用零点存在定理证明零点存在，且判断零点范围

当x∈（0，x0）时，G（x）0，即F′（x）0，所以F（x）在（0，x0）上单调递减；

当x∈（x0，+∞）时，G（x）＞0，即F′（x）＞0，所以F（x）在（x0，+∞）上单调递增；

所以F（x）min=F（x0）=ex0-lnx0-2.

由G（x0）=x0ex0-1=0，得lnx0=-x0，

所以F（x0）=ex0-lnx0-2=

所以F（x）≥F（x0）＞0.

综上，g（x）＞f（x）+2.

设零点为x0，利用G（x0）=0与极值F（x0）消元分析

恒成立，求k的最大值.（参考数据ln8≈2.08，ln9≈2.20，ln10≈2.30）

求导并通分，舍去恒正部分，令G（x）=x-2lnx-4

设G（x）=x-2lnx-4，

当x∈（2，+∞）时，G′（x）＞0，所以G（x）在（2，+∞）上为增函数.

判断G（x）的单调性及特殊点（如端点、极值点等）正负

所以G（x）在（2，+∞）上存在唯一零点x0，

且G（x0）=0，即x0-2lnx0-4=0，x0∈（8，9）.

利用零点存在定理证明零点存在，且判断零点范围

当x∈（2，x0）时，G（x）0，即F′（x）0，所以F（x）在（2，x0）上单调递减，

当x∈（x0，+∞）时，G（x）＞0，即F′（x）＞0，所以F（x）在（x0，+∞）上单调递增.

所以F（x）的最小值F（x0）=

因为x0-2lnx0-4=0，所以F（x0）=∈（4，4.5）.故所求的整数k的最大值为4.

设零点为x0，利用G （x0）=0与极值F（x0）消元分析

思维模式结构图

利用零点存在定理证明零点存在，且判断零点范围，再利用G（x0）=0与极值F（x0）消元分析

二、解题思维模式构建

三、解题思维模式应用

例5 已知函数f（x）=x2-x-xlnx，证明：f（x）存在唯一的极大值点x0，且e-2f（x0）2-2.

证明：由f（x）=x2-x-xlnx，则f′（x）=2x-2-lnx.设G（x）=2x-2-lnx，

求导，令G（x）=2x-2-lnx

又G（e-2）＞0，G0，G（1）=0，

判断G（x）的单调性及特殊点（如端点，极值点等）正负

利用零点存在定理证明零点存在，且判断零点范围

当x∈（0，x0）时，G（x）＞0，即f′（x）＞0，所以f（x）在（0，x0）上单调递增；

当x∈（x0，1）时，G（x）0，即f′（x）0，所以f（x）在（x0，1）上单调递减；

当x∈（1，+∞）时，G（x）＞0，即f′（x）＞0，所以f（x）在（1，+∞）上单调递增；

所以x=x0是f（x）的唯一极大值点.

由f′（x0）=0，得lnx0=2（x0-1），故f（x0）=-x0-x0lnx0=x0（1-x0）.

由x0∈（0，），得f（x0）.

因为x=x0是f（x）在（0，1）的最大值点，由e-1∈（0，1），得f（x0）＞f（e-1）=e-2.

所以e-2f（x0）2-2.

利用G（x0）=0与极值F（x0）消元分析

四、解题思维模式练习

1.求证：ex＞lnx+2.

4.已知函数f（x）=lnx，设g（x）=ex-f（x），记g（x）的最小值为d，求证：2de.

（1）求L的方程；

（2）证明：除切点（1，0）之外，曲线C在直线L的下方.

1.略. 2.kmax=3. 3.略. 4.略. 5.（1）L的方程为y=x-1. （2）略. 6.ab=1.7.略.