含参数的一元二次不等式的解法突破

南京市金陵中学 于 健

求含参数的一元二次不等式的解集是我们学习这部分内容的难点，首先要搞清楚不含参数时如何解不等式，虽说有几种不同的解法，但其核心可以归纳为“一求、二画、三写”三步曲.即先求相应的一元二次方程的根，然后画出相应的一元二次函数的草图，最后写出不等式的解集.它将三个“二次”（二次不等式、二次方程、二次函数）之间的关系有机地结合起来，数形结合跃然纸上.

而解含参数的一元二次不等式，仍可围绕“一求、二画、三写”这三步曲，但是由于不等式中含有参数，就要考虑：对应的方程是否有根？在画相应的函数的草图时，图象是抛物线吗？开口如何？方程如有两根，谁大谁小？以解ax2+bx+c＞0为例，因为a，b，c中会含有参数，所以以上情况，就需要分类讨论了.

一、不等式的“身份”明确，对应方程的根的情况明显

当参数不包含在二次项系数处时，我们可以把它称之为“身份”明确的不等式.对于这种含参的一元二次不等式，当其对应方程的根的情况也很明显时，我们就只需要对方程的根的大小关系做出分类讨论即可，从而再依据之前总结的一般一元二次不等式的解法，在不同的分类讨论标准下写出对应的解集.

例1 解关于x的不等式x2-）+10（a≠0）.

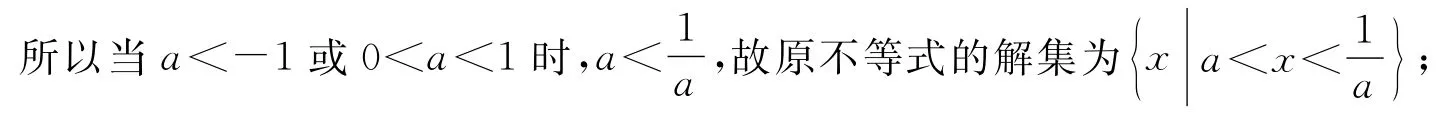
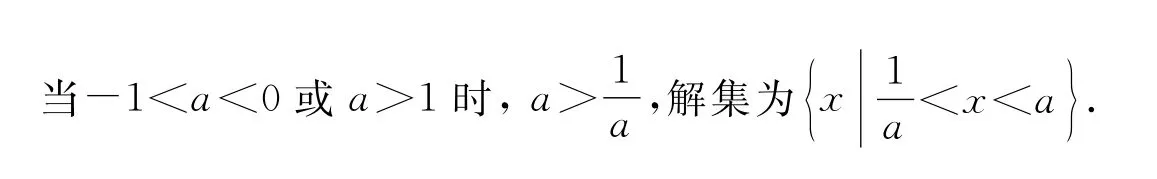
二、不等式的“身份”明确，对应方程的根的情况不明显

当我们讨论的是“身份”明确的含参的一元二次不等式，但其对应方程的根的情况却不明朗时，我们分类讨论的标准应是对应的一元二次方程的根的判别式的符号，从而再依据之前总结的一般一元二次不等式的解法，在不同的分类讨论标准下写出对应的解集.

例2 解关于x的不等式：x2+ax+4＞0.

分析 本题中由于x2的系数大于0，但是方程x2+ax+4=0的根的情况不明显.故需考虑方程的根的判别式Δ的情况.

解 因为Δ=a2-16，所以当a∈（-4，4），即Δ0时，解集为R；

三、不等式的“身份”不明确

当不等式中的二次项系数包含参数时，我们可以把它称之为“身份”不明确的不等式.对于这种含参的不等式，首先是对二次项系数为正、负或0展开讨论.若二次项系数为0时就是一元一次不等式，可以首先写出其解集；但当其二次项系数不为0时，相应的一元二次方程的根的大小，有时容易比较大小，更多时候方程的根的大小与参数有关，这时就需要再分级讨论了.

例3 解关于x的不等式：

（1）ax2+（a+2）x+1＞0；

（2）[（m+3）x-1]（x+1）＞0（m∈R）.

分析（1）中二次项系数含有参数a，Δ=（a+2）2-4a=a2+4＞0，故只需对二次项系数进行分类讨论；（2）中因为不等式的二次项系数为m+3，当m+3=0时，原不等式可化为x+10，原不等式的解集为：｛x|x-1｝；当m+3≠0时，不等式为二次不等式，需将不等式化为（x-x1）（x-x2）＞0（或0）的形式，两边同除以m+3，因其符号不确定，要保证不等式的同解变形，所以还应考虑m+3的正负号，同时还要考虑比较方程两个根的大小.

若a≠0，因为Δ=（a+2）2-4a=a2+4＞0，解得方程ax2+（a+2）x+1=0两根x1=（2）① 当m+3=0时，原不等式可化为x+10，原不等式的解集为：｛x|x-1｝；解集为或x

当m=-4时，原不等式解集为∅；

通过以上总结分析，探求含参数的一元二次不等式的解集的过程中，最重要的是分类讨论这一基本数学思想的正确应用.解题时同学们一定要克服畏惧心理，冷静分析，厘清分类标准，恰当分类，相信自己一定能解答好.