类比法解决数列新问题

江苏省丹阳市第五中学 孔帮新

等比数列相比等差数列而言，似乎更“难”一些；但是，正因为已经学习了等差数列，因此我们可以运用类比的方法来征服等比数列的新领域.

一、等比特征非零

从等比数列的定义看，等比数列的任意项都是非零的，而且公比q也是非零常数.这一点很容易被忽略.但在等差数列中就不存在这一担心点，可以对比考虑来提高辨识度.

如，考虑：（1）在等比数列｛an｝中，是否有=an-1an+1（n≥2）？（2）如果数列｛an｝中，对于任意的正整数n（n≥2），都有=an-1an+1，那么，｛an｝一定是等比数列吗？

思考：（1）因为｛an｝是等比数列，所以，即=an-1an+1（n≥2）成立.

显然，“0”这个因素在作怪.因此，我们可将（2）修改为下面正确的结论：

当一个数列｛an｝中的各项都不为0时，若=an-1an+1，则数列｛an｝是等比数列.

但有时条件比较隐蔽，需要我们细心观察.

思考：由x，3x+3，6x+6成等比数列得 （3x+3）2=x（6x+6）.解得x1=-3或x2=-1.但x2=-1时第2项为零，不合题意，必须舍去，故数列的第4项为-24.

二、函数方程显威

学习等差数列时，相信很多同学已经见识到函数这个武器的威力了.同样地，利用函数、方程的观点和方法，可以轻松揭示等比数列的特征及基本量之间的关系.一般说来，函数与数列的结合，也是基本量思想大放异彩的时机，将五个基本量中的某一个视为自变量x，则可转化为函数问题来求解.

例1 等比数列｛an｝的前n项和为Sn，已知S1，S3，S2成等差数列.

（1）求｛an｝的公比q；

（2）若a1-a3=3，求Sn.

解 （1）依题意有a1+（a1+a1q）=2（a1+a1q+a1q2），由于a1≠0，故2q2+q=0，解这个一元二次方程，注意到q≠0，从而q=.

（2）由已知可得a1-a1=3，故

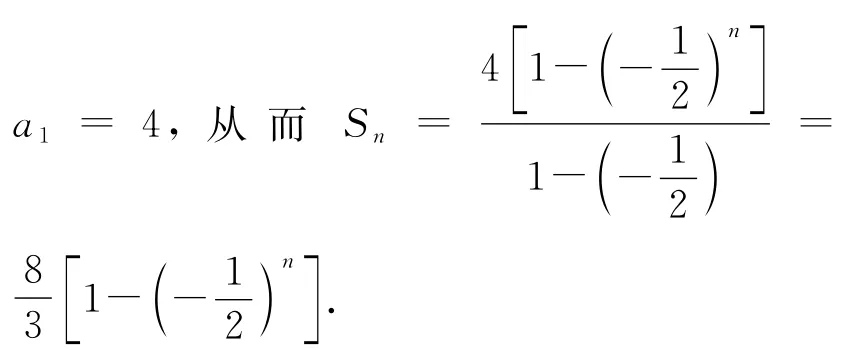
得到的前n项和Sn是一个关于项数n的指数函数关系式，联系相关知识，还可以作很多变式，同学们可以自行探究.

提到函数性质，当然少不了单调性.在借用指数函数讨论等比数列的单调性时，要特别注意首项和公比的大小.

一般来说，a1＞0时，若q＞1，则等比数列是递增数列；若0q1，则等比数列是递减数列.

要注意的是不能简单地将等比数列的单调性等同于指数函数的单调性，毕竟等比数列只能算作自变量是取自正整数集的函数.

三、前n项和细琢磨

等比数列的前n项和公式是用错位相减法求得的，我们可以细细琢磨这种方法在数列求和中的运用.

例2 求和：Sn=x+2x2+3x3+…+nxn（x≠0）.

解 分x=1和x≠1两种情况.

当x=1时，Sn=1+2+3+…+

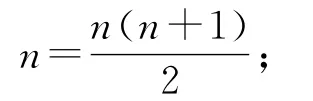
当x≠1时，Sn=x+2x2+3x3+…+nxn，

xSn=x2+2x3+3x4+…+（n-1）xn+nxn+1，

所以（1-x）Sn=x+x2+x3+…+

综上可得，

很多同学做这道题时会忽略“x=1”这个情况，或者会有疑问，觉得在题干中看不到需要分情况讨论的迹象.所谓冰冻三尺，非一日之寒，做题的题感得之不易，需要对这类题作出非常细心、详尽的探究和思考，此题中“x=1”这个情况就可看作是熟练之后的水到渠成.

分“q=1”和“q≠1”两种情况化简时，还要注意整体代换思想，这样可以让我们少走许多弯路.

例3 设首项为正数的等比数列｛an｝的前n项和为80，它的前2n项和为6560，且前n项中数值最大的项为54，求此数列的第2n项.

解 设数列｛an｝的公比为q，若q=1，则Sn=na1，S2n=2na1=2Sn.

因为S2n=6560≠2Sn=160，所以q≠1.

将①整体代入②得80（1+qn）=6560，得qn=81.

将qn=81代入①得a1（1-81）=80（1-q），即a1=q-1，由a1＞0，得q＞1，即数列｛an｝为递增数列.又因an=a1qn-1=-1联立可得a1=2，q=3，所以a2n=2×32n-1（n∈N*）.

四、判定方法择优

常用的等比数列的判定方法有：

（2）等比中项法：a2n+1=anan+2（an≠0，n∈N*）；

（3）通项法：an=a1qn-1（a1q≠0，n∈N*）.

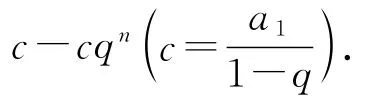
例4 已知数列｛an｝的前n项和为Sn，数列｛bn｝中，b1=a1，bn=an-an-1（n≥2），且an+Sn=n.

（1）设cn=an-1，求证：｛cn｝是等比数列；

（2）求数列｛bn｝的通项公式.

分析 一般来说，遇到通项与前n项和一起组成的关系式时，常将项数n变成n-1（或n+1），得到另一个关系式，相减即得相邻两项或三项之间的递推关系，必要时再构造数列求解.本题中，显然是要去构造｛an-1｝这个数列.

解 （1）证明：因为an+Sn=n，①

所以an+1+Sn+1=n+1.②

②-①得2an+1=an+1，构造数列｛an-1｝，将前式整理得2（an+1-1）=an-1.｛an-1｝是等比数列.

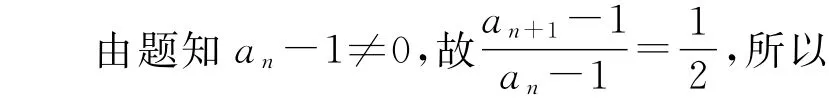
又a1+a1=1，得a1=，首项c1=a1-1=-，公比q=.

又cn=an-1，即｛cn｝是以为首项，为公比的等比数列.

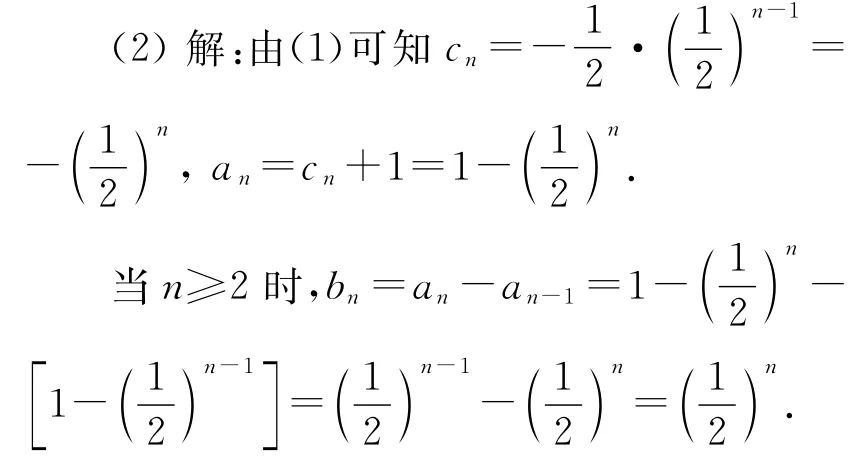
又b1=a1=代入上式也符合，所以

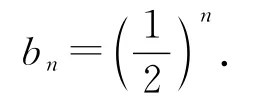
该题第（1）问中的解题方法是需要我们透彻掌握的，是前n项和与通项之间的紧密联系的体现，熟练以后，我们要能自然而然地发现｛an-1｝这个等比数列；另外第（2）问中要注意验证n=1时是否符合n≥2时的通项公式，等比数列一般会含有指数项，能合并的必须合并.

例5 已知等比数列｛an｝的前n项和

解法一 运用特殊值法.

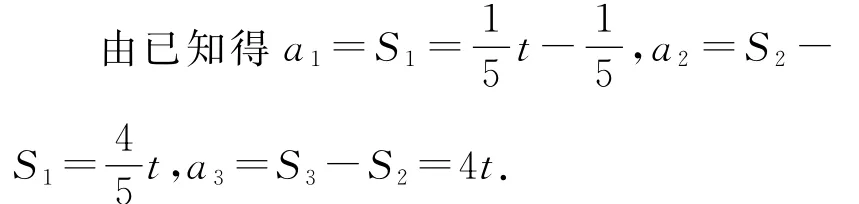
因为｛an｝是等比数列，所以）×4t，显然t≠0，所以t=5.

解法二 运用等比数列前n项和公式的结构特征.

因为等比数列前n项和Sn=（1-qn），即具有Sn=c·（1-qn）的形式.

将Sn进行整理：Sn=-所以=1，即t=5.

在高考中数列题除了会出现在解答题以外，小题也一般会有它的身影.运用特殊值法是解决等比数列填空题的有效方法，有时运用等比数列前n项和公式的结构特征解决填空题也非常简捷.

有时候，要判断一个数列是不是等比数列，正向思维难以突破，我们可以尝试着逆向探究，试试前几项，能否满足等比数列的条件.例如an=2n+3n，发现这只是只“纸老虎”，徒有指数外表，但根本不是等比数列.