老师，我为什么算得这么慢——函数篇

江苏省苏州中学 王思俭

考试结束后，同学们又热议一阵子：

测验卷中含有绝对值求值问题，计算好复杂，结果还错了；

我也是计算6个f（x）的函数值，然后加起来，虽然做对了，但浪费时间；

含有绝对值的方程解的问题，运算量很大，不知道选择怎样的算法；

看来只顾刷题，不总结回顾解题方法和解题的思维过程，不能真正提高解决问题的能力；

在动手解题之前，先要分析题目的信息和结构特征，考虑选取怎样的解题策略；

……

为此，我邀请几位同学就“函数中的运算问题”进行交流，旨在引导学生如何提高数学运算能力.g（2）

生+甲…：+g（6题）的目值1 .已知函数f（x）=x2-9x+18，g（x）=f（x）+|f（x）|，求g（1）+

我是直接计算f（1）=10，f（2）=4，f（3）=0，f（4）=-2，f（5）=-2，f（6）=0，因此g（1）+g（2）+…+g（6）=20+8=28.

生乙：先化简再求值，先考虑怎样去掉绝对值，当f（x）≤0时，g（x）=0.利用因式分解，得f（x）=（x-3）（x-6），发现当3≤x≤6时，f（x）≤0，因此要求的值转化为2（f（1）+f（2））=28.

教师：若把函数f（x）的解析式改为“f（x）=x2-23x+60”，求g（1）+g（2）+…+g（20）的值，怎样求解呢？

生乙：直接计算是不是太麻烦了，还是考虑怎样去掉绝对值，先讨论f（x）≤0时，g（x）=0.因此，当x2-23x+60≤0，即3≤x≤20，所以g（3）=g（4）=…=g（20）=0，f（1）＞0，f（2）＞0，故原式=g（1）+g（2）=2（f（1）+f（2））=2×56=112.

教师：很好！生甲的方法是直接法，对于项数较少的求值题，运算量不大，但对于项数较多的求值问题，就要考虑先去掉绝对值，再求值.请看：

变题1 已知函数f（x）=-x2+676x-2019，g（x）=，求g（1）+g（2）+…+g（673）的值.

生丙：因为f（x）=-（x-3）（x-673），于是g（x）=因此，原式=f（1）+f（2）=-2015.

教师：很好！要寻找数字特征的关系，已知函数式中的2019与目标中的673的关系，于是就可以进行因式分解了，这样就便于化简.再看：

变题2 已知函数f（x）=x3-10x2-9x+90，g（x）=，求g（1）+g（2）+…+g（10）的值.

众生：三次函数式如何分解？

教师：你们想想所求式子中的最大自变量与函数式中常数项之间的关系是什么？能否大胆猜想函数式中含有因式x-10？

生丙：对f（x）=x3-10x2-9x+90进行因式分解得，f（x）=（x+3）（x-3）（x-10），因此，g（x）=因此，原式=f（1）+f（2）=112.

生乙： 题目2 已知函数f（x）=ax2+bx+c（a≠0）的图象过点（1，0），对任意x∈R都有不等式-x-3≤f（x）≤2x2+3x-1成立.

（1）求f（-1）的值；

（2）求f（x）的解析式；

（3）是否存在正实数m，使得函数y=mx+m2与函数g（x）=的图象交于三个不同的点？若存在，求出m的取值范围；否则，请说明理由.

第（1）（2）小题会做，函数f（x）=x2+x-2，但第（3）小题不会做了.

教师：你们是否要先化简函数式？然后尝试将两个函数图象有三个不同的交点问题等价转化为方程有三个解，再结合函数图象进行分析求解.

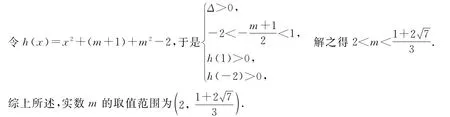
教师：正确！当直线与抛物线段有两个交点时，直线必与x轴上的射线有一个交点.同时，一元二次方程（二次项系数为正数）在指定开区间上有两个不同解的充要条件为判别式大于零且两端点函数值为正且对称轴在区间内等四个约束条件，问题就转化为解不等式组.请看：

（2）建筑过程管理信息化。“智能建筑”理念的深入人心，也使得建筑项目管理更加智能化，因此，现代建筑业发展尤其注重建筑工程项目管理，项目管理已经脱离了传统的纸质媒介，利用BIM技术在建筑项目中的管理，能够将建筑工程项目数据源建立起来，使得项目各参与方的相关信息准确性和一致性得到有效保障，实现建筑项目管理的信息交流与共享，极大地提升了建筑项目管理的信息化水平。

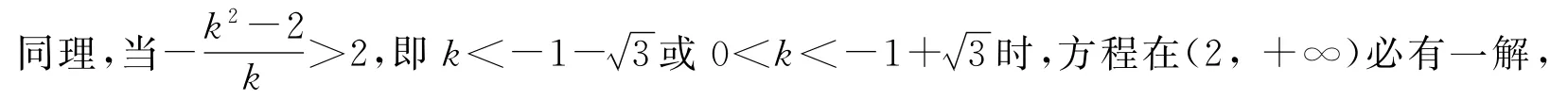
生戊：本题不要分得这么细，当k≠0时，直线y=kx+k2-2与y=g（x）的图象在（-1，2）内有两个不同交点，此时直线必与x轴有一个交点分布在（2，+∞）或（-∞，-1）上.于是只要探寻F（x）在（-1，2）内有两个零点的充要条件即可.

教师：很好！生戊的思路简洁明了，计算量较小.请看：

变题2 已知函数f（x）=-x3+3x2（x≥0），g（x）=.若方程g（x）=kx+4（其中k为实数）有3个不同解，求k的取值范围.

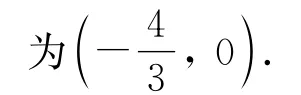
教师：正确！本题是三次函数的零点问题，利用导数，再借助函数图象求解.

关于函数问题中的数学运算要注意如下几个方面：

一是要充分理解函数的有关概念，注意函数的三要素（定义域、值域、解析式），函数的定义域是研究函数的核心知识点；

二是要熟悉函数的相关性质：奇偶性、单调性、周期性、对称性；

三是要掌握一些特殊函数，如二次函数、三次函数、反比例函数、指数函数与对数函数、对勾函数、含绝对值的函数等等；

四是要灵活运用函数性质、基本数学思想与方法求解，如整体思想、函数与方程、分类讨论、数形结合、等价转化等思想方法；

五是运算过程要简洁明了，不要拖泥带水，答案正确.

2.已知函数f（x）=x2-（2a+2）x+a2+2a-3，其中a 为实数，g（x）=.若方程g（x）=x+1有3个不同解，求a的取值范围.

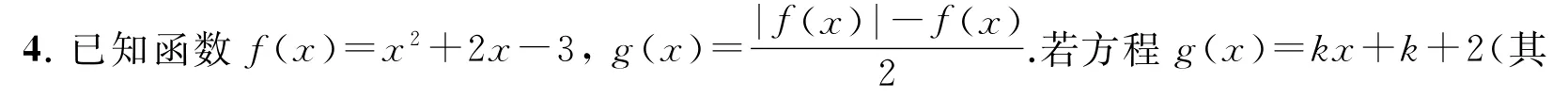
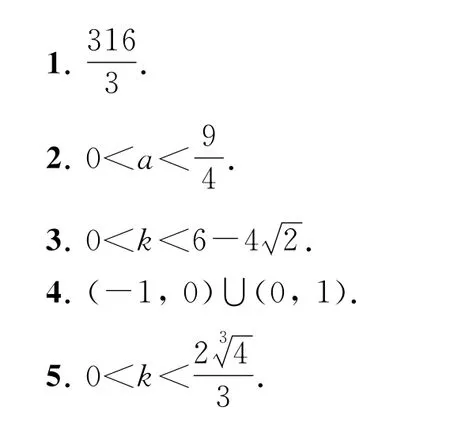
解.于是，令F（x）=x2+（k+2）x+k-1，利用二次函数图象分析法，其充要条件为解之得，-1k1.当k=0时，g（x）=2有且只有两个不同解，故k=0不满足条件，故k的取值范围为（-1，0）∪（0，1）.

另法：直观几何法，直线过点P（-1，2），抛物线弧的两个端点为A（-3，0）和B（1，0），要使方程有三个不同解，必须有kPBkkPA，而kPB=-1，kPA=1，且当k=0时，g（x）=2有且只有两个不同的解，故k≠0，所以，k的取值范围为（-1，0）∪（0，1）.