圆锥曲线

江苏省吴江盛泽中学 孙四周

大家肯定见过圆锥，知道圆锥的侧面和底面.现在请把注意力集中到圆锥的侧面，而把底面忽略掉.这个“没有底”的圆锥面，每一条母线都失去了限制，变成可以任意延长的射线，就得到一个无限的圆锥面.现在，把两个“相同的”圆锥面顶点重合在一起，使得它们的母线互为反向延长线，这样的两个圆锥面共同构成一个图形，向两方无限延伸（如图1），这就是数学上的圆锥面.

用一个平面来截圆锥面（不妨用手比画一下），能截出什么样的图形呢？现在，开动我们的想象力……继续想象……不难想到下面的结果（如图2的一组图）：

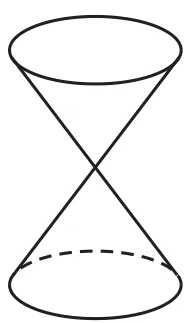
图1

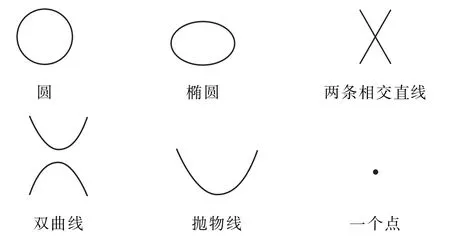
图2

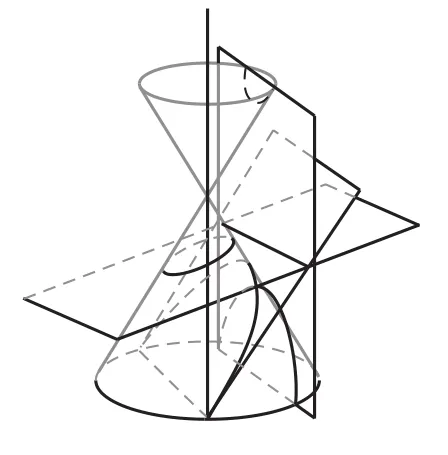
所有这些曲线，都是由平面截圆锥面得来的，但是我们只把其中的三种称为圆锥曲线，它们是：椭圆、双曲线、抛物线.苏教版数学教材上是这样说的：“椭圆、双曲线和抛物线统称为圆锥曲线.”根据这个定义，圆不是圆锥曲线，圆也不是特殊的椭圆.

它把圆排除在圆锥曲线之外，或许你对这个定义会觉得不爽，这没必要.“把×××统称为×××”型的定义，属于“逆式定义法”，很大程度上取决于人为规定.它就是把一类东西归一起，以便于称呼、便于交流.同样用逆式定义法给出的还有：“有理数和无理数统称为实数”“正弦函数、余弦函数、正切函数统称为三角函数”，等等.这里，“实数”的定义倒是把对象说全了，“三角函数”则只说了六种中的三种（历史上还曾有过余切、正割、余割）.

为什么教材不把圆当作特殊的椭圆？因为这会使后面的第一定义、第二定义等发生表述上的繁琐，增加思考的成本.目前国际上的教材基本都是这个态度，即不认为圆是椭圆的特例.当然，如果将来谁编教材时把圆归入圆锥曲线、归入椭圆，也是可以的（那将是一本很有特色但也很不清爽的教材）.

根据目前对圆锥曲线的定义，椭圆的离心率范围是开区间（0，1），没有圆的容身之地；椭圆的一个标准方程=1（a＞b＞0），也不包括圆.有人可能会说，当a=b时椭圆方程就是圆.这种形式上的趋同，太表面化了，不能据此改变更深层认知.其实，椭圆方程里已经明确规定a＞b＞0，“a=b”本身就是一个伪命题.

椭圆、双曲线、抛物线都有简洁、优美的方程，这是人为选择的结果.坐标系完全是人类构造出来的，它并不是圆锥曲线（也不是任何曲线）天然带来的，如果选择不同的坐标系，曲线就会有不同的方程，而曲线本身并不产生变化.比如我们知道的，反比例函数的图象就是双曲线，不是名词上的重合，y=的图象（也请比画一下）“就是”双曲线，它的渐近线是坐标轴，离心率等，实轴长等于；二次函数y=ax2+bx+c（a≠0）的图象“就是”抛物线……

圆锥曲线的研究，起始于2000多年前的古希腊，那时还没有坐标系（笛卡儿在近2000年后才出生），他们是用综合几何的方法（今日的平面几何）研究圆锥曲线的.当时阿波罗尼斯写了一本书，名叫《圆锥曲线》，已经把现在已知的关于圆锥曲线的几乎所有知识都囊括在内了，此后的人们所做的不过是改写和注释的工作.这是古希腊、也是全人类科学思想的光辉典范：他们研究科学不考虑任何物质的收获，仅仅是为了精神上的满足.那时的圆锥曲线看不出丝毫的实际用处，但是思想家的热情还是非常高.他们也曾经把圆锥曲线用于解决立方倍积和三等分任意角问题，效果异常，但那不会带来任何的经济利益，与GDP没有丝毫关系.

直到近代，天文学家（以开普勒为代表）发现行星轨道是椭圆，某些彗星的轨道是抛物线和双曲线，圆锥曲线才在科学上大放异彩.此时的科学家简直乐坏了，因为他们所需要的知识早已由阿波罗尼斯准备妥当！如果我们对思维的深层机制进行剖析，你一定会好奇于这样的事情：凭借着有限时间内对很短一段轨道的观察，开普勒是如何想到行星的轨迹是椭圆的呢？如果他头脑里没有椭圆的形象，要他从头开始构造出轨道是椭圆，这可能吗？我们可以做一个很自然的猜想：开普勒的头脑里先有了椭圆的形象，在研究行星轨道的时候发现哥白尼用的“正圆”不对，于是把椭圆用了起来，经过一番检验发现正好……

除了天文学上的应用外，圆锥曲线已经被用到机械、建筑、通信等多个方面.今日的GPS全球定位系统，计算的基础就是双曲线，如果没有双曲线将什么也不能做.空间通信技术实际上是数学技术，具体说是圆锥曲线的应用技术！关于圆锥曲线的光学性质也非常丰富非常有用，有兴趣的读者可以查阅相关资料.

曾经有人筛选过初等数学的难题，出了一个“百题榜”，其中之一是这样的：

日晷（以及圭表）的尖端，在地面上投影的轨迹是什么？

如果我们有圆锥曲线的定义，就很容易解决——简直一看便知.简述如下：太阳光线照在圭表指针的顶端，形成一条射线.当太阳旋转一周（其实是地球自转一周）后，这条光影形成一个圆锥面.该圆锥面与地面（近似看作平面）相交，截线就是你所要的轨迹，显然它是圆锥曲线.视该圭表在地球上的纬度以及太阳所在的位置（节气）而定，可能是椭圆，也可能是双曲线和抛物线（一定不会是圆）.

最后说句题外话.依据圆锥曲线的光学性质，人们实现了对光（包括电磁波以及其他的波）的控制和利用.目前还有一种波，是人们无法控制的，聪明的你也许一激灵：那是引力波！没错，就是引力波.引力波传递了宇宙间唯一的长程力，它是宇宙的实际控制者.我们非常渴望认识它，但是目前的认识还非常有限.2018年人类观测到了引力波，当即就被授予诺贝尔奖，简直有点急不可耐的味道！但是，仅此而已.大家知道，牛顿用三棱镜对光进行了分解，科学家又用圆锥曲线对光进行聚焦和散射.如果谁能对引力波做出这样的事情，哪怕只做出一点点，毫无疑问他就会获得诺贝尔奖，做出几个就能获得几项.

圆锥曲线，你还有多少用武之地？