Timoshenko方程组Cauchy问题光滑解的稳定性

侯宏乐，刘存明

(太原理工大学 数学学院, 山西 太原 030024)

0 引 言

本文研究的如下的Timoshenko方程组:

(1)

式中：t∈+；x∈是空间变量；φ(t,x)表示位移；ψ(t,x)表示角度；σ(y)是已知光滑函数且σ′(y)>0,γ>0为正常数. 赋予系统(1)如下的初值条件

t=0:(φ,∂tφ,ψ,∂tψ)=

(φ0(x),φ1(x),ψ0(x),ψ1(x)).

(2)

在有界区域, 文献[1]得到了当式(1)的第一个方程有-φt时,式(1)的解是指数稳定的, 文献[2] 中, 当式(1)的第一个方程无-φt时, 式(1)的解不是指数稳定的, 除非在等波速的情况下. 在整个空间上, 文献[3]借助傅里叶空间中的能量估计, 得到了在等波速和不等波速情形下的两个衰减估计. 文献[4]改进了文献[3]的结果. 文献[5]中, Racke和Houari 引入空间L1,r(), 改进了文献[3]的结果. 文献[2，6]用不同的方法得到了相似的结果.最近, 文献[7-8]在等波速和不等波速的情形下, 得到了系统 (1)在Besov空间中的整体解以及解的衰减估计. 文献[1，9-10]研究了带热传导及其他耗散类型的Timosh enko系统. 文献[11-12]考虑带记忆项耗散的情况. Ide和Kawashima在文献[13]中利用时间加权的能量估计获得整体解的存在性和解的衰减性.

1 主要结果

为了方便, 引入如下记号：H2,L2,L∞分别表示经典的Sobolev空间H2(),L2(),L∞(), 它们上面的范数分别记作‖·‖H2,‖·‖ 及‖·‖L∞；〈·,·〉表示Hilbert空间L2() 上的内积，C；Ci(i∈)均表示与时间变量t无关的正常数.

在文献[3]中，引入了如下的变量替换

u=∂tφ,v=∂xφ-ψ,y=∂xψ,z=∂tψ.

由式(1)可得到关于变量(u,v,y,z)的方程组:

(3)

并满足初始条件

t=0:(u,v,y,z)=(u0(x),v0(x),

y0(x),z0(x)),

(4)

其中

u0=φ1,v0=∂xφ0-ψ0,y0=∂xψ0,z0=ψ1.

U∈C([0,T*],H2())∩C1([0,T*],H1()),

其中，T*一般依赖于σ′(y).

对于Cauchy问题(3)～(4), 可以得到如下的整体存在性结果：

定理1存在常数δ>0, 使得对任意满足

的初值U0, Cauchy问题(3)～(4)存在唯一整体经典解U=U(t,x), 并且对任意的t≥0, 成立

2 对称化及能量估计

本节将方程组(3)写为一般形式的双曲方程组, 并利用对称化技巧对U进行能量估计, 最后对相应的变量作耗散能量估计.

2.1 方程组(3)的对称化

式(3)可写为如下一般形式方程组

∂tU+A(U)∂xU+LU=0,

(5)

并且满足如下初始条件

t=0:U=U0(x),

(6)

其中，U0=(u0,v0,y0,z0),

(7)

(8)

取

(9)

则A0(y)关于y是一致正定矩阵. 且

(10)

是对称矩阵. 从而方程组(5)是可对称化双曲方程组.

为了进行能量估计, 下面将用到经典的Sobolev嵌入定理H2()W1,∞(), 即存在一个常数Cem>0, 使得

‖f‖|L∞≤Cem‖f‖H2, ∀f∈H2().

(11)

2.2 能量估计

对任意T>0, 设U=U(t,x)是Cauchy问题(5)～(6)在区域[0,T]×上的H2解. 对任意t∈[0,T], 定义能量泛函ε2(t) 及耗散能量泛函D2(t)为

ε2(t)=〈A0(y)U,U〉+〈A0(y)∂xU,∂xU〉+

〈A0(y)∂x2U,∂x2U〉,

‖∂xu‖2).

不妨假设ε2(t) 充分小, 从而由经典Sobolev嵌入定理式(11), 得

‖y‖L∞≤C‖U‖H2.

这样就有

成立, 当|y|≪1时.

要证明定理1, 只需确立如下的能量不等式

(12)

利用对称化技巧及经典能量估计, 有如下的命题.

命题1对于任意的t∈[0,T], 成立

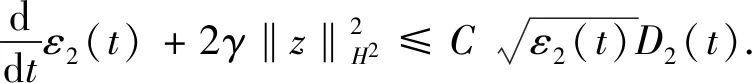
(13)

证明L2估计式(5)左乘矩阵A0(y), 并与U作L2()内积, 得

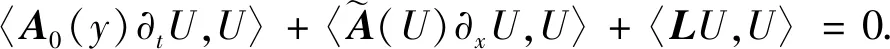
(14)

由表达式(8)～(10)通过简单计算, 易得

-2〈σ″(y)y∂xy,z〉+〈σ″(y)y∂ty,y〉.

(15)

由柯西-施瓦兹不等式及Sobolev空间嵌入定理(11), 将式(15)右边第一项化为

|〈σ″(y)y∂xy,z〉|≤C‖y‖L∞‖∂xy‖‖z‖≤

C‖y‖L∞(‖∂xy‖2+‖z‖2)≤

C‖U‖H2(‖∂xy‖2+‖z‖2)≤

由式(3)的第三个方程及分部积分, 式(15)右边第二项可化为

|〈σ″(y)y∂ty,y〉|=|〈σ″(y)y∂xz,y〉|=

|-2〈σ″(y)z∂xy,y〉-〈σ‴(y)yz∂xy,y〉|≤

从而得U的L2估计

(16)

一阶能量估计对式(5)关于x求一阶偏导数, 得

(17)

式(17)左乘矩阵A0(y), 并与∂xU作L2()内积, 得

2〈A0(y)(∂xA(U))∂xU,∂xU〉.

(18)

利用方程组(3), 并由Sobolev空间嵌入定理, 易得

|〈(∂tA0(y))∂xU,∂xU〉|=

|〈σ″(y)∂ty∂xy,∂xy〉|=

|〈σ″(y)∂xz∂xy,∂xy〉|≤

C‖∂xy‖L∞‖∂xy‖‖∂xz‖≤

(19)

|2〈-σ″(y)∂xy∂xz,∂xy〉|≤

C‖∂xy‖L∞‖∂xy‖‖∂xz‖≤

(20)

|-2〈A0(y)(∂xA(U))∂xU,∂xU〉|=

|2〈σ″(y)∂xy∂xy,∂xy〉|≤

C‖∂xy‖L∞‖∂xy‖2≤

(21)

将式(19)～(21)代入式(18), 得

(22)

二阶能量估计对式(5)关于x求二阶偏导数, 得

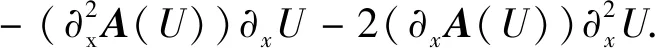
(23)

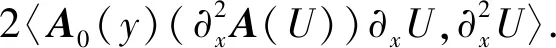
(24)

由表达式(7)～(10), 并由柯西不等式及Sobolev空间嵌入定理, 易得

(25)

(26)

(27)

(28)

将式(25)～(28)代入式(24), 得

(29)

最后, 将式(16),(22)和(29)相加, 得

(30)

从而得到式(13).

由式(13)知，要完成能量估计, 还需要给出‖∂xy‖H1,‖v‖H1,‖∂xu‖的时间耗散估计.

命题2对于任意的t∈[0,T], 成立

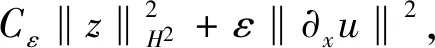
(31)

(32)

(33)

式中：ε为待定的正常数, 且与时间t无关.

证明首先证明式(31). 由式(3)中的第四个方程, 得

σ′(y)∂xy=∂tz-v+γz.

(34)

式(34)与∂xy作L2()内积, 由柯西-施瓦兹不等式和Young不等式, 得

〈∂xu,z〉+〈∂xz,∂xz〉+γ〈z,∂xy〉≤

Cε‖z‖2+ε‖∂xu‖2+‖∂xz‖2+

(35)

(36)

再证明式(32). 同样由式(3)中第四个方程, 得

v=∂tz-σ′(y)∂xy+γz.

(37)

式(37)与v作L2()内积, 得

〈∂x(σ(y)),v〉+γ〈z,v〉.

(38)

对式(38)右边的第四项进行分部积分, 得

-〈∂x(σ(y)),v〉=〈σ(y)-σ(0),∂xv〉=

(39)

其中

G(y)σ(y)-σ(0),

且有

成立, 当|y|≪1时.

将式(39)代入式(38), 由柯西-施瓦兹不等式和Young不等式, 得

γ〈z,v〉+〈σ″(y)z∂xy,u〉+〈(σ′(y)-1)z,∂xu〉≤

(40)

从而得

(41)

最后证明式(33). 式(3)第二个方程与∂xu作L2() 内积, 得

〈∂xu,∂xu〉=〈∂tv,∂xu〉+〈z,∂xu〉=

由柯西-施瓦兹不等式, 得

Cε‖z‖2+ε‖∂xu‖2.

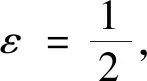
|∂xv‖2+C‖z‖2.

(42)

命题3对于任意的t∈[0,T], 成立

(43)

及

(44)

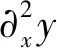
(45)

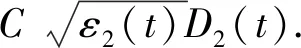
(46)

从而式(43)得证.

最后证明式(44). 对式(3)第四个方程关于x求偏导, 并与∂xv作L2()内积, 得

(47)

对式(47)右边的最后一项, 利用分部积分, 得

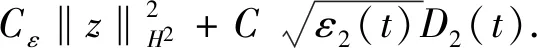
(48)

将式(48)代入式(47), 并利用Young不等式, 得

(49)

从而式(44)得证.

3 定理1的证明

将式(31)～(33)及(43)～(44)相加, 得

(50)

其中

B(t)=〈z,∂xy〉+〈u,y〉+4〈z,v〉+

〈∂xu,∂xy〉+4〈∂xz,∂xv〉+4〈∂x(σ(y)),∂xu〉.

从而有

(51)

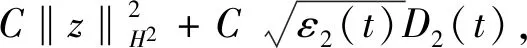
(52)

其中

对式(13)的两边同乘以C2并与式(52)相加, 得

(53)

取C2充分大, 使得γC2>C，则

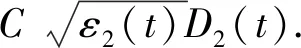
(54)

从而得

(55)

其中C3=min{γC2,C1}.

因为ε2(t)充分小, 由式(55)得

(56)

其中，C4为正常数, 对式(56)两端在[0,t]上积分,得

(57)

因为C2充分大, 故C2ε2(t)-B(t)与ε2(t)等价, 从而得

(58)

证毕.