基于字典学习与等效视数的低剂量CT伪影抑制算法

杨一鸣，刘 祎，桂志国

(中北大学 生物医学成像与影像大数据重点实验室，山西 太原 030051)

0 引 言

近年来，计算机断层扫描(Computed Tomography, CT)在肺癌检查中广泛应用，主要原因是CT在检测肺部小结节和早期肺癌中比胸部X-线检查更准确[1]. 数据显示，一次常规CT检查，受检者将受到剂量约为1.5～20 mSv的X射线辐射，且CT扫描引发的X射线辐射在所有放射检查产生的X射线辐射中比重较大，由于CT检查可能导致受检者余生患癌的风险加大，医学检测中已将重复CT扫描检查列为医源性辐射的主要辐射源[2]. 随着诊断技术的不断改进，限制辐射剂量的低剂量CT(low-dose computed tomography, LDCT)已被用于肺癌高危人群的常规筛查，但低剂量CT又会造成图像质量下降. 如何在扫描剂量尽可能低的条件下，获取与常规剂量扫描质量相同或者更利于医疗诊断的CT图像，自然就成为相关领域亟待研究的课题.

目前提高低剂量CT图像质量的方法可以分为三类：投影数据校正法，迭代重建法和后处理方法. 低剂量CT图像的后处理方法，是对已经获取的重建图像进行修正处理，这类方法不依赖于投影数据，即直接处理滤波反投影算法重建的CT图像，消除重建图像中的条形伪影和噪声. 后处理方法的难点是斑点噪声和条形伪影分布于整个CT图像上，不满足特定的噪声分布模型. 这种方法一般以标准剂量CT(Standard Dose Computed Tomography, SDCT)图像为参考标准，一方面要保证处理后的结果不能丢失原来低剂量CT图像中较小的组织结构，另一方面不能在处理的过程中引入新的噪声和伪影. 由于低剂量CT图像后处理效果的好坏直接影响医生诊断的准确性，国内外很多学者致力于对低剂量CT图像伪影和噪声抑制方面的研究. 最初，Rudin等[3]提出了总变分(Total Variation, TV)模型，TV去噪模型能够较好地保护图像边缘，但是该模型仅沿图像边缘的切线方向扩散，导致处理后的图像产生阶梯效应，后来，Zhu Yining等[4]提出一种改进的TV模型用于低剂量CT降噪，取得了不错的降噪效果； Zamyatin等[5]提出了一种自适应多尺度总变分低剂量CT图像滤波方法，在对低剂量CT图像伪影抑制的同时，较好地保护了腹部CT图像中组织结构的边缘； Liu Yi等[6]针对稀疏角度投影提出了基于中值先验约束的TV重建算法. 2005年，Buades等[7]首次提出了非局部均值(Non-Local Means, NLM)算法，该算法利用图像具有重复结构性质，在全局范围内搜索与像素点所在图像块相应的相似块，再对其进行加权平均来实现去噪. Chen Yang等[8]提出了利用结构相似信息的大尺度非局部均值滤波来处理腹部低剂量CT图像； Ha等[9]提出了通过小图像块数据库与局部相似性匹配相结合的方法，对低剂量CT图像后处理； 此外，Chen Yang等[10]提出了基于快速字典学习方法的腹部肿瘤低剂量CT图像伪影抑制算法.

字典学习和稀疏表示理论在图像处理领域的应用十分广泛，用于图像的去噪、 修复、 超分辨率重建[11]等方面. Aharon等[12]最早提出了K-奇异值分解(K-Singular Value Decomposition, K-SVD)算法，该算法利用逐列更新字典的方式，多次迭代建立了一个全局最优的过完备字典，通过字典的冗余性对图像进行稀疏表示； Chen Yang等[13]提出了一种基于区别性字典的条形伪影抑制方法，该方法首先使用小波变换分解低剂量CT图像，然后对水平、 垂直和对角方向的高频图像分别进行对应的区别性字典表达并去除伪影，最后再用传统的字典学习方法去除残留的噪声，取得了很好的效果. 受这种方法启发，本文提出了一种基于字典学习的伪影抑制算法，首先利用平稳小波变换(Stationary Wavelet Transform, SWT)对低剂量CT图像进行单层分解，并对三个方向的高频图像利用在线字典学习的方法训练字典，然后利用等效视数(Equivalent Number of Looks, ENL)对字典进行分区得到伪影字典和特征字典，并只对特征原子进行稀疏编码，经过小波逆变换(Inverse Stationary Wavelet Transform, ISWT)后，再采用双边滤波器(Bilateral Filter, BF)对处理后的CT图像进行分解并训练高频字典，最后通过等效视数摒弃伪影字典来去除高频图像残留的伪影和噪声，从而达到抑制条形伪影、 改善低剂量CT图像质量的目的. 将本文算法应用于实际的低剂量CT图像，与标准剂量CT图像相比较，并与TV降噪算法、 K-SVD算法和三维块匹配滤波(Block-Matching and 3-D Filtering, BM3D)算法[14]对比，本文算法的处理结果优于其他算法.

1 字典学习理论

1.1 稀疏表示

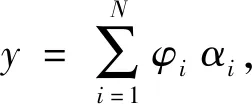
(1)

(2)

式中：‖α‖0为向量α的l0范数，表示α中的非零元素个数. 式(2)中允许y与Dα之间存在一定的误差ε，但是式(2)中的l0范数最小化问题在求解时是一个NP难题. 对于这种问题的求解方法，可以利用正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)求近似解.

1.2 正交匹配追踪算法

OMP算法[15]是在过完备字典中选择较少的列向量，形成一个对观测值的最优近似表示. 基于稀疏度限制L的稀疏表示问题可以描述为

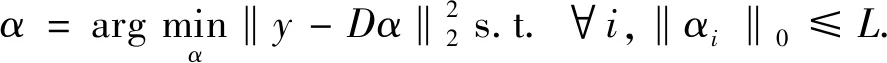
(3)

1.3 在线字典学习

1) 图像块处理：假设Pi是从一幅图像I中得到的第i个长度为p的图像块，将Pi表示成向量形式. 因此，训练集中第i个图像块可以分别表示为Ii=PiI.

2) 初始化训练参数：设定字典在训练阶段的正则化参数为λ，图像块集为Pn={P1,P2,…,Pn}，以Pn为输入信号.

3) 计算稀疏系数：由步骤(2)可知，迭代开始时D=D0，用最小角回归迭代方法求解，可使式(4) 的计算值最小.

(4)

式中：t表示训练字典的迭代次数，t={1,2,…,T}，根据输入的图像块向量Ii更新稀疏系数θt.

Dt

(5)

为了保证字典中的基向量值在一定的范围内，对求得的D加一个约束条件D∈c，归一化处理结果为

(6)

5) 最后生成字典：达到迭代次数T后，即可获得过完备字典DT.

2 本文算法

2.1 平稳小波变换

在经典的小波变换算法中，图像经过高通滤波和低通滤波后都要经过下采样，使分解后的各子带变为原图像大小的一半，但这样容易造成图像边缘的小波系数部分信息丢失，给重构图像带来不稳定性. 而平稳小波变换是对经典小波变换的改进，其最大的特点是冗余性和平移不变性. 本文算法中首先采用平稳小波变换对低剂量CT图像进行分解，通过平稳小波变换将LDCT图像分成低频和高频两部分，其中高频又包含了三个部分：水平高频部分，垂直高频部分和对角高频部分. 本文算法中使用哈尔(Haar)小波基进行分解，因其速度快且可以避免Gibbs振荡现象.

2.2 基于等效视数的字典分区方法

在对质量退化的低剂量CT图像I进行平稳小波变换(SWT)之后，将其分解成低频分量Ic a和三个高频分量：水平分量Ic hd、 垂直分量Ic vd和对角分量Ic dd； 然后把高频部分分别运用在线字典学习方法训练出三个方向上的字典Dc hd，Dcvd和Dc dd； 图 1 为构成字典的特征原子及伪影原子，均由水平分量字典随机抽取得到，相比特征原子图像块中的图像信息，伪影原子图像块中的图像信息变化更显混乱.

图 1 构成字典的原子Fig.1 Atoms from dictionary

(7)

(8)

(9)

图 2 三个方向高频分量的字典分区示意图Fig.2 Illustration of the dictionaries for the high frequency bands with different orientations

2.3 残留伪影的抑制

图 3 算法各步骤处理结果局部放大图Fig.3 Local amplified images of processing results by each step of the algorithm

本文算法的流程示意图见图 4，算法的具体步骤如下：

图 4 本文算法的流程示意图Fig.4 Flow schematic of the algorithm

Step 1：对低剂量CT图像I进行平稳小波变换，分解成低频分量Ic a与三个高频分量Ic hd,Icvd和Ic dd；

Step 2：设定字典训练阶段用到的正则化参数λ和图像块大小q，输入图像的图像块集Pn，初始字典D0，迭代次数T，利用式(4)进行字典训练，利用式(5)迭代更新字典；

Step 3：利用式(7)计算图像块的等效视数，将字典分区成伪影原子字典和特征原子字典；

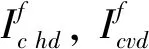
3 实验结果与分析

为了验证本文提出算法的有效性，采用实际的临床CT图像进行实验，CT图像由一台西门子SOMATOM Sensation 16排CT得到，图像大小为512×512. 其中LDCT图像由40 mAs电流扫描，SDCT图像由160 mAs电流扫描，重建算法为FBP. 选取如图5所示的两张LDCT图像进行测试，伪影抑制的结果与SDCT图像做对比，两组图都用腹窗显示(窗宽350 HU，窗位50 HU). LDCT图像选用B70f卷积核，SDCT图像则选用临床上腹部扫描和胸部扫描常用的B30f卷积核. 实现算法的工具为MATLAB R2014a，计算机的配置为CPU：Intel CoreTMi7-4771 QM CPU@3.50 GHz，内存8 192 Mb RAM. 本文算法中涉及到7个参数. 在线字典学习方法有4个参数，正规化参数λ取值为0.1，图像块的大小为16×16，字典训练块数量即为：(512-15)×(512-15)=247 009，字典中原子的个数为1 500，迭代的次数为90. 图像块的大小取为16×16，一方面有利于字典学习时提取图像的细节特征，另一方面有利于运用等效视数的方法区分伪影原子和特征原子. 运用分区的子字典稀疏表示时，所用OMP方法的稀疏限制水平参数L取为3. 双边滤波器中有3个参数，一个是滤波器的窗口的大小，通常设置为10×10，另外两个参数是空间标准差σd和密度标准差σr，在估计了几个可能的值后，发现σd=6，σr=0.2时能去除低剂量CT图像中的大部分的条形伪影.

图 5 测试图像Fig.5 Test images

图 6(c)～(f)给出了采用TV算法，K-SVD算法，BM3D算法处理结果以及本文算法对测试图a的结果对比，图6(a)和(b)分别为腹部LDCT图像和腹部SDCT图像. 图 7 给出了图 6 中各图对应的局部放大结果. 对比图7中(a1)和(b1)可以看出，相比于SDCT图像，LDCT图像中的伪影比较严重，解剖结构的细节分辨率低； 对比图 7 中(c1)和(b1)可以看出，TV算法虽然有效地去除了条形伪影，但是由于图像过度平滑造成细节信息损失； 对比图 7 中(d1)和(b1)可以看出，K-SVD算法去除了大量的噪声和伪影，但是图像有部分边缘变得模糊； 观察图 7 中(e1)可以看出，BM3D算法有效抑制了图像中的噪声和伪影，但是对比图 7 中(b1) 的部分细节发现BM3D算法处理后的图像过度平滑造成了边缘和细节信息的丢失. 从对比结果来看，本文的算法能有效地抑制伪影，在图像的边缘和细节保持方面优于其他算法，结果图与SDCT图像最为接近.

图 6 测试图a的各种算法处理后结果图Fig.6 Various algorithms processed result images of test image a

图 7 中的(a2)～(f2) 给出了图 6 中各图对应的肝脏肿瘤部分局部放大结果，图 7 中(a2)中箭头所指为肝脏肿瘤部分. 对比图 7 中(a2)和(b2)可以看出，相比SDCT图像中的肿瘤部分，LDCT图像难以找到准确的肿瘤部分，噪声影响比较严重； 对比图 7 中(c2), (d2), (e2)和(f2)可以看出，图 7 中(f2)与SDCT图像的肿瘤部分最接近，效果最好.

图 7 测试图a结果图对应的局部放大结果Fig.7 Partial magnification of result images of the test image a

图 8 给出了测试图b的各种算法处理结果图，图8(a)～(f)分别是LDCT图像、 SDCT图像、 TV算法处理结果、 K-SVD算法处理结果、 BM3D算法处理结果和本文算法处理结果图.

图 9 给出了图 8 中各图对应的局部放大结果. 对比图9(c)和(b)，TV算法会由于图像过度平滑造成细节信息损失； 对比图9(d)和(b)可以看出K-SVD算法去除了大量的噪声和伪影，但是图像还是存在部分边缘模糊的情况； 由图9(e)可以看出，BM3D算法有效抑制了图像中的噪声和伪影，但是与图9(d)对比会发现BM3D算法处理后的图像细节部分比较好. 而本文的算法在抑制噪声和伪影的同时有效地保持了组织结构分辨度，展现出了真实SDCT图像的纹理部分. 处理后的测试图b 中组织部分保留的细节纹理较多且清晰，因此从视觉效果来看，本文算法的处理结果相比其他算法最好.

图 8 测试图b的各种算法处理后结果图 Fig.8 Various algorithms processed result images of test image b

图 9 测试图b结果图对应的局部放大结果Fig.9 Partial magnification of result images of the test image b

为了对算法结果进行客观、 定量的评价，本文采用较常用的峰值信噪比、 均方根误差和结构相似性来评价处理后CT图像的质量. 这些参数的定义如下：

1) 峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)

式中：M×N表示图像的大小；v是SDCT图像；u是伪影抑制后的图像. PSNR是图像信噪比变化情况的统计平均，其值越大，图像失真越少，这里取Peak=255.

2) 均方根误差(Root Mean Square Error, RMSE)

(12)

均方根误差是用来衡量u与u0之间的偏差，其值越小，图像u失真越小.

3) 结构相似性(Structural Similarity Index Measurement, SSIM)

SSIM(v,u)=[L(v,u)]α×[C(v,u)]β×

[S(v,u)]γ，

(13)

(14)

(15)

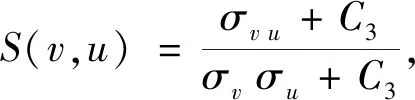
(16)

表 1 和表 2 分别给出了不同算法对测试图a和测试图b处理后的质量评估参数，表 1 和表 2 由图 10 分别截取SDCT图像的感兴趣区域(Region of Interest, ROI)计算得到，每张测试图像分别截取两个感兴趣区域.

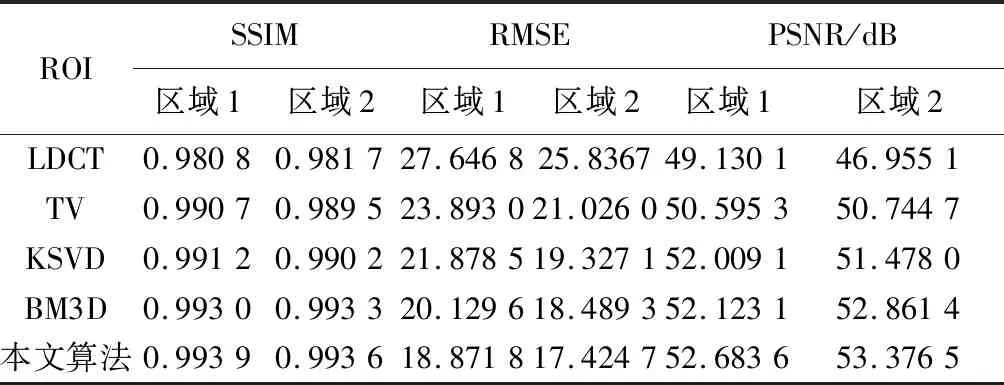
表 1 测试图a的质量评估参数

表 2 测试图b的质量评估参数

由表 1 和表 2 分析可知：本文提出算法与其他算法相比，结构相似性SSIM和峰值信噪比PSNR都较大，均方根误差RMSE较小. 说明本算法处理后的图像质量较好，能够有效地抑制伪影，并保留图像的边缘等重要细节特征. 因此，在视觉效果和定量评价方面，所得结果都表明本文提出的算法对低剂量CT图像的伪影抑制是有效的.

表 3 给出了不同算法对测试图a和测试图b处理后的运行时间，可以看出，本文所提算法的计算速度优于K-SVD算法，但是相比于BM3D算法，运行时间还是相对较长，对算法加速方面而言，可作为下一步研究的方向.

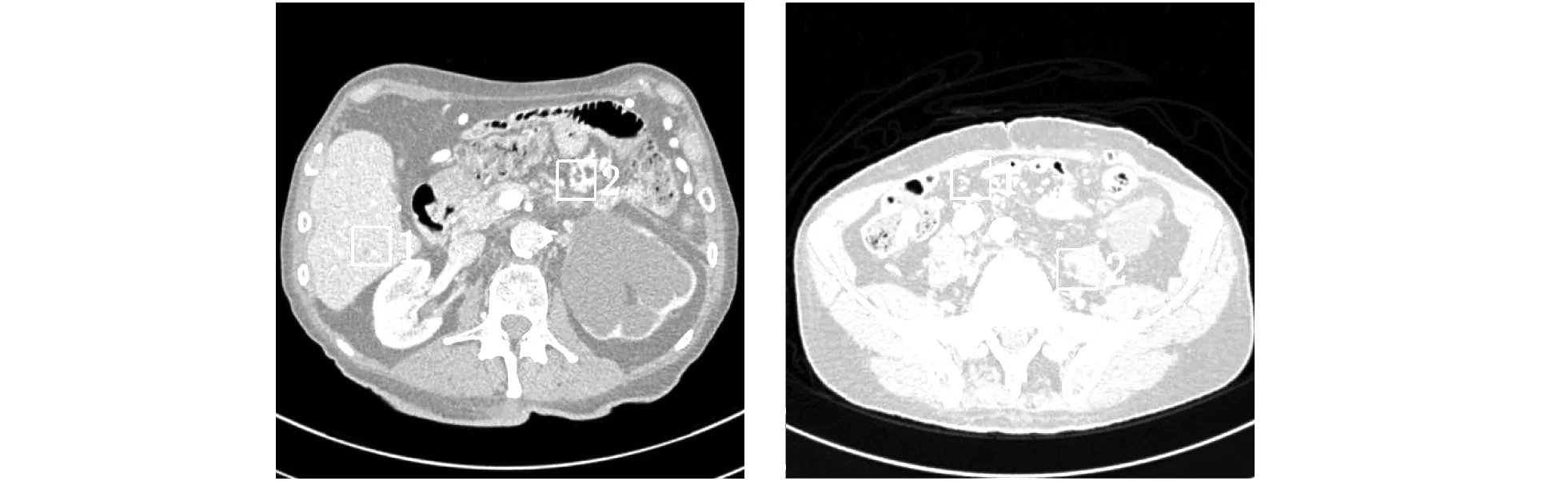
图 10 选取SDCT图像的感兴趣区域Fig.10 Select the region of interest of the SDCT image

4 结 论

本文提出了一种基于字典学习与等效视数的伪影抑制算法，利用FBP算法获得低剂量CT重建图像，再对CT图像进行降噪处理. 本文算法在处理低剂量CT图像的过程中，每一步骤得到的高频分量都运用字典学习方法训练得到字典，再运用等效视数判别法对字典进行分区得到伪影字典和特征字典，并只对特征原子进行稀疏编码，从而达到去除条形伪影的目的. 实验结果表明，本文算法可以在抑制条形伪影的同时，保留较多的细节信息，并且更加接近原始SDCT图像. 从视觉效果和质量评价可以看出，本文算法的伪影抑制效果优于TV算法、 K-SVD算法和BM3D算法. 但是，本文所提算法中一些参数的选择，仍需凭借经验调整，这也是后续研究中需要解决的一个问题.