基于支持向量回归的锂电池健康状态估计
2019-11-22张新锋饶勇翔姚蒙蒙
张新锋,饶勇翔,姚蒙蒙
(1. 长安大学汽车运输安全保障技术交通行业重点实验室,陕西 西安 710064;2. 长安大学 汽车学院,陕西 西安 710064)
0 引 言
锂离子电池因其具有单体电池电压高,循环寿命长,安全性能好、 自放电效应小的优点成为现在电动汽车的主流动力装置. 为了保证电动汽车运行的安全性和经济性,必须要对锂电池进行管理研究,锂电池健康状态(SOH)估计是锂电池管理的核心. 掌握锂电池健康状况有利于替换老化的电池,提高整体电池组的使用寿命,因此,准确实现电池的健康状态估计有重要实际意义.
实际应用过程中锂电池的健康状态无法直接测量,只能通过估计得到. 由于电池老化知识的缺乏,准确的健康状态估计成为很大挑战. 康燕琼[1]以单体电池等效电路为基础,建立了电池组的二阶RC电路模型,以实时采集到的出租车充电数据对模型参数进行辨识求解,然后将粒子滤波和等效电路模型相结合,利用实测数据实现了内阻的准确估计,但是对于内阻和SOH之间的具体关系没有确定. Bhaskar Saha等[2]经过多年的研究,证明电池容量退化量与交流阻抗存在线性关系,该方法能够准确描述阻抗的变化,但是不能用于在线实施,需要专业仪器,测量过程复杂. 叶婧[3]通过获取放电的电压、 容量数据,建立了高斯回归模型,将基于组合核函数的高斯过程回归算法应用于锂电池容量数据的离线建模,结果表明,该算法能对电池健康状态进行准确估计. 但是该方法只考虑了电池恒流恒温放电的情况,难以适用于电动汽车复杂运行工况下锂电池的健康估计.
数据驱动方法不需要考虑电池充放电的电化学反应和失效机制,直接从试验数据和监测数据中挖掘隐含的健康状态信息. 基于此,本文在考虑电动汽车复杂工况的情况下,利用充放电可监测参数提取健康因子,采用支持向量回归(SVR)建立健康状态估计模型,实现SOH估计. 最后对模型的精度进行了验证,分析结果验证了该方法的有效性.
1 SOH定义及健康因子的构建
电池健康状态表征锂电池相对于新电池储存电量的能力,是定量描述电池退化程度的指标,表征健康状态的指标有容量、 功率、 阻抗等. 电池容量的衰减是电池健康状态的重要表征,因此,本文选择电池容量来定义电池的健康状态,SOH的定义表达式[4]为

(1)
式中:Caged为当前电池容量;Crated为电池的额定容量;Cold为电池寿命终止容量. 其中,电池的容量为锂电池在室温条件下,以1C的放电电流放电到截止电压所释放的最大电量.
通过式(1)对SOH进行估计,需要了解当前状态下的电池容量,然而在实际运行中电池的容量难以直接测量,因此需要新的估计方法估算电池容量. 此外,容量会随温度、 负载等条件不断变化,所以对锂离子电池的容量估计具有很大的难度. 利用电池的外特性数据进行电池容量估计,认为电池的充放电数据信息反映了电池的内部特征,从中提取参数表征电池的健康状态. 而且电池的特性数据获取较为容易,具有更高的实用性,这些能够表征电池容量的外特性参数被定义为健康因子.
电池的电压/电流信息能够反映电池的健康状态信息,且在工作时比较容易获得. 但是,电压会受到温度、 SOC的影响,考虑在运行时采集锂电池的运行数据,把影响电压的温度、 荷电状态(SOC)等因素也加以考虑. 将电流、 电压、 温度、 SOC融合成健康向量作为健康因子,并将其作为支持向量回归的输入,将电池的当前容量作为输出,训练SOH估计模型[5],进而实现动态工况下的锂电池健康状态估计.
2 支持向量回归估算SOH的方法
支持向量机[6](SVM)是统计学习理论VC维理论和结构风险最小原理的具体实现. SVM方法用少量的支持向量代表整个样本集,在模型的复杂度和学习能力之间寻求最佳平衡,以获得最佳的推广能力. SVM擅长处理样本数据线性不可分的情况,主要通过惩罚函数和核函数技术实现. 目前,SVM算法在模式识别、 回归估计、 概率密度函数估计等方面都有应用.
2.1 支持向量回归模型构建
假设有n个训练样本数据(xi,zi),其中xi为第i个输入样本,zi为对应的输出值. 考虑线性回归的函数表达式为
f(x)=(ω·x)+b,ω∈Rn,b∈R.
(2)
在数值计算中,允许f(x)与真实值z之间存在一定的误差,需要引入合适的损失函数.
|f(xi)-zi|≤ξ*+ε.
(3)
基于结构风险最小化原则,得到支持向量回归算法,把回归问题转化成在约束条件下的最优问题,其形式为[7]
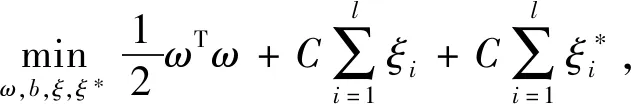
(4)
ωTφ(xi)+b-zi≤ε+ξi,
(5)

(6)

(7)
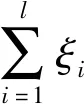

(8)
eT(α-α*)=0.
(9)
最终得到的回归函数为
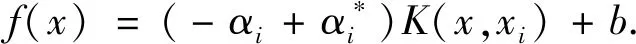
(10)
对电池的分析可知,锂电池的健康状态估计模型是一个有关监测参数的多元非线性模型,描述成数学模型为
C=f(i,v,T,SOC),
(11)
式中:i为电池的放电电流;v是电池的端电压;T为电池温度;SOC为电池的荷电状态;C为当前健康状态电池容量.
对于非线性回归模型,支持向量回归机的基本思想是利用内积函数将训练数据映射到一个高维空间,在高维空间中运用函数进行线性回归,然后返回到原空间,得到原输入空间的线性分类[8]. 这个内积函数称为核函数.
在模型的训练过程中,核函数是决定支持向量机性能的关键因素. 本文选用的高斯径向基核函数[9]是应用最广泛的核函数,识别率高,性能较好,在训练集减少的情况下性能未发生退化. 径向基核函数的表达式为
K(x,xi)=exp(-γ‖x-xi‖2),γ>0.
(12)
2.2 SOH估计流程
支持向量机估算SOH主要分为支持向量回归机模型训练和SOH估计两部分.
1) 支持向量回归机模型训练:对电池进行动态工况下的老化试验,监测记录运行参数,提取健康因子. 每隔一段时间,对电池进行容量标定. 以电压、 电流、 温度和SOC为输入,以容量为输出,建立支持向量回归机模型.
2) 锂电池SOH估计:基于电池运行数据提取健康因子,输入到支持向量回归机模型,估计当前锂电池容量. SOH的计算由定义式(1)得到.
SOH预测方法流程如图 1 所示.
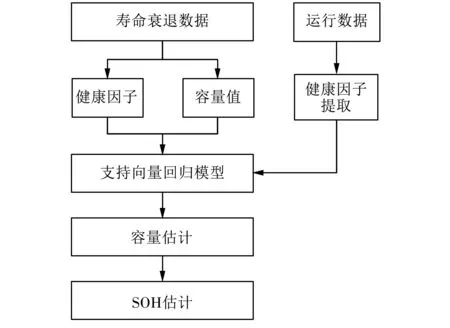
图 1 SOH预测流程Fig.1 SOH prediction process
3 数据来源与预处理
以型号为18650的电池为研究对象,研究锂电池在动态工况下,不同温度的电池容量衰减情况,并自动监测记录动态工况下的电流、 电压、 温度等状态参数. 每隔一段时间,对锂电池进行一次电池容量的标定,作为当前的锂电池最大可充容量值,以研究锂电池容量和其健康因子之间的内在联系.
本文的数据来源于NASA的实验室[10],试验采用的电池为18650号电池,其基本的参数信息如表 1 所示. 四个编号分别为RW9,RW10,RW11,RW12的锂电池在-4.5~4.5 A的电流之间进行随机充放电,并采集电池的充放电信息,采集的信息包括电流、 电压以及温度值等,采样间隔为1 s,每5 min改变一次电流值,在进行大概1 500次电流变化(大约5 d)后,对锂离子电池进行一次参考充放电循环.

表 1 电池基本参数
锂电池的容量标定过程如下:
1) 锂电池在室温条件下,恒流2 A充电至4.2 V,再恒压充电至电流降到0.01 A.
2) 以2 A的电流放电到截止电压3.2 V.
3) 重复以上过程两次,取两次放电容量的均值作为当前的容量值.
本文采用RW9号电池的充放电数据,在电池容量衰退到73%时,视为寿命终止. 全新电池的实际容量为2.096 2 Ah, 寿命终止时容量为1.523 1 Ah. 锂电池放电到寿命终止进行了10次的参考容量标定,将每两次容量标定之间的充放电过程作为一个周期. 由于两个参考点之间的时间间隔为5 d,近似认为容量标定后的两个小时放电时间内容量不发生衰退. 在每次容量标定后的两个小时内随机选取1 000个样本点作为训练样本, 即有 10 000 个训练样本参与支持向量回归机模型的训练,每个样本点包含五维参数信息,用来验证健康因子与容量之间的相关性. 图 2,图 3 为选取的训练样本的电流电压数据. 表 2 为部分样本数据信息.
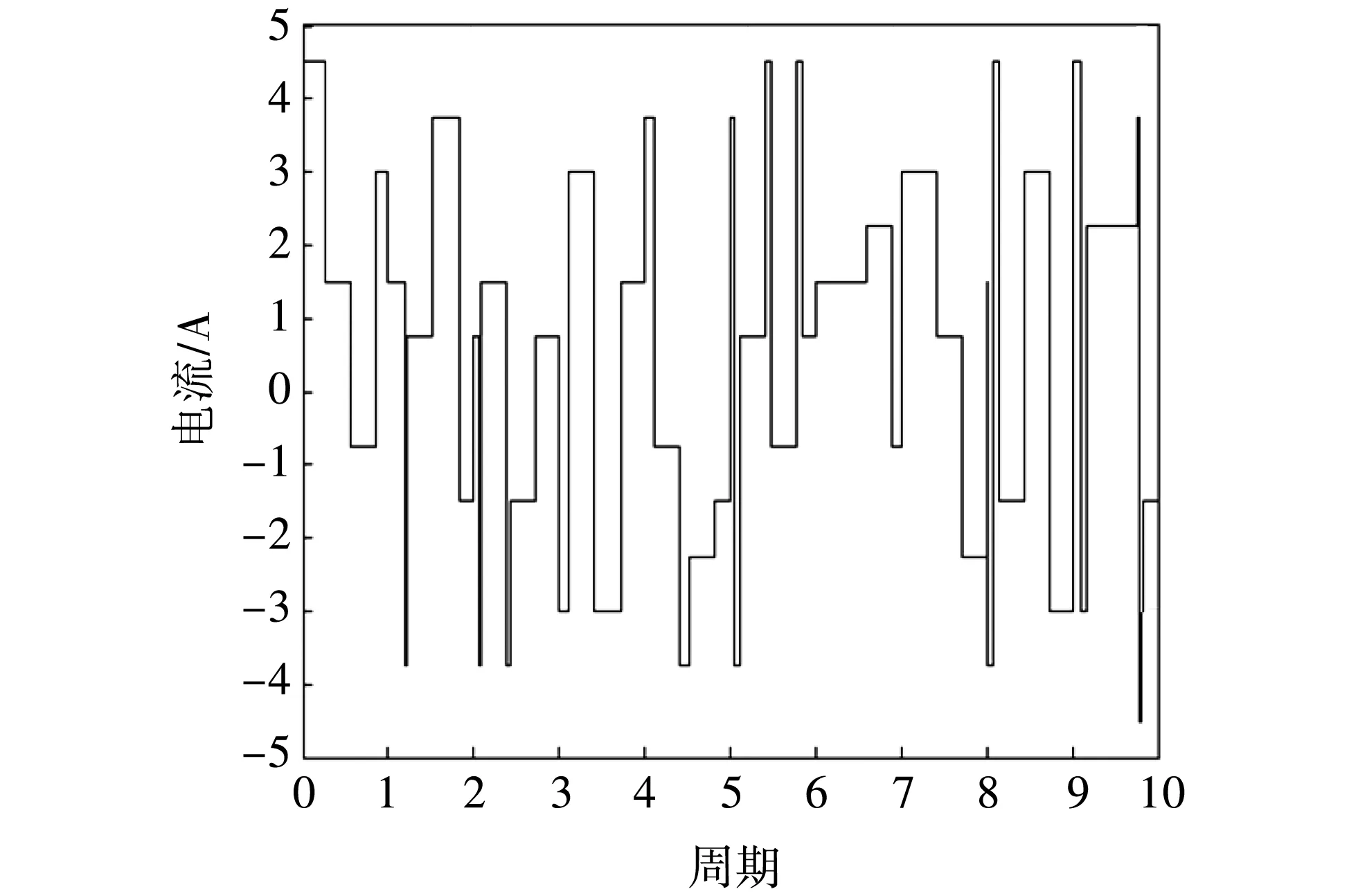
图 2 样本电流数据Fig.2 Sample current data

图 3 样本电压数据Fig.3 Sample voltage data
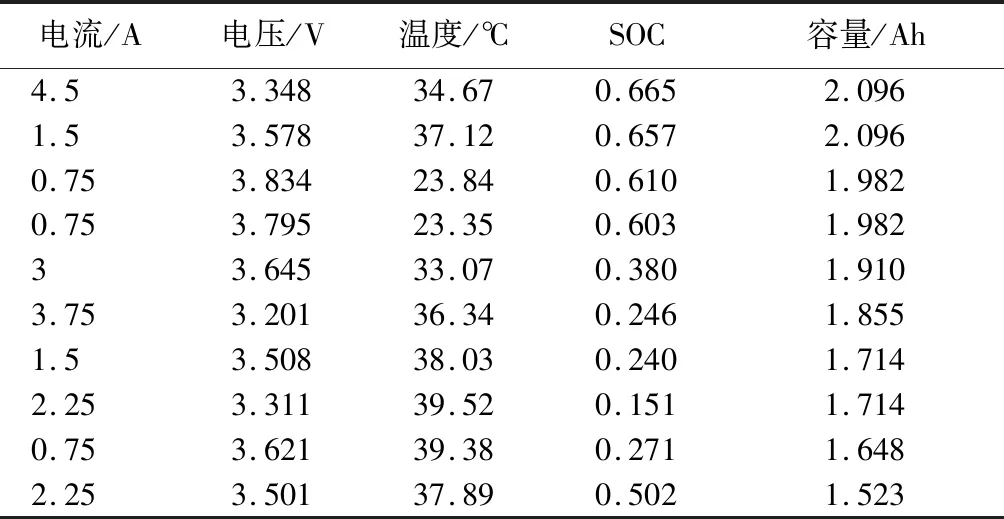
电流/A电压/V温度/℃SOC容量/Ah4.53.34834.670.6652.0961.53.57837.120.6572.0960.753.83423.840.6101.9820.753.79523.350.6031.98233.64533.070.3801.9103.753.20136.340.2461.8551.53.50838.030.2401.7142.253.31139.520.1511.7140.753.62139.380.2711.6482.253.50137.890.5021.523
4 健康状态估计模型与结果分析
4.1 模型参数寻优
支持向量回归在应用时有着独特的优势,但是在应用过程中一个比较重要的问题是必须确定合适的参数值,只有确定良好的参数值,才能使支持向量回归机模型获得更好的效果. 不同的待定参数对模型的影响非常大,如果参数值选择不合理,则会导致模型的过拟合或者是欠拟合,最终影响估计结果.
在建立SVR模型时,需要选择的参数包括惩罚系数C,还有核参数g[11].C表示对经验误差的惩罚,在置信风险和经验误差之间起折中的作用,当C的值取得较小时,对经验误差的惩罚小,致使不能通过样本的学习获得小的拟合与预测误差; 当C的值取很大时,对经验误差的惩罚较大,导致过学习,泛化推广能力下降,预测误差较大. 核函数参数值也会影响模型的预测性能,对于特定问题,参数取值应该在一定的区间内.
网格搜索是一种详尽的参数搜索方法,相对于近似搜索等方法具有更高的可靠度. 由于本例中的待搜索参数只有两个,其搜索的时间复杂度并不大. 并且每对的(C,g)相互独立,网格算法更便于实现算法并行化计算. 基于V折交叉验证的网格搜索法,在搜索得到最优参数的同时,也有降低模型泛化误差,防止模型过拟合的作用,最终提升了模型对于未知数据的预测能力.
本文采用网格搜索法,将实验数据分为5个大小相等的子集,用4个子集作为训练集,剩下一个数据集做预测. 循环这个过程直至每个子集都被预测一次,选择MSE最低的一对参数对作为最优化参数对. 基于网格搜索得到的最佳参数估计值如图 4 所示. 由图 4 可知,最优参数:C=256,g=0.329 88,CVMSE=0.004 818 7.
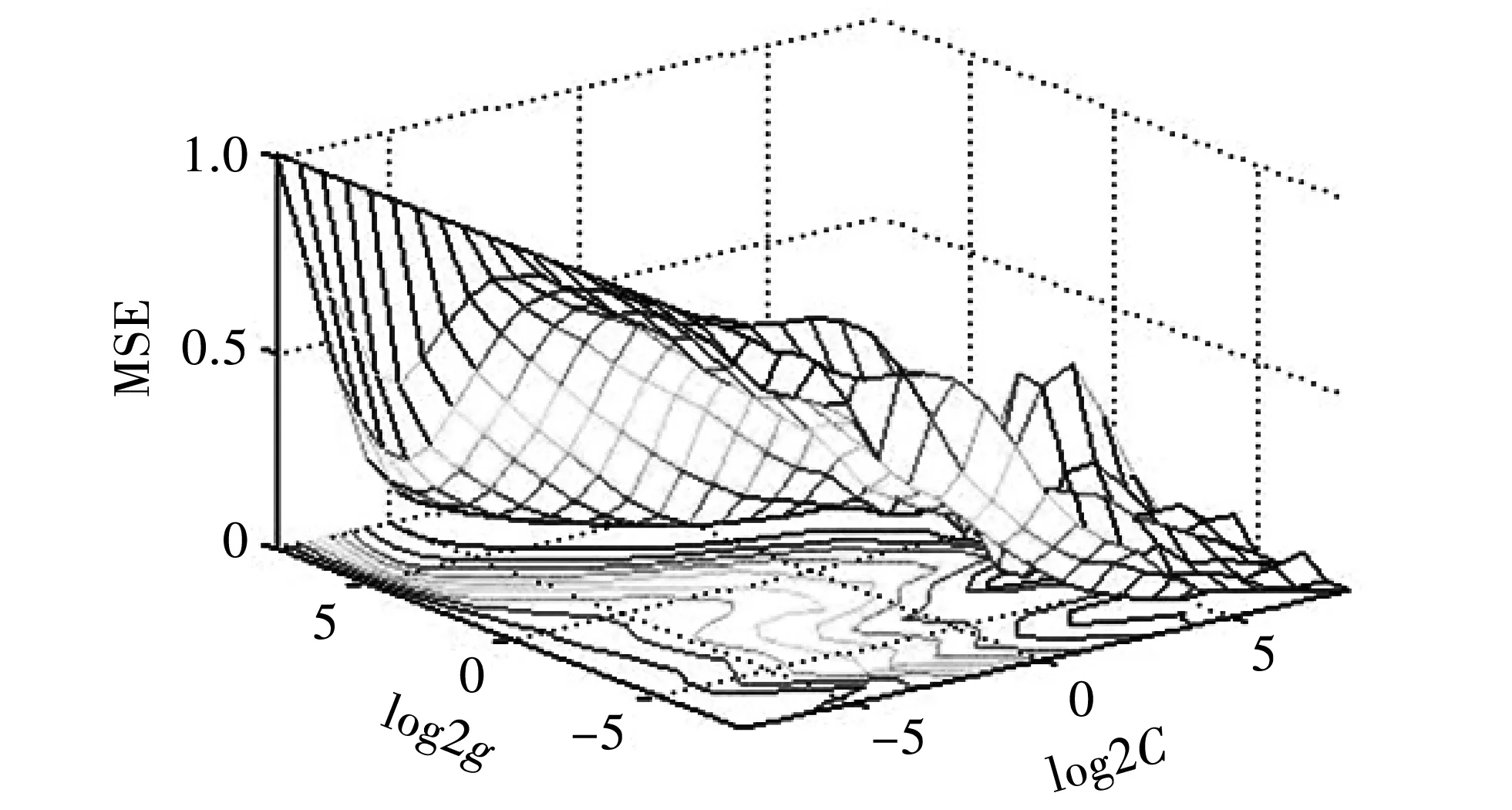
图 4 SVR参数优化结果Fig.4 Results of parameter optimization for SVR
4.2 SOH估计模型训练
为了评估电流、 电压、 温度、 SOC作为健康因子的合理性和有效性. 建立支持向量回归机模型评估电流、 电压、 温度、 SOC和容量之间的相关性.
根据4.1节获取的样本数据,对数据进行处理,使之满足模型训练的格式. 模型的输入为[V,i,T,SOC],模型的输出为容量,根据网格搜索算法获得的最佳参数值(C取值为256,g取值为0.329 88),训练支持向量回归机模型. 将健康因子输入到模型中,得到容量的估计值,模型的容量估计值与真实值得对比如图 5 所示.
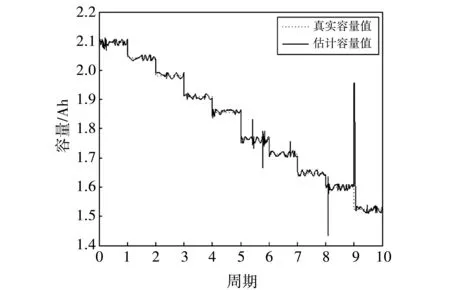
图 5 容量回归估计结果对比Fig.5 Comparison of capacity regression estimation results
从结果图中可以看到,将提取的健康因子输入到模型中,得到的结果和其真实值相比,除个别离群点外,整体的拟合效果良好,两者的平方相关系数为0.983 4,均方误差为0.000 57. 表明了选取的健康因子能够有效地表征电池的健康状况.
4.3 锂电池容量估计
验证模型的泛化能力,选择样本训练之外的200 s放电数据的样本对模型进行验证,样本的放电时间间隔为1 s,放电样本的当前容量参考值为1.762 3 Ah,将健康因子输入到模型之中,将预测结果与容量的参考值进行对比. 为了体现支持向量回归对电池容量预测的可靠性和优越性,使用BP神经网络对样本数据进行训练,将得到的估计容量与支持向量回归机的估计容量对比,结果如图 6 所示,图 7 为两种方法的估计误差对比.
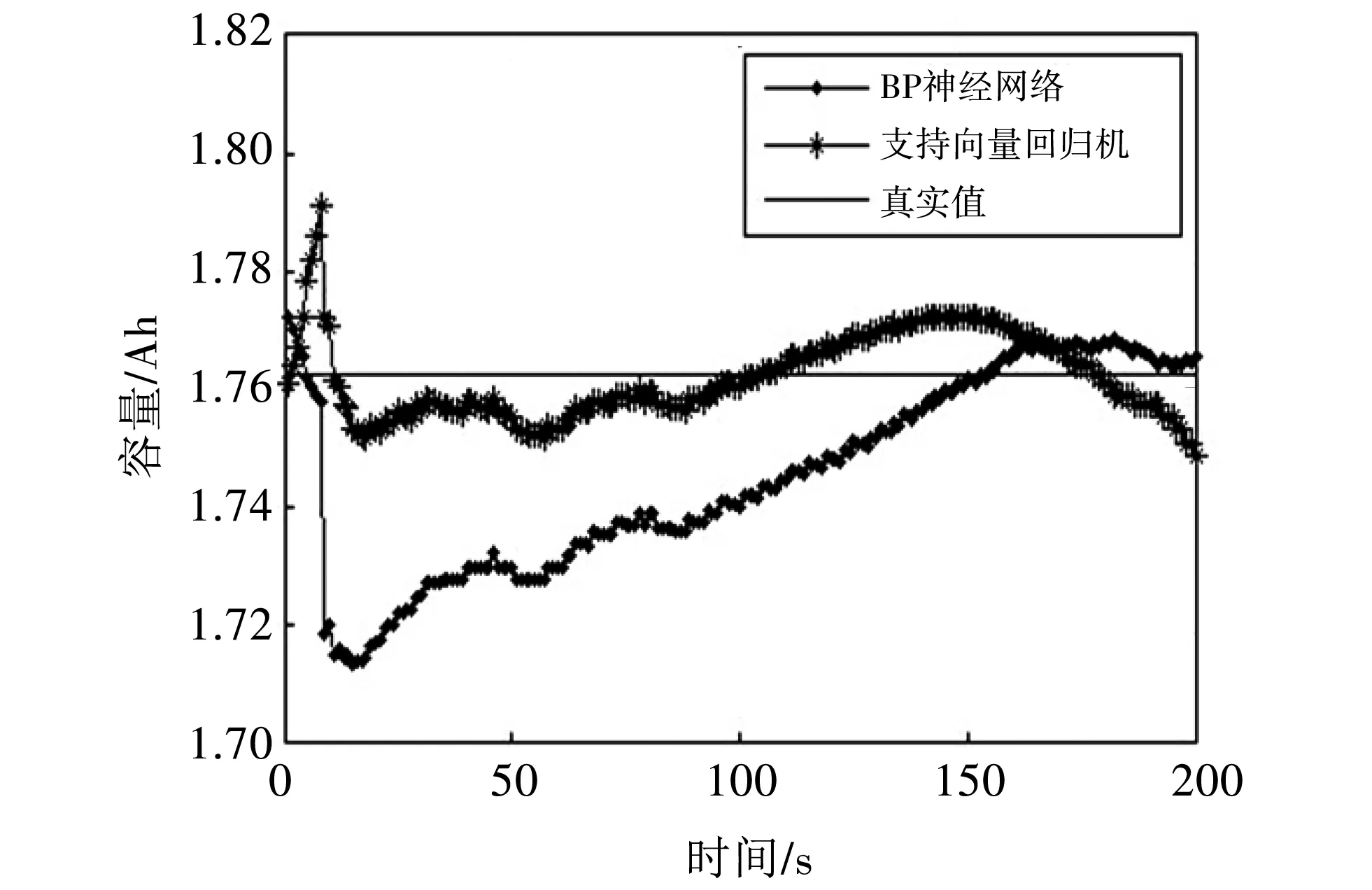
图 6 容量的估计结果对比Fig.6 Comparison of capacity estimation results

图 7 容量估计误差对比Fig.7 Comparison of capacity estimation errors
由图 6,图 7 可知,将锂电池运行数据输入到模型中,容量的估计结果接近真实值,且误差的波动较小,最大的容量估计误差1.64%. 支持向量回归机相对于BP神经网络有更高的估计精度.
4.4 锂电池SOH估计
将获得的容量估计值,结合SOH的定义可以获得SOH的估计值,如图 8 所示,为支持向量回归机模型与BP神经网络模型对电池SOH的估计结果,图 9 为两种方法SOH估计误差的对比.
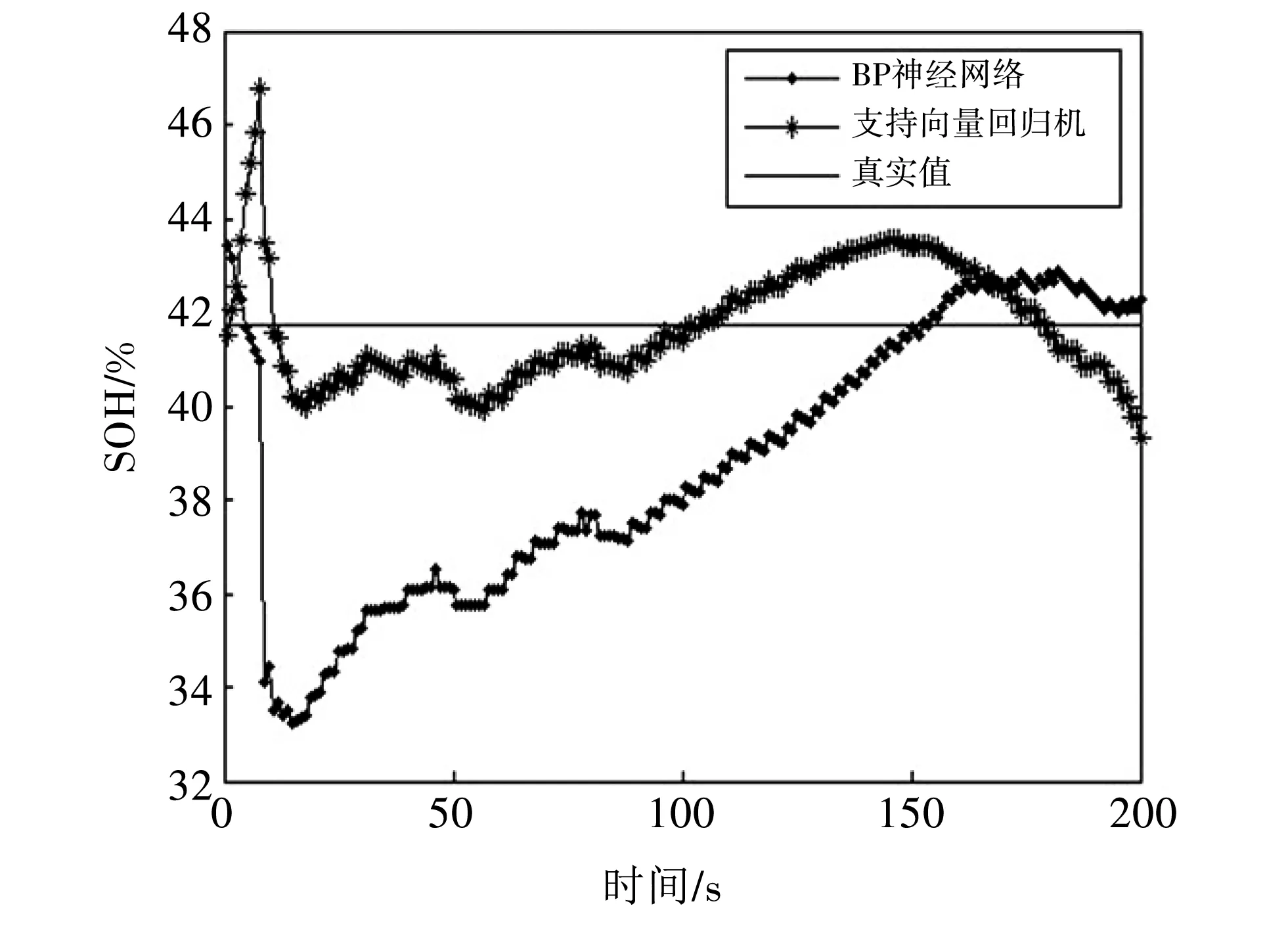
图 8 SOH估计结果对比Fig.8 Comparison of SOH estimation results
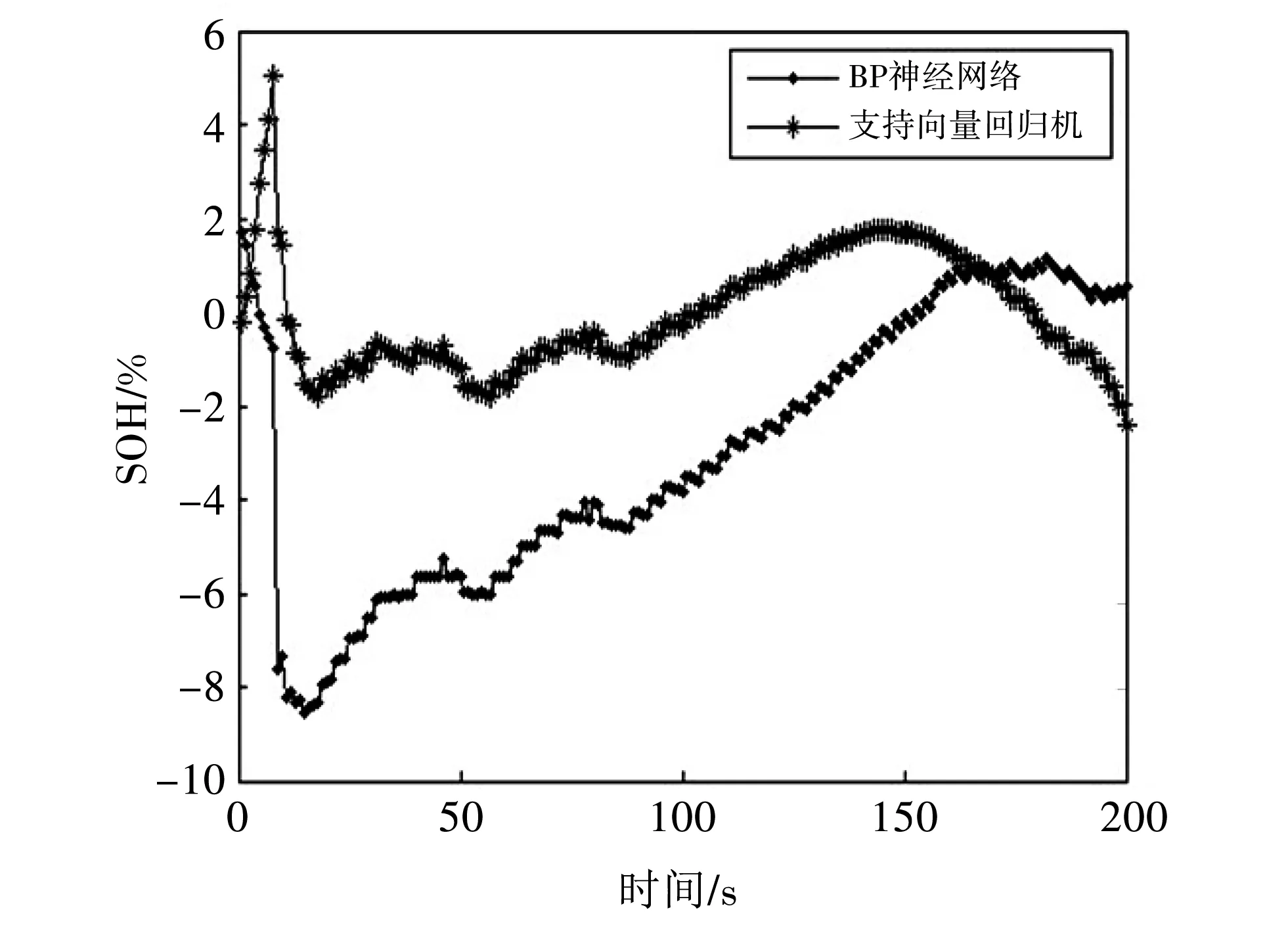
图 9 SOH估计误差对比Fig.9 Comparison of SOH estimation errors
从图 8,图 9 可以看出,用200 s的放电时间监测数据对锂电池进行健康状态估计,在电流,温度变化的情况下,健康状态的估计值在真实值附近波动,支持向量回归模型的误差及其波动更小. 两者的误差对比如表 3 所示.
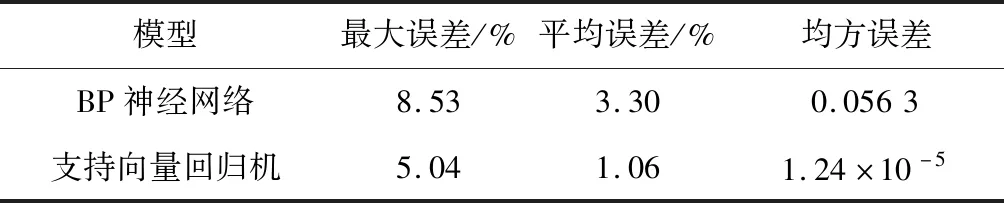
表 3 两种估算方法误差统计
由表 3 可知,基于动态工况运行数据对锂电池进行健康状态估计是可行的. 在200s的放电时间,SOH的估计结果最大误差为5.04%,平均误差只有1.06%. 在实验数据有限的情况下,采用支持向量回归机相对于BP神经网络有更高的估计精度. 提取多个健康状态下的200 s运行数据的健康因子,输入到支持向量回归模型中,取200 s的估计平均值作为SOH的估计值,与真实值的对比如表 4 所示.
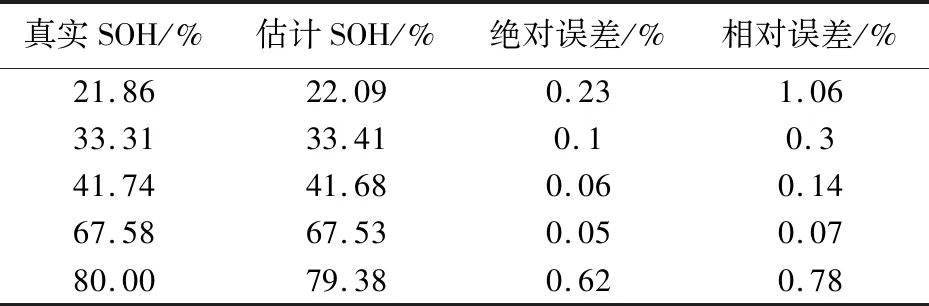
表 4 SOH估计结果
表 4 显示了电池健康状态估计的相关结果. 由表可见,基于本文提出的新的健康因子,采用支持向量回归的方法对动态工况下的SOH估计取得了较好的估计效果,SOH的估计误差总体上小于1%.
5 结 论
本文提出的动态运行工况下的锂电池健康状态估计方法,以电压、 电流、 温度、 SOC作为健康因子,可以实现运行过程中各种工况的健康状态的准确估计,克服了传统循环寿命法、 内阻法等实用性差的缺点.
利用支持向量回归机构建健康状态估计模型,在数据较少的情况下,能充分利用小样本数据的特性,使用网格搜索算法获得最优参数对,有效地防止了模型过拟合,降低了泛化误差,提高了模型的估计能力.
