基于改进的遗传算法与人工神经网络的类流感的预测
2019-11-22胡红萍白黄琴白艳萍张菊平刘茂省
胡红萍, 白黄琴,白艳萍,张菊平,刘茂省
(1. 中北大学 理学院,山西太原 030051; 2. 山西大学 复杂系统研究中心,山西 太原 030006)
0 引 言
流感是影响健康的多种因素之一,它可能导致严重的疾病和死亡,尤其是类流感(ILI)疾病,它对公众健康有着至关重要的影响. 当一个人的体温在100华氏度(37.8 ℃)或更高时,发烧、咳嗽和/或喉咙痛,除了流感之外,没有其他已知原因,根据美国疾病预防控制中心(CDC)和世界卫生组织组织(WHO)的定义,他或她诊断得了类流感(ILI)疾病[1]. 而疾病检测和监测系统提供了准确的实时监测、早期检测、流感爆发预测,这有助于卫生官员制定预防措施和协助诊所医院管理人员[2].
模拟达尔文进化论的遗传算法(GA)[3]和模拟鸟类行为的粒子群优化算法(PSO)[4]分别在1992年和1995年被提出. 自此以后,人们提出了许多智能算法,例如:正弦余弦算法(SCA)[5], 蚁狮算子(ALO)[6-7], 鲸优化算法(WOA)[8], 飞蛾扑火优化算法(MFO)[9], 入侵性杂草优化(IWO)[10]. 这些智能算法不断地改进并应用于各个领域. 例如:GA不断地被改进并应用于银行贷款决策[11]、 易腐产品[12]、 车辆路径问题[13]和混凝土拱桥[14]等; IWO与其他智能算法结合在一起实现性能改进,诸如基于混沌理论改进的IWO应用于PID控制器[15], 基于差分进化(DE)和IWO 的混合算法实现函数优化[16]. 另外,人工神经网络是目前有效的预测方法之一,并且群智能算法被用来优化人工神经网络的参数. 例如:PSO被用来优化径向基神经网络的参数实现AQI预测[17]; GA被用来优化BP神经网络的参数从而实现股票预测[18].
本文将GA和IWO组合形成一个新颖的混合算法,记为IWOGA,并将IWOGA应用于优化BP神经网络的权值和偏差,建立了新的模型IWOGA-BPNN. 并将此模型用于预测未加权的%ILI.
1 基本算法
1.1 遗传算法
1992年,Holland提出了模拟达尔文进化论的遗传算法(GA)[3]. GA模拟了生命进化机制,即自然选择和遗传进化中的繁殖、交配和突变. 在GA中, 最优解是通过任意初始化种群,三个算子,繁殖和进化得到的.
1.1.1 染色体表达式
实际问题的每一个可行解都由具有基因类型的结构化字符串数据表示. 而结构化字符串数据的不同组合构成了不同的可行解. 染色体表示有三种常用方法:二进制编码、符号编码和浮点编码.
1.1.2 初始化种群
任意产生N个初始的结构化字符串数据,其中每个结构化字符串数据是一个个体. 这样,种群由N个个体组成.
1.1.3 适应度值
根据实际问题,确定每个个体的适应度函数,并计算每个个体的适应度值. 在整个GA中,适应度函数是必不可少的部分.
1.1.4 遗传算子
在GA中, 有三类遗传算子:选择,交叉和变异.
1) 选择. 选择算子是根据一定规则从目前种群中选择部分个体作为下一代种群的个体. 常用的选择算子包括:轮盘赌选择方法、 排序选择法与最优保存策略.
2) 交叉. 交叉算子模拟遗传重组过程,以便将当前的最佳基因转移到下一个群体中并获得新的个体. 交叉算子的具体步骤如下:
步骤1: 在种群中任意选择一对个体;
步骤2: 根据个体的长度,随机选择一个整数或多个整数作为交叉位置.
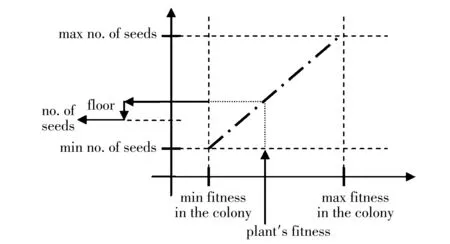
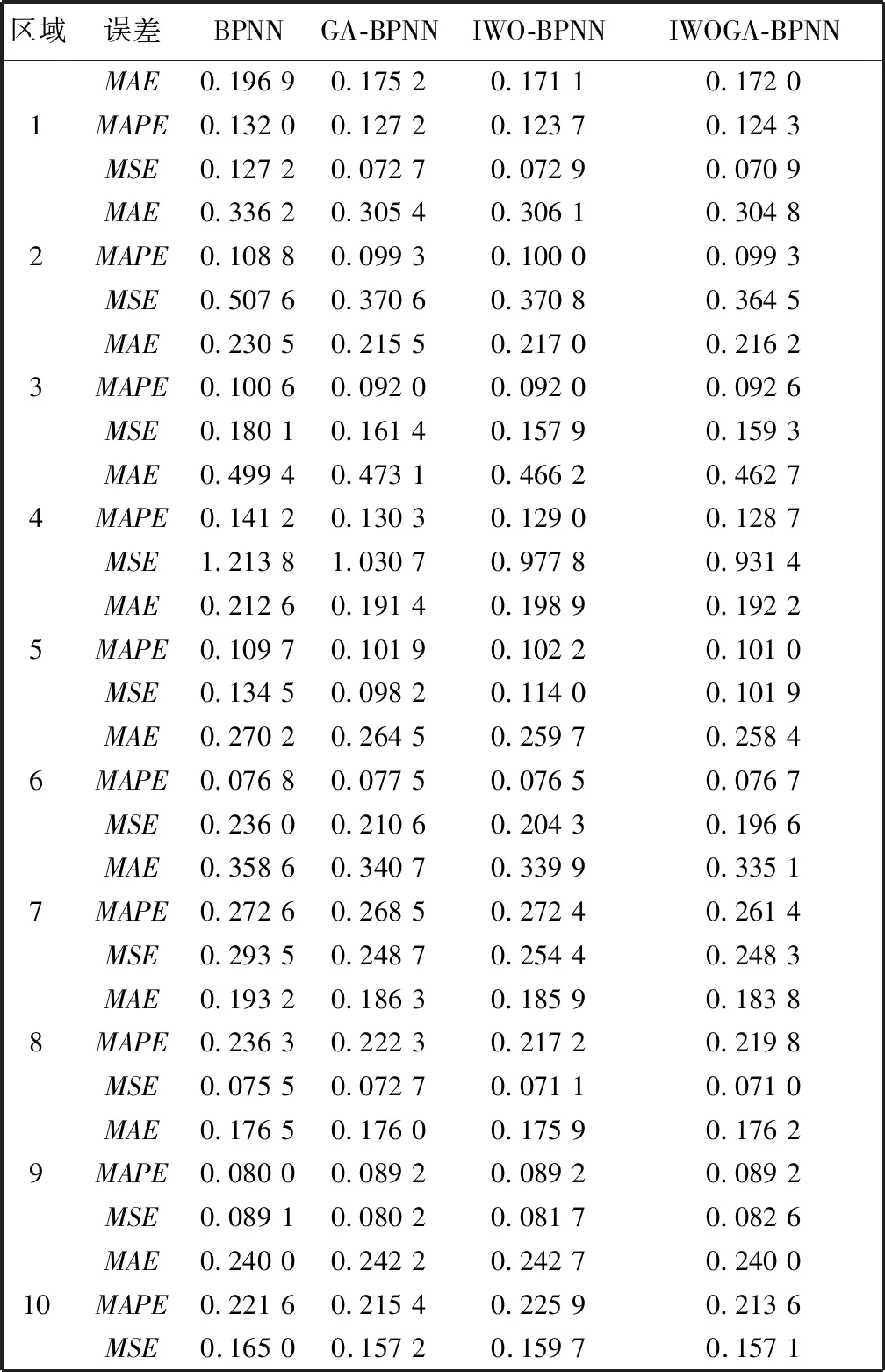
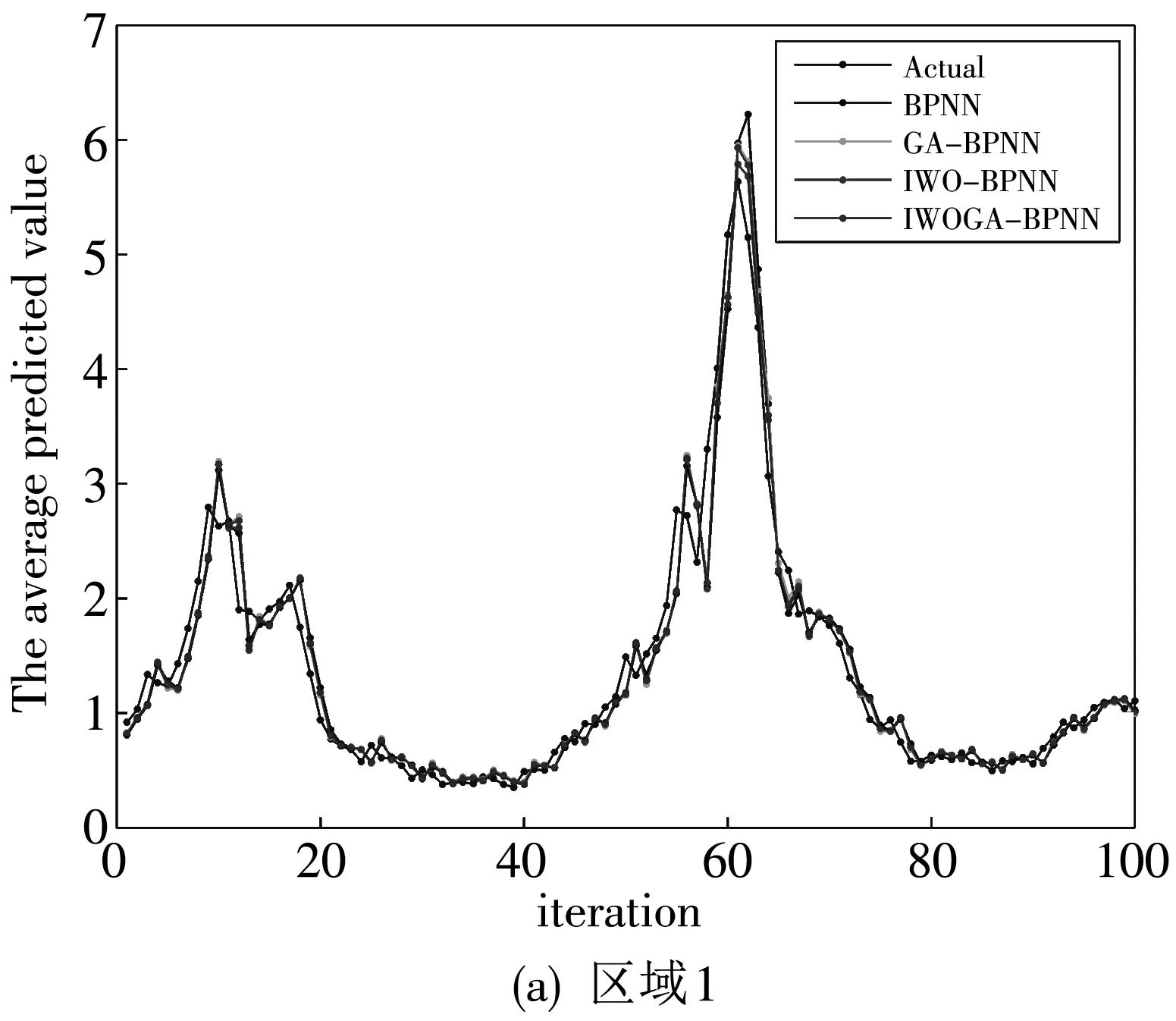
步骤3: 利用交叉概率Pc(0 3) 变异. 变异算子模拟了在自然进化中个体的某些基因的变异现象. 这样根据变异概率Pm获得新个体. 变异算子是保持个体多样性的重要方法. 2006年,A.R. Mehrabian和C. Lucas 提出了一种简单但有效的基于杂草繁殖的数值随机优化算法:入侵性杂草优化(IWO)算法[10]. 1.2.1 任意初始化 P表示种群,其大小为Psize. 初始化参数:最大的迭代数itermax, 最大种子数Smax,最小种子数Smin, 非线性调制指数m, 标准差σ的初始值σinitial, 最终值σfinal. 初始解种群扩散到d维空间的任意位置. 1.2.2 繁殖 根据其自身和群体的最低和最高适应度,确保每棵杂草能线性增长产生种子. 图 1 是种子的生产过程,图中:max fitness in the colony 表示群体中的最大适应度值,plant’s fitness表示植物的适应度值,min fitness in the colony表示群体中的最小适应度值,min no. of seeds表示种子的最小数目,max no. of seeds表示种子的最大数目,no. of seeds表示种子的数目,floor表示取整. 每棵杂草产生的种子的数目通过图 1 获得, 如下: no.ofseeds=floor(minno.ofseeds+ (fitness-minfitness)). (1) 1.2.3 空间扩散 在IWO中, 在d维搜索空间以均值为0,可变方差为σ2的正态分布随机数任意分布所产生的杂草. 这就意味这杂草能够任意分布使得他们住在靠近母体的地方. 然而,在每步中随机函数的标准差σ是从σinitial到σfinal减少的,定义为 (2) 式中:σiter是当前迭代iter的标准差,这使得在每一个时间步,在远处落下一粒种子的概率非线性下降,从而根据适应度值得到新种群优于前种群. 这样r-选择机制转化为K-选择机制. 图 1 种子生产过程Fig.1 The productive process of the seed 1.2.4 竞争排斥 在自然中,种子的存在使得整个世界生机焕然. 因此,控制种群的大小保证了植物间的相互竞争. 多次迭代后,通过快速繁殖种子的数目达到最大值pmax. 然而,具有较好适应度值的植物多于具有不好适应度值的植物. 因此,根据竞争存活规则,每颗种子执行繁殖和空间扩散. 然后所产生后代和种群中的种子的适应度值按照从小到大排序,当种子数超过Psize, 选择Psize个最小适应度值的种子构成新的种群,其余种子舍弃不用. 在GA的选择算子中,每个个体根据IWO中每个杂草的种子数产生他的复制品. 然后按照适应度值从小到大的顺序个体,选择前N个个体构成新的种群. 这样IWO和GA组合建立了新颖的混合算法,记为IWOGA. 在IWOGA中,选择的交叉算子是单点交叉. 将种群中的每个个体映射到只含一个隐含层的BP神经网络的权值和偏差,建立了预测模型IWOGA-BPNN. IWOGA-BPNN的流程图如图 2 所示. 图 2 IWOGA-BPNN的流程图Fig.2 The flow chart of IWOGA-BPNN IWOGA-BPNN预测模型的具体步骤如下: 步骤1:初始化参数: 种群大小Psize, 最大迭代次数itermax, 最大种子数Smax, 最小种子数Smin, 交叉概率Pc, 变异概率Pm, 非线性调制指数m, 标准差σ的初始值σinitial, 最终值σfinal, 每个个体的基因数n, 基因的上界ub和lb. 训练样本为P=(Pij)r×Q, 对应的目标输出为T=(tk)1×Q. 令t=0. 步骤2:初始化种群: pop(i,j)=lb+rand()*(ub-lb), (i=1,2,…,Psize;j=1,2,…,n). (3) 步骤3:计算种群中每个个体的适应度值. 将第i个个体pop(i,:)映射为BP神经网络的隐含层的权值、偏差和输出层的权值、偏差,输入训练样本P和目标输出T训练BP神经网路,得到训练样本对应的输出O, 将O与T之间的均方差MSE作为第i个个体pop(i,:)的适应度值,即第i个个体pop(i,:)的适应度值为 (4) 步骤4:对这个种群进行GA的选择算子操作. 对每个个体根据IWO中每个杂草的种子数(1)根据式(2)得到它的子代,然后根据步骤3得到个体和其子代的适应度值. 所有个体和其子代按照适应值从小到大排序,前Psize个适应度值对应的个体构成新的种群,确定最优个体. 步骤5:根据交叉概率Pc对种群进行GA的交叉算子操作,得到新的种群. 根据步骤3得到个体的适应度值,确定最优个体. 步骤6:根据变异概率Pc对种群进行GA的变异算子操作,得到新的种群. 根据步骤3得到个体的适应度值,确定最优个体. 步骤7:判断是否满足终止条件t>itermax. 若否,令t=t+1,转到步骤4. 若是,映射最优个体到BP神经网络的隐含层的权值、偏差和输出层的权值、偏差,输入训练样本P和目标输出T来训练BP神经网络,得到了IWOGA-BPNN预测模型,将测试样本输入到已训练好的BP神经网络,即IWOGA-BPNN预测模型,得到测试样本的预测输出. 本文所采用的数据来源于网站 https://gis.cdc.gov/grasp/fuview/fuportaldashboard.html[19],下载从2009年第35周到2018年第45周的CDC数据包括健康与公共事业(HHS)所定义的美国10个区域的加权的%ILI,未加权的%ILI,年龄在0~4,5~24,25~64岁之间和65岁以上的病人数,ILI病人总数和总的病人数. 本文选取其中的未加权的%ILI的CDC数据进行预测. 为了评价预测算法,本文所采用的评判标准是平均绝对误差(MAE),均方差误差(MSE),平均绝对百分比误差 (MAPE),定义为 (5) (6) (7) 本文建立了模型 IWOGA-BPNN来预测美国未加权的%ILI. IWOGA-BPNN的输入数据是由第(t-1)th,(t-2)th, (t-3)th周的未加权的%ILI构成,输出是第tth周的未加权的%ILI. 这样获得了477个3维输入数据,其中,377个数据作为训练数据,100个数据作为测试数据. 本文用来比较的预测未加权的%ILI的模型有:BPNN,GA-BPNN, IWO-BPNN 和IWOGA-BPNN. BPNN, GA-BPNN, IWO-BPNN 和IWOGA-BPNN的BPNN部分采用的是只有一个隐含层的BP神经网络,且隐含层的结点个数是6, 训练的最大迭代数是 3 000,学习率是0.1,动量因子是0.8,训练目标是 0.000 000 1. 另外,GA,IWO 和IWOGA中的种群大小是30,迭代次数是100次. BPNN, GA-BPNN, IWO-BPNN 和IWOGA-BPNN分别独立运用10次,获得运行结果,如表 1,图 3 和图 4 所示. 表 1 10个区域的评价标准MAE,MAPE,MSE 表 1 是这10次独立实验运行的平均MAE,MAPE和MSE. 由表 1 可见,IWOGA-BPNN运行的MAE,MAPE和MSE在区域2,区域4,区域7和区域10达到最小值. IWO-BPNN的平均MAE和MAPE在区域2,区域4,区域5,区域7 和区域10达到最小值. IWO-BPNN的平均MAE和MSE在区域2,区域4,区域6,区域7, 区域8 和区域10达到最小值. IWO-BPNN的平均MSE在区域1,区域2,区域4,区域6,区域7, 区域8 和区域10达到最小值. IWO-BPNN的平均MAPE在区域2,区域4,区域5,区域7,区域9 和区域10达到最小值. 图 3 是BPNN, GA-BPNN, IWO-BPNN 和IWOGA-BPNN的预测值与实际值的曲线对比图,而图 4 是BPNN, GA-BPNN, IWO-BPNN 和IWOGA-BPNN的预测值与实际值的差值对比图. 通过这四个模型的比较可以得出:本文所提出的IWOGA-BPNN优于BPNN, GA-BPNN, IWO-BPNN, 适合预测未加权的%ILI. 本文是在GA的基础上,将IWO的繁殖引进到GA的选择算子中,提出了基于GA和IWO的混合算法 IWOGA, 并且将IWOGA优化BP神经网络的权值和偏差实现美国未加权的%ILI预测. 实验结果表明所提出的IWOGA-BPNN适合美国未加权的%ILI预测.1.2 入侵性杂草优化算法
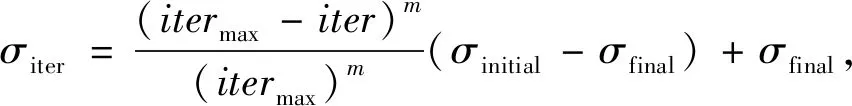
2 预测模型
2.1 基于GA和IWO的混合算法
2.2 预测模型



3 实验
3.1 数据源




3.2 实验结果




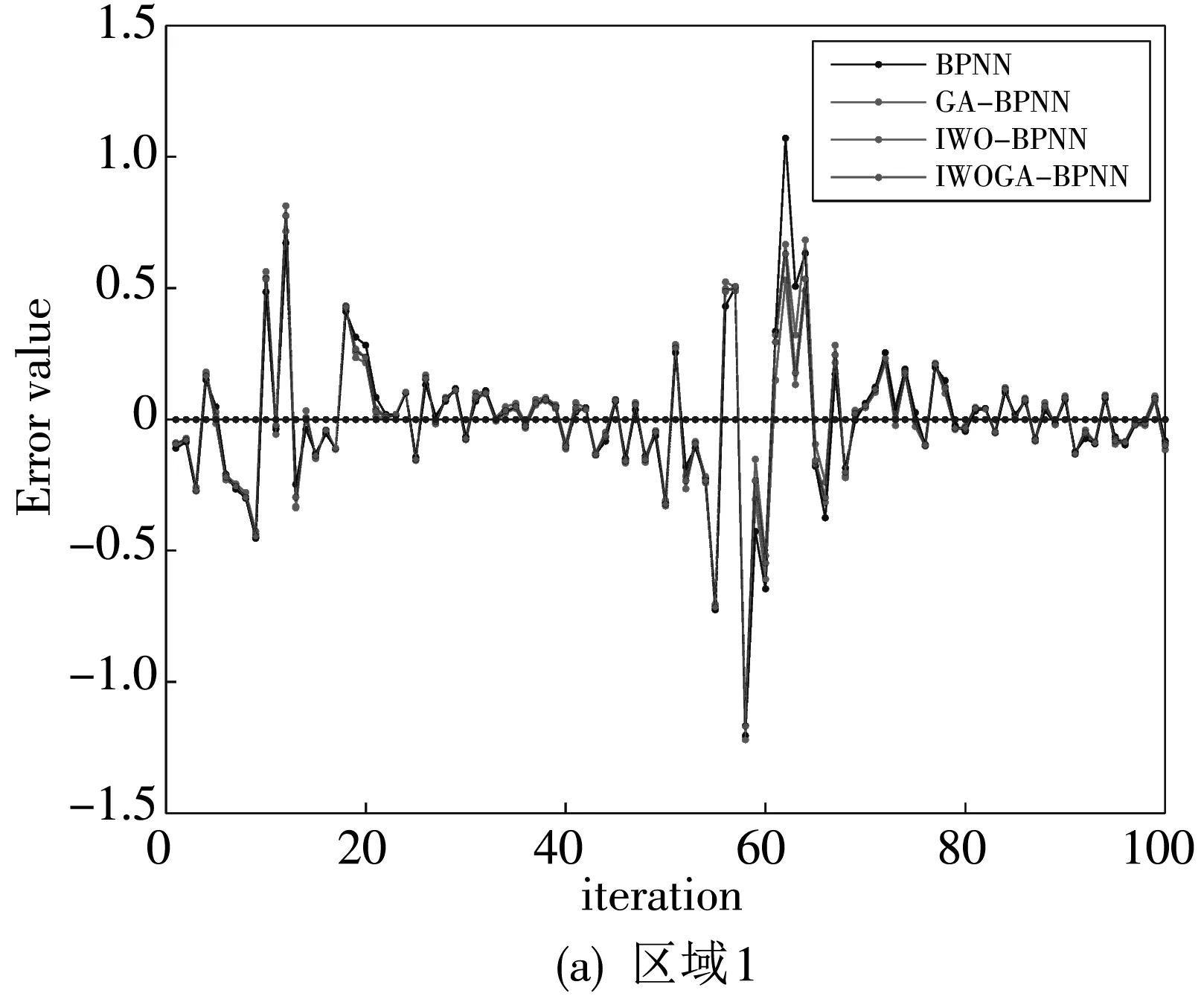
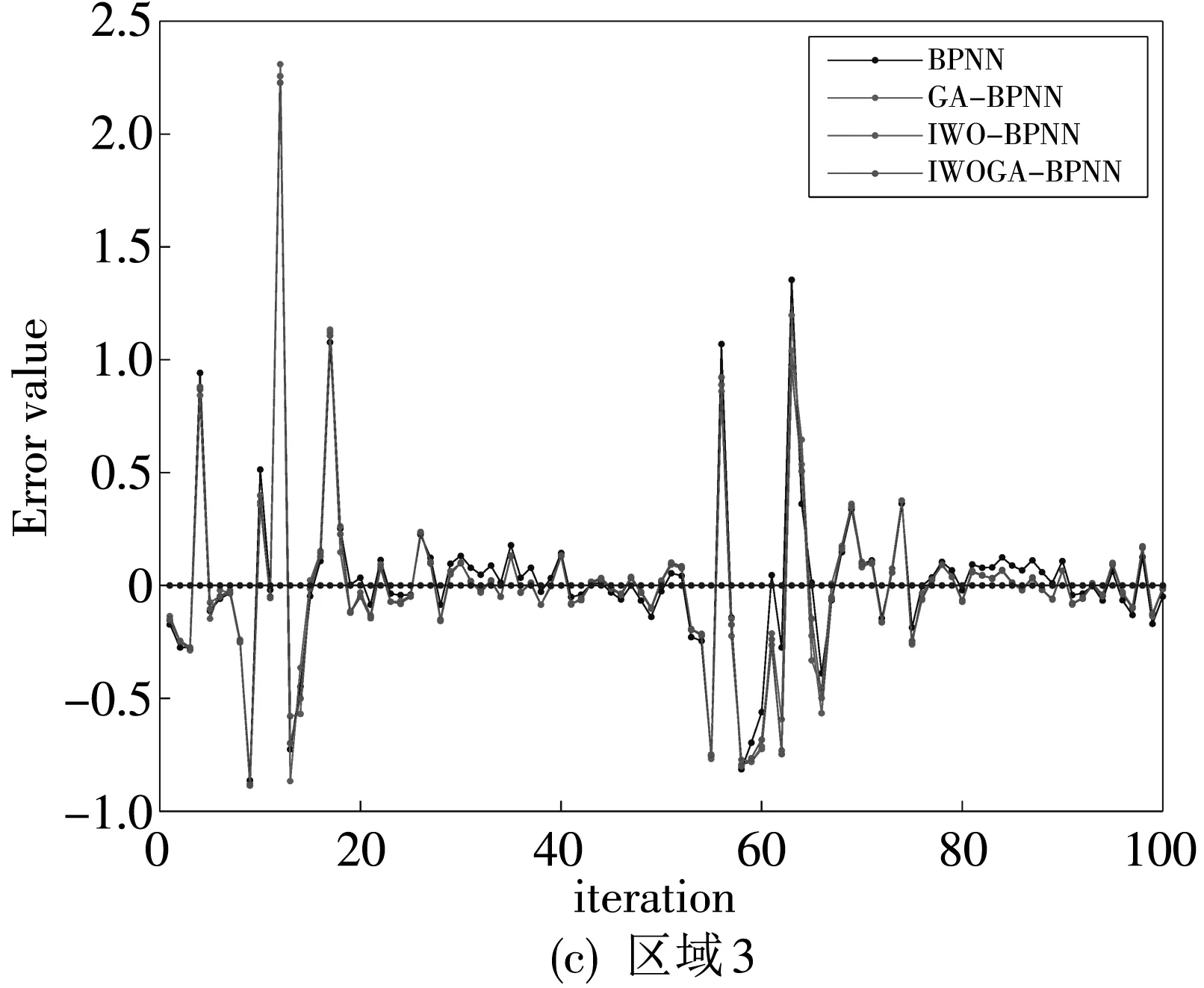



4 结 论
