二维三轴编织复合材料预压单胞模型建立及其弹性规律数值预测

2019-10-29张芳芳段永川

纺织学报 2019年10期

张芳芳，段永川

(1. 燕山大学机械工程学院，河北秦皇岛 066004；2. 燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004)

二维三轴编织复合材料由3个方向的纤维束在平面内相互编织而成，这样在不同角度下可兼顾材料的横向力学行为，有效克服传统层合板力学性能差的缺点。由于编织复合材料中纤维束相互交织，因此，编织纤维束的截面形状在不同位置会发生畸变，构造实际的纤维束几何模型已十分困难，如果再对纤维束几何模型离散网格构造有限元模型更加困难。

目前多数学者都是基于一定的模型简化来构造编织复合材料的几何和有限元网格模型。Tsai等[1]采用弹簧单元建立了简化的单胞网格模型，并对弹性力学参数进行了预测。Miravete等[2]通过沿编织方向增加4条边界线，建立了简化的“米”字形单胞模型，虽降低了构造模型的难度，但也降低了复合材料弹性、损伤等力学性能的预测精度。Benzley等[3]通过模拟对比得出，六面体单元具有更多的自由度和抗畸变能力，在力学性能预测时能得到更高的精度[4-5]。Kim等[6]采用一种体素单元法建立了复合材料模型，该方法在表征复合材料两相材料的交界面时精度降低，但这种方法随着分辨率的提高，可消除这个问题。Gao等[7]假设纱线横截面为矩形，建立出二维三轴编织预制件的动态几何模型。严雪等[8]基于传统有限元建模方法建立了考虑纤维束弯曲扭转和空间交错特征的有限元模型，并预测了其弹性性能规律。Kier等[9]假设纤维束横截面为椭圆形，编织纤维束路径为正弦曲线，利用CAD软件生动再现了二维三轴编织复合材料的几何模型。张芳芳等[10-11]基于直线的纤维束路径建立了三维编织复合材料模型，并对其进行了损伤分析，然而当纤维束路径波动较大时预测误差会逐渐增大。

目前学者大都利用简化模型对材料的微观形态进行表征，但复合材料纤维束在固化时会受到一定的挤压变形，空间形态改变会对材料的弹性及损伤等性能造成影响。基于此，本文提出基于力学原理考虑空间挤压的模型快速建立方法。利用变形后纤维束空间分布及形态再形成体素单胞模型，基于该模型预测了二维三轴编织复合材料的弹性规律。

1 细观几何模型

1.1 编织结构

二维三轴编织复合材料的编织结构如图1所示。复合材料由3个方向的纤维束组成，其中与y轴平行的为直纤维束，另外2个方向为编织纤维束，他们沿着轴向纤维束相互交织，在z轴方向上看，轴向纤维束位于2个编织纤维束中间，在厚度方向上轴向纤维束位于材料中间。图中白色框为一个周期单元，称为一个单胞，其宽度为W，高度为L，编织角指轴向纤维束与编织向纤维束所夹的锐角(见图1 中α)，单胞内编织向纤维束长Lb。在图中所示坐标系下，y轴与复合材料轴向纤维束的轴线平行，x轴与复合材料轴向纤维束的轴向垂直。z轴与复合材料的厚度方向平行。

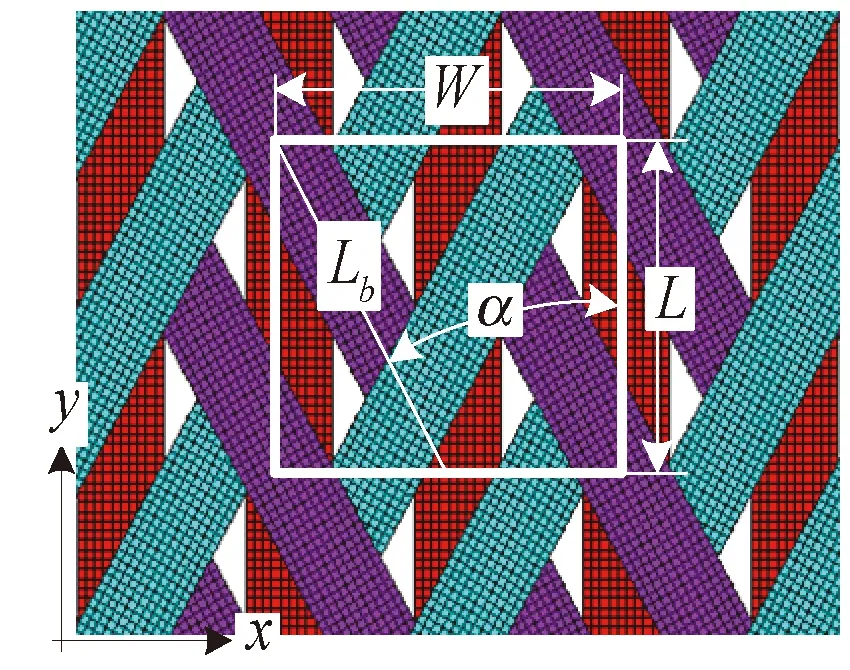
图1 二维三轴编织复合材料的结构示意图

将纤维束中心线定义为空间函数，选用三次样条曲线描述纤维束路径，其中第i段样条曲线pi(t)的参数方程一般形式为

pi(t)=Ai+Bit+Cit2+Dit3

(1)

式中：t为该样条曲线的参数， 0≤t≤1,i=0,1,…,n-2，Ai、Bi、Ci、Di分别为第i段样条曲线的幂次项系数向量。该方程是在单胞内定义，在单胞两端面上要满足几何连续性，在样条曲线的起始点处应满足的连续条件为

p″0(0)=p″n-2(1)

(2)

为验证样条曲线建立的正确性，在空间取了5个坐标点，每个坐标点的坐标分别为(0,0,0)，(0.5,0.7,0.4)，(1,0.6,0.0)，(1.5,0.7,-0.4)和(2,1.2,0)。在边界约束条件下生成的周期样条曲线如图2所示。可以看出，样条线光滑连续，可以满足实际要求。

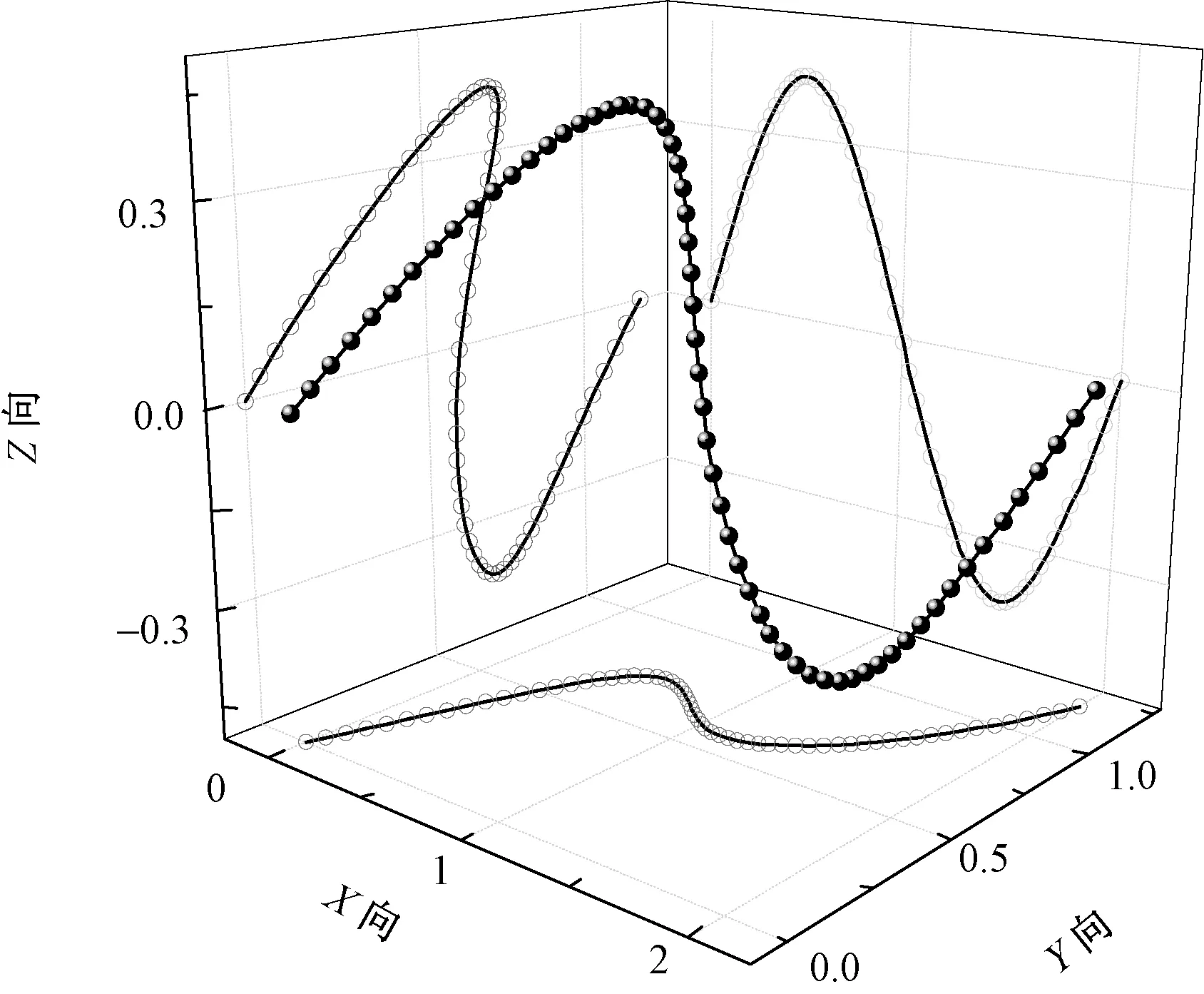
图2 周期性空间样条曲线

参考文献[12]中的纤维束横截面拓扑形状，将纤维束的横截面假设为透镜形，如图3所示。透镜形纤维束横截面由半径分别为r1和r2的2个圆相交而得，2个圆各自偏离图中坐标系横轴的距离是o1和o2。参数r1、r2、o1和o2可根据透镜的宽度w、高度h和偏移距离d计算得到。

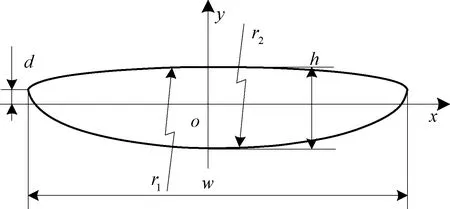
图3 透镜形纤维束截面

透镜形横截面的参数方程为：

(3)

(4)

(5)

(6)

(7)

1.2 编织结构参数

根据图1所示几何关系，单胞内编织向纤维长Lb为

(8)

式中：L为单胞高度，mm；α为编织角，(°)。

定义轴向纤维束横截面面积为Aa及圆弧段所对圆心角为αa，其计算公式分别为：

(9)

(10)

式中：ra为圆弧段的半径，mm；w、h分别为透镜形截面的宽度和高度，mm。同理，可计算出编织向纤维束横截面面积Ab和圆心角αb。从图1可以看出，在一个矩形单胞模型中含有2根轴向纤维束和4根编织向纤维束，则编织向纤维束和轴向纤维束的体积分别为：

Va=2AaLa

(11)

Vb=4AbLb

(12)

(13)

式中：Va、Vb分别为单胞中轴线纤维束和编织向纤维束的体积，mm3；Aa、Ab分别为轴线纤维束和编织向纤维束的横截面面积，mm2；La、Lb分别为单胞中轴线纤维束和编织向纤维束的长度，mm；Vf为单胞中的纤维体积含量，%；L、W、H分别为单胞模型的长度、宽度和高度，mm；φ为纱线填充因子，本文认为编织向纤维束与轴向纤维束的纱线填充因子相同。

2 体素法建立有限元模型

2.1 单元材料主方向计算

纤维束在空间的走向可以用其中心线在空间的走向进行描述，由于纤维束路径的波动导致纤维束各个部位有着不同的材料主方向。应用有限元方法对实体模型进行离散后，为准确地描述各单元的材料主方向，需要计算单元形心处的材料主方向，如图4所示。令第i段曲线中某单元的形心点为P，过该点做垂直于纤维束中心线的平面，计算出该平面与纤维束中心线的交点，交点处的参数坐标为tp，该交点沿纤维束走向的切线向量P′i(tp)计算方程为：

P′i(tp)·(P-Pi(tp))=0

(14)

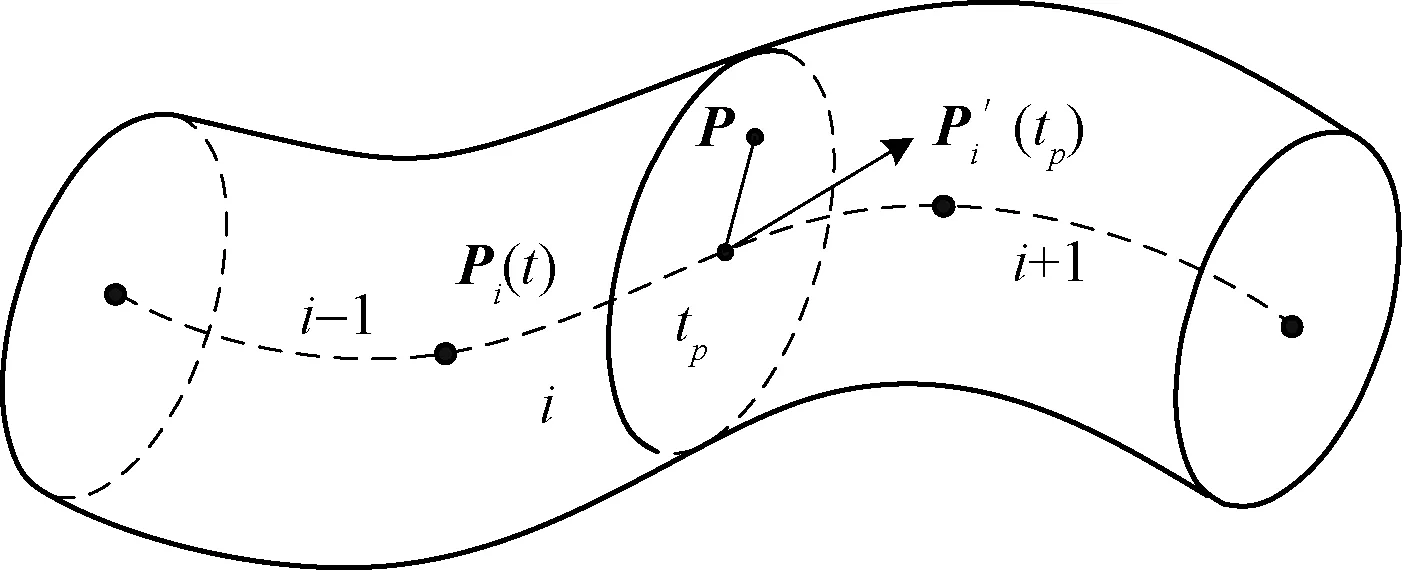
图4 纤维方向求解

依据右手法则，确定单元材料坐标系与总体坐标系的变换方向和角度。本文采用ANSYS软件对有限元模型进行建立和计算，在该软件内采用LOCAL命令为每个单元建立局部坐标系，该坐标系采用2个相对转动角度θxy和θxz定义，如图5所示。假设一个单元的纤维方向为L(x,y,z)，L(x,y,z)与图中坐标系的z轴构成一个平面，其法线方向为D(x,y,z)。

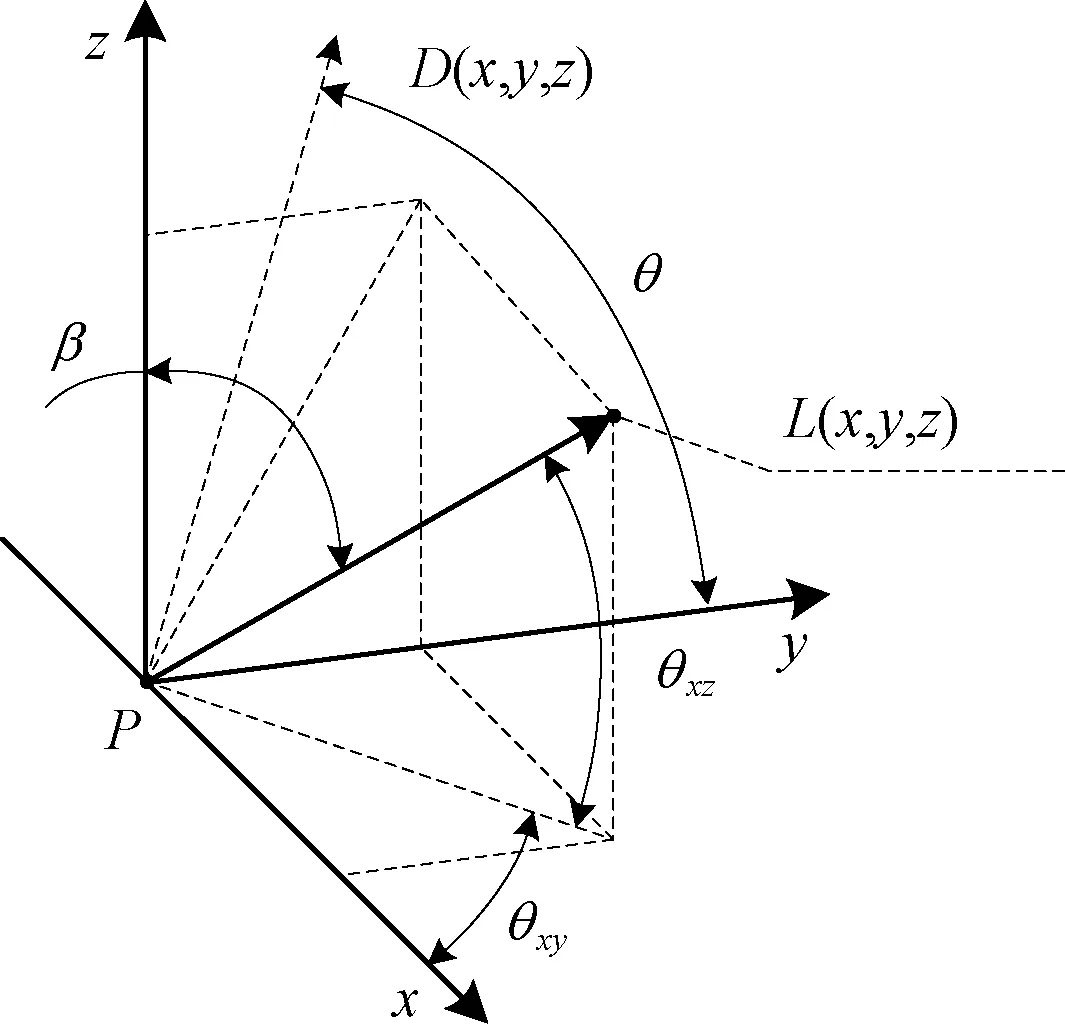
图5 材料主方向转角定义

图5中x、y和z轴与全局笛卡尔坐标系的三轴平行，其中θ为y轴与向量D所形成的锐角，β为向量L与z轴所成锐角，2个相对转角θxy和θxz的计算公式为：

(15)

(16)

2.2 挤压力学模型的建立

为考虑纤维束间的挤压扭曲影响，首先建立二维三轴编织预制件模型如图6(a)所示。因预制件未与基质黏接固化，无法构造固化后预制件的周期单胞，对预制件进行预压时，采用材料的真实边界进行约束，一个中心单胞利用其领域内8个单胞进行自然边界的约束。在预制件有限元模型中纤维上下表面分别加入接触单元，在上下2层分别利用平面进行一定的预压缩，将预制件模型厚度压缩至目标单胞模型厚度，从而得到纤维束呈挤压接触状态下的几何形态。开发周期单胞提取程序，该程序基于FORTRAN语言编写，具有与ANSYS软件兼容的进出接口，首先将变形后的单元节点信息导出，给出切取单胞的边界盒坐标，在边界面上程序可自动细分单元，完成周期单胞单元提取。为便于后期处理，提取前对不同方位的纤维束进行集合划分，单元切割程序可保持单元的集合和单元坐标系的继承能力，多个单元可能由一个父单元切割再分而来，这几个单元就要保持与父单元同样的集合和单元坐标系方位。切割出的增强相单胞网格模型，如图6(b)所示。切割出的增强相单胞模型单元坐标系方位显示如图6(c)所示。

图6 二维三轴编织预制件网格提取

2.3 体素网格模型的建立

应用上述切割算法已经获取了变形后纤维束单胞模型，本文利用体素模型法建立变形后的单胞模型，在该模型区域内填充正方体素单元。根据已提取的预制件单胞单元来对所填充的正方体素单元进行集合创建与单元坐标系的继承。利用预制件单胞单元在每根纤维束表面生成表面单元，然后判断体素单元与表面单元的相对位置，当体素单元的形心坐标在表面单元的包络区域内时，将该体素单元纳入该集合内，其他纤维束计算方法相似，最后生成的体素模型如图7所示。

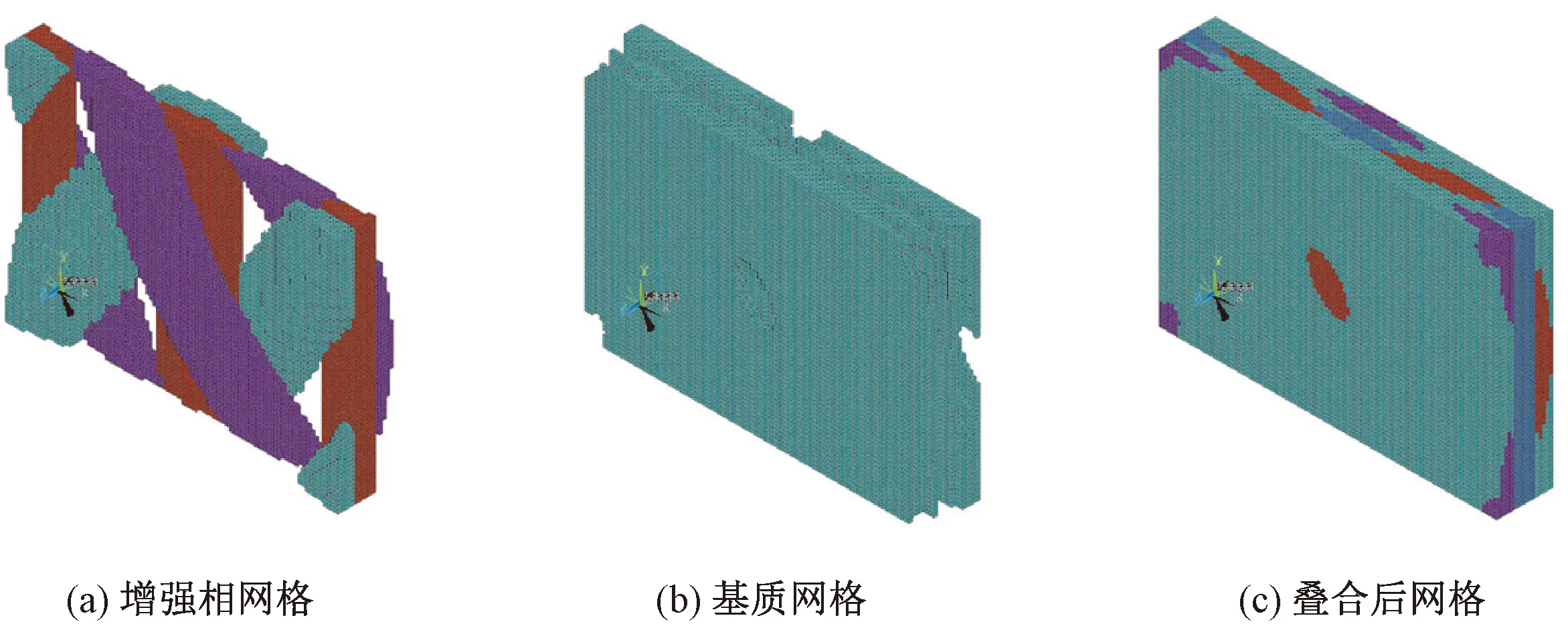
图7 采用体素法建立的复合材料单胞网格模型

该模型采用全正方六面体网格建立，边界非常容易满足边界节点一一对应的关系。

3 周期性边界条件

复合材料内部细观结构周期重复，在外载荷作用下其应力应变场同样满足周期重复性，为降低计算量，选取一个代表单元进行力学行为预测，在单胞2个对应的边界面建立周期对应的耦合约束方程[13]，约束表达式如下:

(i,j,k=x,y,z)

(17)

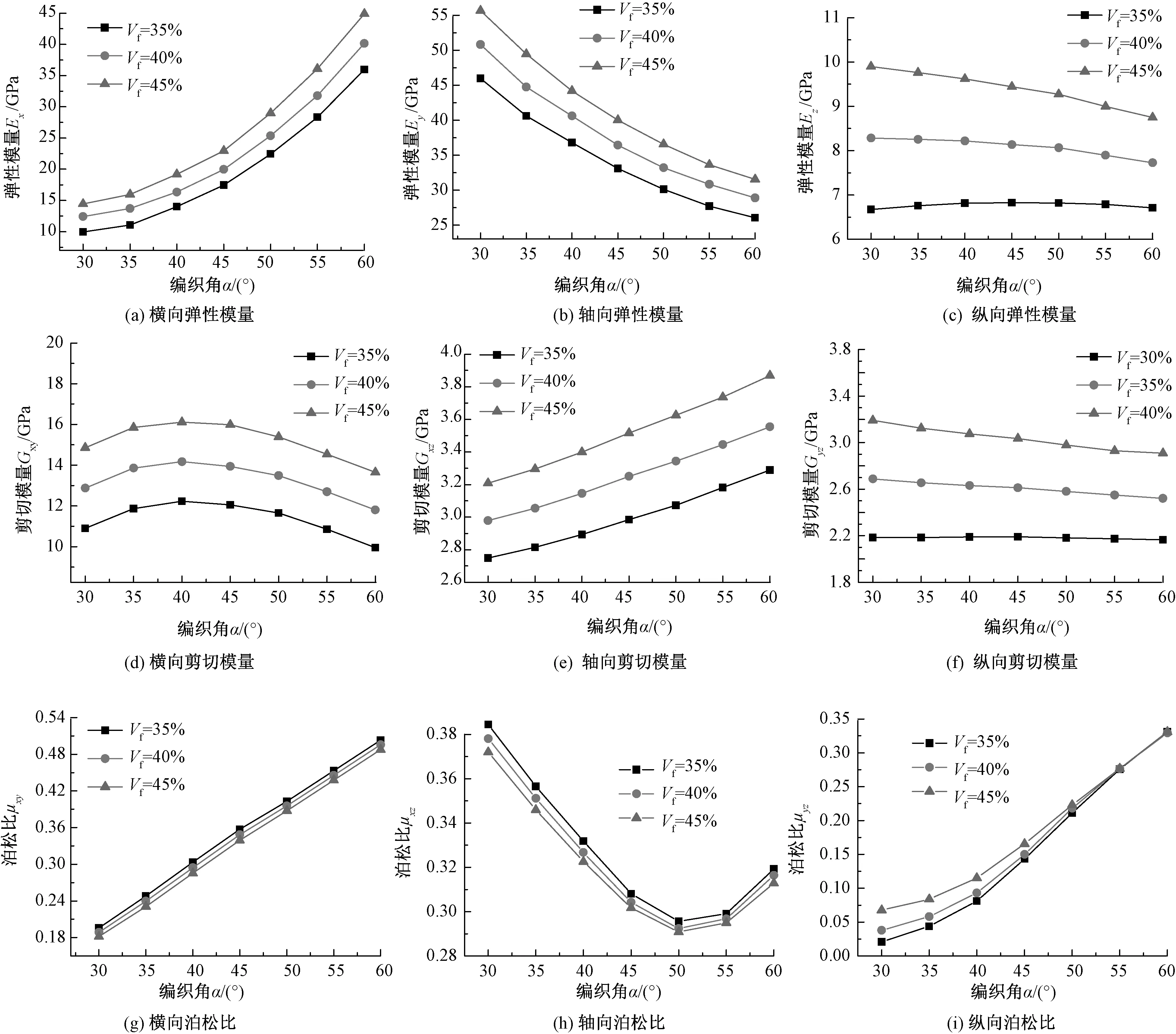
图8 编织角和纤维体积含量对二维三轴编织复合材料横向和轴向模量的影响

4 结果分析

以文献[12]中所提供的实验数据进行对比验证，模型中所采用的材料组分力学性能参数如表1所示。为验证体素模型的收敛性，不同编织角和纤维体积含量下分别建立了3组不同网格密度的体素模型，进行轴向模量的预测，并与实验结果进行对比，结果如表2所示。随着体素模型网格密度的增加，预测出的轴向弹性模量变化不大，认为得到收敛解。二维三轴编织复合材料的力学行为主要受编织角和纤维体积含量影响，在不同编织角和不同纤维体积含量下材料宏观力学行为的变化规律如图8所示。

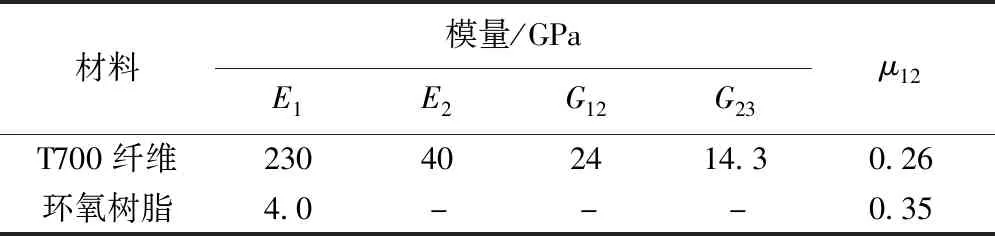
表1 组分材料性能参数

从图8(a)可见，随着纤维体积含量的升高，二维三轴编织复合材料横向，即坐标系的x轴方向的弹性模量Ex有所升高，在材料内部主要靠纤维束承载，当预压缩提高纤维含量时材料的弹性性能有所升高。

表2 数值预测结果与实验对比

从图8(b)可以看出，随着纤维体积含量的升高，材料轴向即坐标系的y轴方向的弹性模量Ey有所升高，其升高原因与横向模量相似。随着编织角的增大，材料的横向弹性模量Ex不断升高，当编织角升高时，轴向纤维束以外的两轴方向不断变化，编织角越大，纤维束轴向的性能向单胞横向贡献越多。而材料的轴向弹性模量Ey与横向弹性模量Ex变化规律正好相反。

从图8(c)可发现，当提高纤维体积含量时，材料的纵向弹性性能Ez有所升高，但对材料模量的提高程度较横向和轴向小，随着编织角的增加，3个轴的纤维束交织重叠区域减小，这样造成了在厚度方向上弹性模量逐渐降低，但是降低的幅度很小。

从图8(d)可以看出，当预压缩提高纤维含量时,材料的剪切模量Gxy逐渐增大，随着编织角的增加，剪切模量Gxy逐渐增大而后逐渐减小，当编织角在40°左右时，剪切模量Gxy达到最大值。从图8(e)可以看出，剪切模量Gxz随着纤维体积含量和编织角的增加均呈现出逐渐增大的趋势。从图8(f)可以看出，剪切模量Gyz对纤维体积含量和编织角变化的敏感程度均较低。

从图8(g)可以看出，随着编织角的增加，泊松比μxy呈线性增加，然而改变纤维体积含量对泊松比μxy影响甚微。从图8(h)发现：当提高纤维体积含量时,泊松比μxz逐渐减小，编织角较小时，编织角变化对泊松比影响显著；随着编织角的增加，泊松比近似呈线性降低，当编织角大于40°后，编织角变化对泊松比的影响程度逐渐降低。从图8(i)可以看出：泊松比μyz随着编织角的增加呈现先减小后增大的变化趋势，并且在编织角较小时，纤维体积含量的变化对泊松比影响很大；当编织角小于40°，预压缩提高纤维含量时,泊松比μyz有较大幅度的增加；当编织角大于40°时，纤维体积含量变化对泊松比的影响程度逐渐降低；当编织角达到50°时，纤维体积含量变化对泊松比的影响程度几乎为零。