基于多级细分的彩色模型表面体素化算法
2022-12-05张祥云周正友
王 莉,张祥云,周正友
(1.西安交通大学 机械制造系统工程国家重点实验室,陕西 西安 710049;2.西安增材制造国家研究院有限公司,陕西 西安 710399)
0 引言
近年来,基于体素的三维模型的概念被首次提出,并逐渐引起各领域研究工作者的重视。相较于传统采用几何多边形表达物体几何信息的三维模型,体素模型是一种采用大量规则体素的有序组合来表示三维物体的模型。体素模型的基本单元体素与二维空间中的像素类似,是数字数据于三维空间分割上的最小单位,可同时包含空间位置、颜色、法向量、材质和透明度等一系列属性[1]。体素模型是一种全信息建模表达方式,其不仅能表达模型的外表形状、颜色等信息,还能描述模型内部的材质属性,因此被广泛应用于三维成像、医学影像、检测碰撞模型,以及体素级多材料3D打印[2-3]和功能梯度材料打印[4,5]等领域。
在增材制造领域,聚合物喷射成型技术(PolyJet)、立体喷墨打印技术(Three-Dimension Printing, 3DP)等工艺均具有体素级成型能力。PolyJet工艺通过喷射装置将打印材料以微小液滴的形式排布在打印平面的指定位置处,并使用紫外光照射材料图案使其固化,从而实现体素化3D打印成型。3DP工艺与PolyJet工艺类似,不同的是3DP工艺喷射的是液态粘结剂,将零件截面“印刷”在事先铺平并压实的材料粉末上,喷射的液态粘结剂的各项参数通氧可以实现体素级控制。上述体素级增材制造工艺与三维体素模型相互配合可轻易成型任意复杂材质/色彩的打印件,如多材料模型、复杂功能梯度材料、彩色模型打印成型等。
多材料、多色彩模型打印成型的前提是获取相应的体素模型。在数字模型方面,模型的多材质属性和多色彩属性均可通过色彩进行表示和区分,因此本文将彩色模型作为体素化处理的对象。目前,基于几何多边形的三维模型体素化是获取体素模型的一种重要手段。三维模型体素化算法一般包括表面体素化和内部体素化两部分,本文研究内容主要集中在前者。一种简单的体素化思想是将模型空间均匀分割为空间体素阵列,通过判断模型边界与体素的位置关系标记模型表面体素,从而实现三维模型的表面体素化。一般来说,为得到精确体素模型,通常需要设置较小的体素尺寸。然而在上述操作过程中,随着预设体素尺寸的减小,体素数量和体素化时间将呈指数级增长;同时较大的几何多边形和较小的体素容易导致体素的误标记,从而出现体素缺失、体素模型表面出现孔洞或破裂等问题。针对上述问题,研究者展开了广泛的研究,并提出了不同的解决方法。
SZUCKI等[6]在均匀体素模型的基础上,进一步将特征区域的体素细分为N×N×N个子体素,仅保留子体素中与模型相交的部分,从而得到多分辨率体素模型。BERGS等[7]以边界表示模型所在空间作为根节点,通过递归地将根节点空间分割为8个相等的立方体,检查并保留与模型相交的子节点,保留下来的子节点体素又将作为下一级分割的父节点,重复上述步骤直至达到预设体素阈值或者递归深度,最终得到原始模型的体素化表示。该算法中,边界表示模型的多边形尺寸决定了八叉树分割的体素阈值不能太小,否则可能导致得到的体素模型表面出现孔洞或破裂等缺陷。穆斌等[8]针对当前体素化算法效率低的问题,提出一种“家谱”式的八叉树节点位置描述方法,大大提高了八叉树节点检索效率。此外,通过投影面积判断体素与模型的位置关系,完成模型的实体体素化,但该算法计算量较大。王鸿亮等[9]提出一种基于“树型结构和线性结构”双层次八叉树模型及其编码规则,利用树型结构实现体素位置的快速定位,而线性结构能更准确地表达实体边界和模型内部空间,两者的结合较好地平衡时间和空间特性,实现STL模型高效准确体素化。刘晨燕等[10]针对体素模型表面分辨率增加时,体素化时间和体素数量急剧增长的问题,提出基于边界状态约束的表面体素细分算法,通过多级加密获得多分辨率体素模型。该算法提供了一种三维模型的多级实体体素化表示,但在表面体素化方面并不具备明显优势。赵芳垒等[11]提出一种基于STL模型的表面体素化算法,通过细分三角面片顶点并建立细分顶点和体素间的关系,基本实现了表面体素化的过程,但该算法过程中产生的体素数量随体素化分辨率的增加而急剧增加,因此难以满足较高分辨率的体素化需求。此外,部分研究者尝试使用图像处理器(Graphics Processing Unit, GPU)以提高体素化效率,如YOUNG等[12]利用GPU强大的并行计算能力,提出一种基于GPU加速的边界表示模型的多级体素化算法。在生成边界表示模型的体素化表示上,该算法比CPU体素化算法快40倍。
综上所述,多种三维模型表面体素化算法被提出来提升体素模型分辨率和体素化效率、减少体素数量,但均存在缺陷,如:通过“均一体素模型+局部线性细分”算法得到的模型细节加密处过渡不平滑;随着体素分辨率增加,八叉树数据结构导致体素数量呈指数级增加;基于硬件加速的体素化算法对硬件依赖性高,通用性不强等。此外,上述算法未考虑模型包围盒尺寸对体素化精度的影响,且在得到的体素化表示在模型曲率较小处容易出现孔洞或破裂等缺陷。此外,体素模型的材质定义也尚未涉及,而这对于体素级增材制造技术是十分重要的。
针对上述问题,本文提出一种基于八叉树分割和线性细分的彩色模型表面体素化方法。该方法首先通过均匀细分三角面片获取模型体素化所需的加密点云数据;然后以三维模型包围盒空间为根节点建立空间八叉树数据结构,通过一分为八的方式逐步细分表面体素,并删除非表面体素,获得较高分辨率表面体素模型。在此基础上,通过M×N×K线性加密叶节点体素,将叶节点体素规范至接近立方体的状态,极大地提升了体素模型的精度。通过色彩插值和一种基于距离影响因子的体素颜色计算方法完成表面体素色彩值的定义。
1 模型数据预处理
1.1 OBJ格式文件
为研究彩色模型表面体素化算法及其在彩色3D打印中的应用,本文选择OBJ格式模型作为研究对象。相比于增材制造领域的标准输入文件格式STL,OBJ模型文件同时包含了模型的几何信息、模型表面颜色信息和模型材质信息,这一特点正好契合于多材料增材制造对于打印材质和颜色分布描述的需求。
OBJ文件本质上是一种文本文件,其通过关键字对三维模型的点、线、面等信息进行标记区分和存储,OBJ文件中主要的数据类型如表1所示。

表1 OBJ三维模型文件格式说明
1.2 算法实现总流程
本文的算法流程如图1所示,具体实施步骤如下:
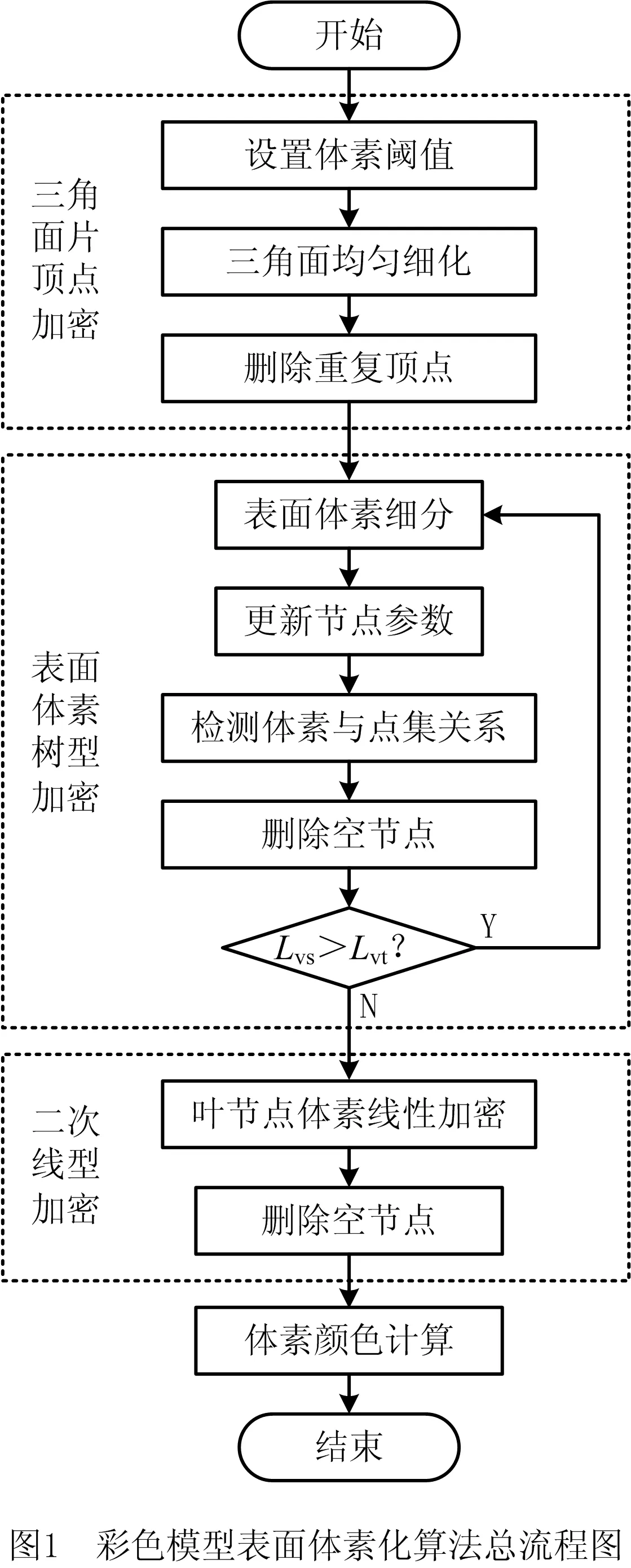
步骤1三角面片顶点加密。算法执行之前需要输入体素阈值Lvt作为三角面片细分依据和体素分割的终止条件。在表面体素分割过程中,为避免部分三角面片过大导致的体素信息缺失、体素模型表面破裂等现象,对模型三角面片网格进行均匀细分加密,以保证生成的表面体素能够完全封闭。
步骤2表面体素树型分割。首先以三维模型包围盒空间为八叉树根节点,通过一分为八的方式逐步完成模型体素化过程。在八叉树细分过程中不断检测体素与点集的关系,将包含有点集的体素设为非空节点,否则为空节点,并删除空点。使用八分法均匀分割非空节点体素,并以八叉树结构进行存储。每次完成体素细分后,均需检测子体素与点集的状态,并删除空节点。不断重复上述步骤,直至表面体素最小边小于预设的体素阈值。
步骤3二次线型加密。考虑到模型包围盒形状对体素形状和体素模型精度的影响,提出一种体素线性加密方法,即将八叉树最后一层的体素在空间三方向上同时均匀分割,使得加密后的体素三方向上的尺寸均满足体素阈值的要求。二次线性细分极大地提高了体素模型的精度,同时也避免了过大的体素数量。
步骤4表面体素颜色计算。本文提出一种基于距离影响因子的体素颜色计算方法。选择距离某体素最近的4个顶点颜色为该体素的颜色影响点,按照距离越远影响越小的标准,计算表面体素的颜色,完成体素模型的颜色定义。
1.3 三角面片顶点细分算法
在表面体素过程中,需要判断体素与模型的关系,只有与模型表面有交集的体素才会被保留下来。体素与模型关系的判定方法一般分为基于三角面片的判定方法和基于顶点的判定方法两类。前一种方法需要判断体素与三角形的相交关系,若三角面片集合中存在三角形与体素相交,则将其标记为表面体素,否则为空体素。判断三角形与体素相交关系的方法往往计算量较大,如分离轴算法[13]中,对于任意一组体素和三角面片,需要判断二者在13个分离轴方向上的投影是否重叠,计算量十分巨大。后一种通过判断体素与顶点的位置关系确定体素与模型的关系,相较于前一种方法计算量更少,算法效率更高。因此,本文选择后一种方法作为表面体素化方法。
用于描述彩色模型外形的三角面片尺寸差异往往会很大,比如在曲率较小的区域三角面片尺寸较小,而在曲率较大的区域三角面片尺寸变得很大。若对原始模型直接进行八叉树分割,则可能出现如图2所示的情况,即由于三角面片尺寸过大,导致对应体素内部不包含任何一个顶点,因此体素被判定为空节点,继而被删除。该情况下,体素模型精度受到严重影响,甚至可能出现模型表面破裂等现象。

为提高体素模型精度、保证体素模型表面能够完全封闭,有必要对三角面片集进行加密细分,使其能够满足正常体素化对三角面片尺寸的需求。针对这一问题,赵芳垒等[11]提出了一种基于体素细分面积阈值的三角面片细分方法。细分面积阈值是指阈值体素的体对角三角形面积,如图3所示,当模型三角面片面积大于面积阈值时,则需要对三角面片进行分割。
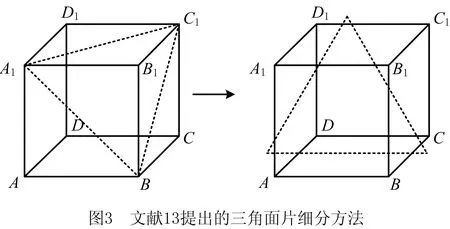
然而该方法细化后的三角面片仍可能导致细分体素的误删,如图3所示,三角形面积大于阈值三角形面积。因此,本文提出了基于最大边长比的三角面均匀细化算法,通过判断三角面片最大边长与阈值体素边长关系决定是否需要加密,满足边长关系的三角面片被均匀细分为多个相似小三角面片,所有小三角面片的并集组成新的顶点数据。单个三角面片加密算法的具体步骤如图4所示。
具体步骤如下:
步骤1对于给定三角面片,首先计算三角形三边边长并选出最大边长Lmax。比较最大边长Lmax和预设的阈值体素边长Lvt,当三角形最大边长大于阈值体素边长时则需要对三角形进行加密。三角形边的分割段数n由式(1)得到:
(1)
式中ceil()为向上取整函数。

步骤2根据步骤1得到的边长分割段数将三角形三边均匀分割成n段,使用平行于三角形三边的线段连接生成的顶点,即可将三角形分割为若干相似小三角形,所有小三角形的顶点集合就是分割后生成的点集。为计算新顶点的坐标,引入两个向量a、b,a和b的方向为三角形相邻两边的逆时针方向,长度为相应两边分割后小线段的长度,如图5所示。对于分割生成的顶点,本文采用向量平移方式,按照三角形的等分层数快速计算其空间位置,并通过线性插值计算新点的色彩信息。因此,三角形分割后产生的全部顶点坐标可表示为:
{(x,y,z)}=(x1,x2,x3)+a×j+b×k;
0≤j≤n,0≤k≤j。
(2)

步骤3在OBJ三维模型中,三角面片的边由两个三角面片共享,三角面片的顶点则由若干个三角面片共享。经过三角形加密细分生成的顶点集合中存在大量重复的点,重复顶点的存在将导致严重的数据冗余,影响算法效率,因此有必要对新生成的点集进行检测,判断并删除重复顶点。为此,本文使用C++标准库容器中的排序算法实现这一目的。经过排序去冗后,得到重采样后无重复的顶点集合。
对模型所有三角面片均质性上述操作后,即得到数据密度足够高的点云数据。将其应用于三维模型表面体素化,将极大地提升表面体素化精度,并有效避免了表面体素误删、体素模型表面破裂等情况。
2 体素模型生成与表面体素细化
2.1 八叉树数据结构
八叉树结构是平面四叉树在空间上的推广,是一种描述三维空间的树状数据结构,常用于三维模型在空间上的表达和存储。在八叉树结构中,所有节点均采取一分为八的方式,如图7所示,因此每个节点都有8个子节点,这8个子节点表达内容的并集与父节点所表达的内容始终是一致的,即八叉树每一层上节点和并集与根节点是等价的。此外八叉树结构中父节点与子节点间的严格逻辑关系,使得八叉树节点的查询和遍历效率大大提高。
因此,本文定义空间八叉树结构节点结构体如下:
typedef struct _OctreeNode
{
ModelColornodeColor;
Vector
double xMin,xMax;
double yMin,yMax;
double zMin,zMax;
struct _OctreeNode * parent;
struct _OctreeNode * child[8];
}OctreeNode;
式中:xMin,xMax,yMin,yMax,zMin,zMax为节点空间的位置信息;parent 为父指针,指向其父节点;child[8]为子指针,指向8个子节点;另外,由于本文研究彩色三维模型的表面体素化,因此增加nodeColor存储节点空间的颜色信息。
2.2 模型空间分割
八叉树各层节点合集始终与根节点等价的特性,使得八叉树能够很好地描述和分割三维空间,因为无论进行多少层的加密细分,八叉树的最后一层节点始终能够表达出初始空间的全部信息。将八叉树应用于三维模型所在空间的分割细化中,通过不断分割节点产生子节点,提高体素模型精度,同时也保证了模型信息的完整性。
本文采用八叉树数据结构分割三维模型并存储模型信息,如图6所示,首先将模型的包围盒空间作为八叉树结构的根节点,然后模型空间被均匀分割为8个小空间,每个小空间都是八叉树根节点的子节点。此后,以上一次分割产生的小空间为父节点,将其均匀分割为8个更小的空间,作为该节点的8个子节点。不断重复细分过程,直到满足迭代过程的终止条件。本文采用最小体素尺寸作为八叉树结构分割的终止条件,即当最后一层八叉树节点体素的最小边长小于预设的体素阈值时,空间细分停止,基于八叉树三维模型体素化算法结束。
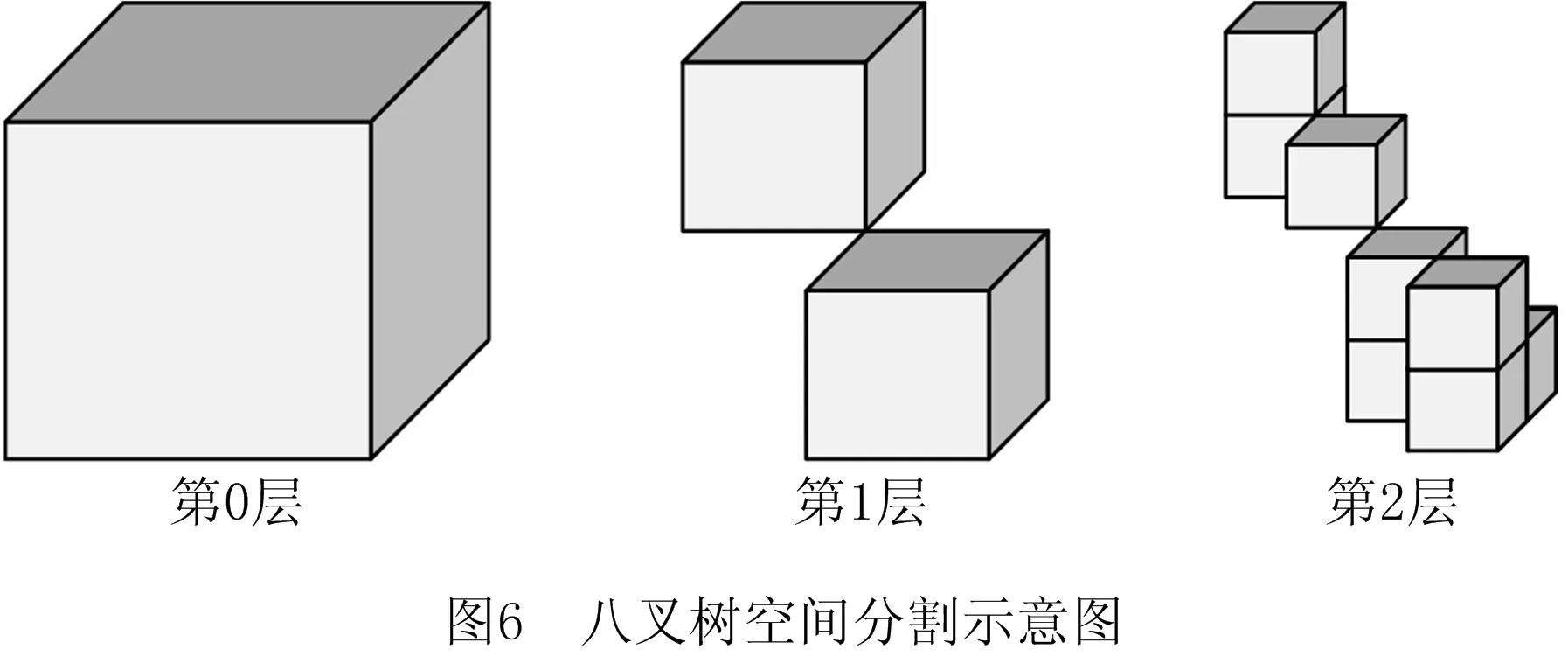
与完整八叉树结构不同,为了获得三维体素模型,需要对节点状态进行判断,保留满足要求的节点,删除不满足要求的节点。节点状态通过节点空间与三维模型点集的关系来判定,本文规定若节点空间内包含至少一个顶点,则表示该节点空间与模型为相交关系,因此将该节点标记为非空节点,否则标记为空节点。如图7所示,在基于八叉树结构的空间细分过程中,只有非空节点空间才需要继续分割,产生子节点,非空节点空间则被删除。
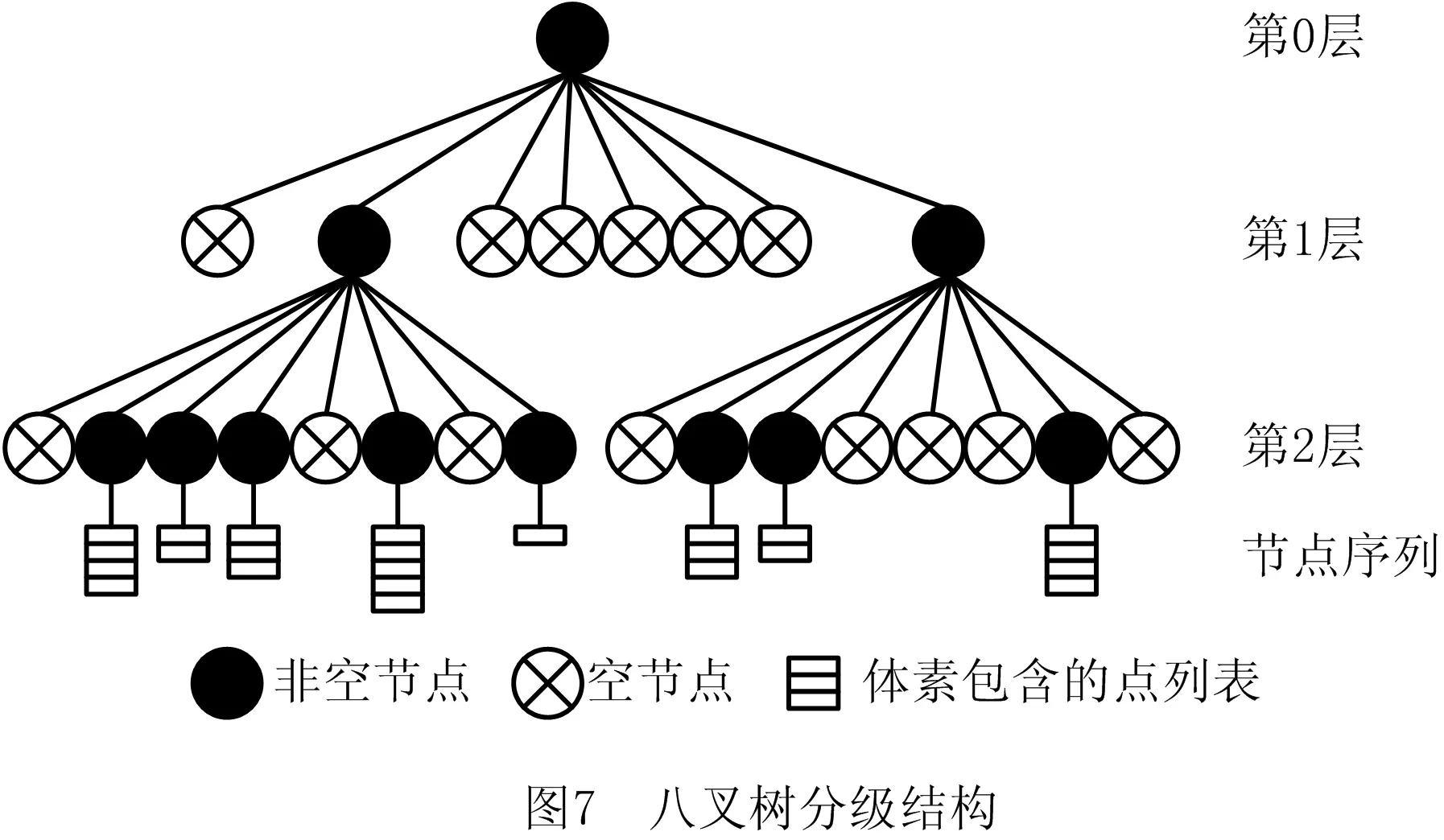
上述操作结束之后,将得到一棵多层次空间八叉树,模型的顶点信息全部存储在八叉树的非空节点中。提取八叉树最后一层的全部非空子节点,即得到三维模型对应的体素模型。
2.3 表面体素的线性细分
由于八叉树均匀分割空间的特性,八叉树中任意一层节点的对应体素的形状与模型包围盒形状均是相似的。如图8a所示为八叉树分割算法结束之后得到的叶节点体素,其长宽高分被设置为l、w、h,其中l>w>h。根据八叉树分割算法,叶节点体素中只有最短边满足算法终止条件,即w
此时若继续采用八叉树结构细分叶节点体素,体素还需八等分的次数可由式(3)~式(5)得出:

(3)
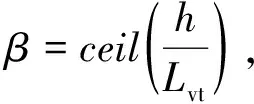
(4)
m=max(log2α,log2β)。
(5)
在图8中,假设八叉树叶节点体素三边l、w、h之比为4∶2∶1,则α=4,β=2,此时计算m=2,因此还需进行两次八叉树分割。不考虑细分后删除空节点的影响,记叶节点体素数量为M,继续采用八叉树细分后新的叶节点体素数量为M1,则M1可表示为:
M1=M×8m。
(6)
经过多级八叉树细分后,M很容易增长到十万甚至百万数量级,此时在M的基础上再进行m次的八叉树分割,M1将会以M为基数呈指数级增长,这将极大地增加内存负担,并降低算法效率。另外,经过多次八叉树分割,叶节点体素在较短边长上被分割至远小于体素阈值的长度,因此在该方向上可能出现体素误删的情况,造成体素模型精度损失。
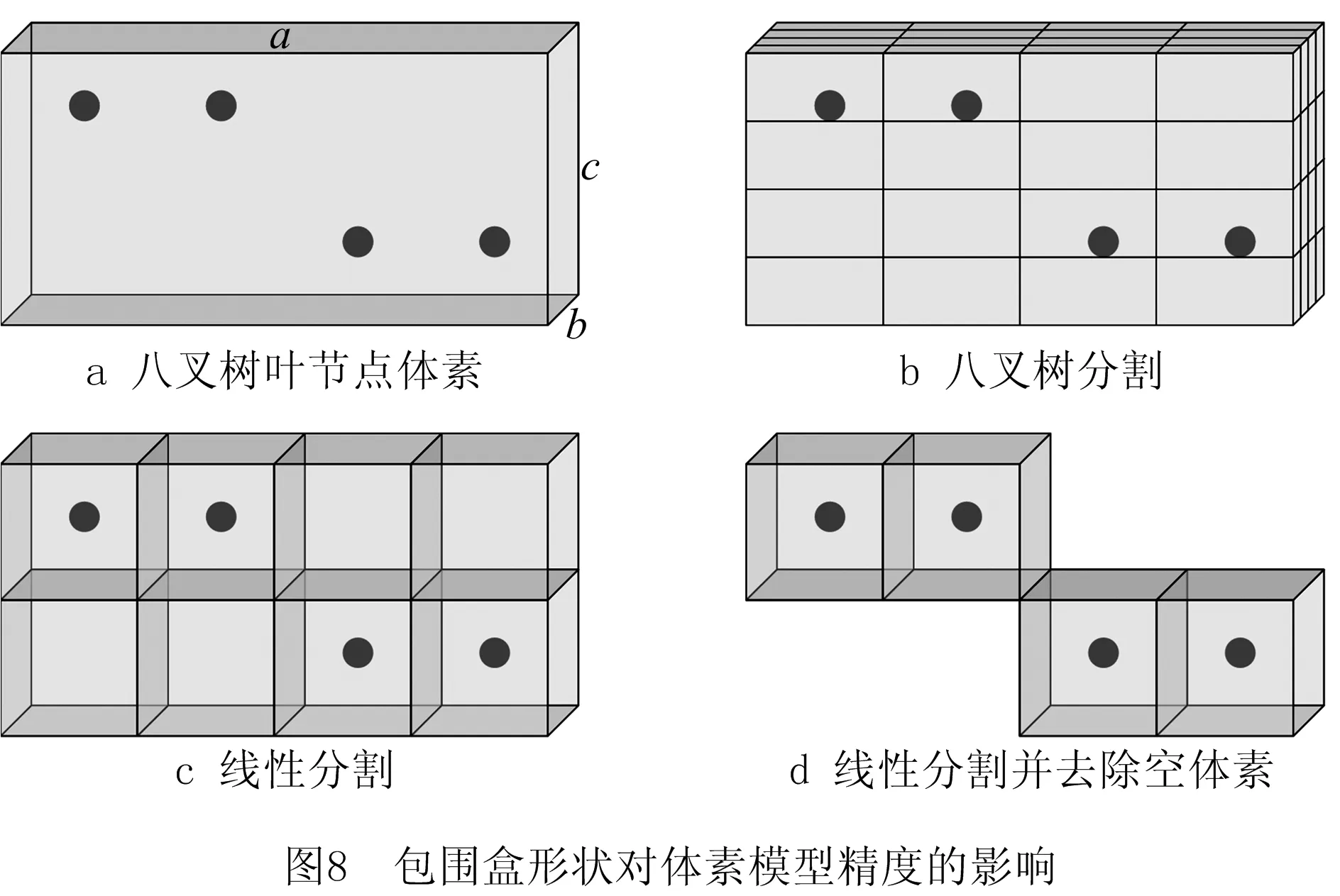
针对这一问题,本文在八叉树结构细分的基础上提出一种二次线性加密的体素细分算法,该方法在保证体素模型精度的前提下,尽量避免了不必要的体素分割,降低体素数量、提高算法效率。线性加密算法是指,对于经过八叉树加密后的叶节点体素,仅在其不满足体素阈值的方向上进行线性均匀细分,使得细分后体素三边均满足体素阈值的要求。
类似地,在不考虑空节点体素删除的影响下,采用线性细分后的体素数量M2可表示为:
M2=M×α×β。
(7)
通过比较式(6)和式(7)可知,M1始终大于M2,并且当l、h与Lvt的比值越大,两者的差距将会迅速增大。以图8所示情况为例,计算M1为64M,计算M2为8M,二者相差8倍。因此,二次线性加密方法在保证体素化精度的同时,有效地避免了不必要的体素分割,降低了体素数量。
对线性细分得到的新体素,判断其是否包含顶点信息,删除未包含顶点的空节点体素,保留的体素包含了全部顶点信息、并且三边均满足体素阈值。完成上述操作后,得到无颜色信息的表面体素模型。
2.4 表面体素颜色计算
在OBJ模型中,模型的颜色信息存储在三角面片顶点中,而体素模型的颜色信息则以体素为单位进行存储,并且在RGB颜色模型下,颜色信息可用一个三维向量表示,形如C(R, G, B)。因此,为实现彩色模型的表面体素化,还需完成模型颜色信息从三角面片顶点向体素的转换。在颜色信息的转换过程中,考虑到彩色模型表面颜色渐变的特点,可以简单地认为越靠近体素的顶点颜色对体素颜色的影响越大,因此本文选择体素包含的全部顶点作为体素颜色计算的参照点,并采用远小近大的原则计算体素颜色,如图9所示。
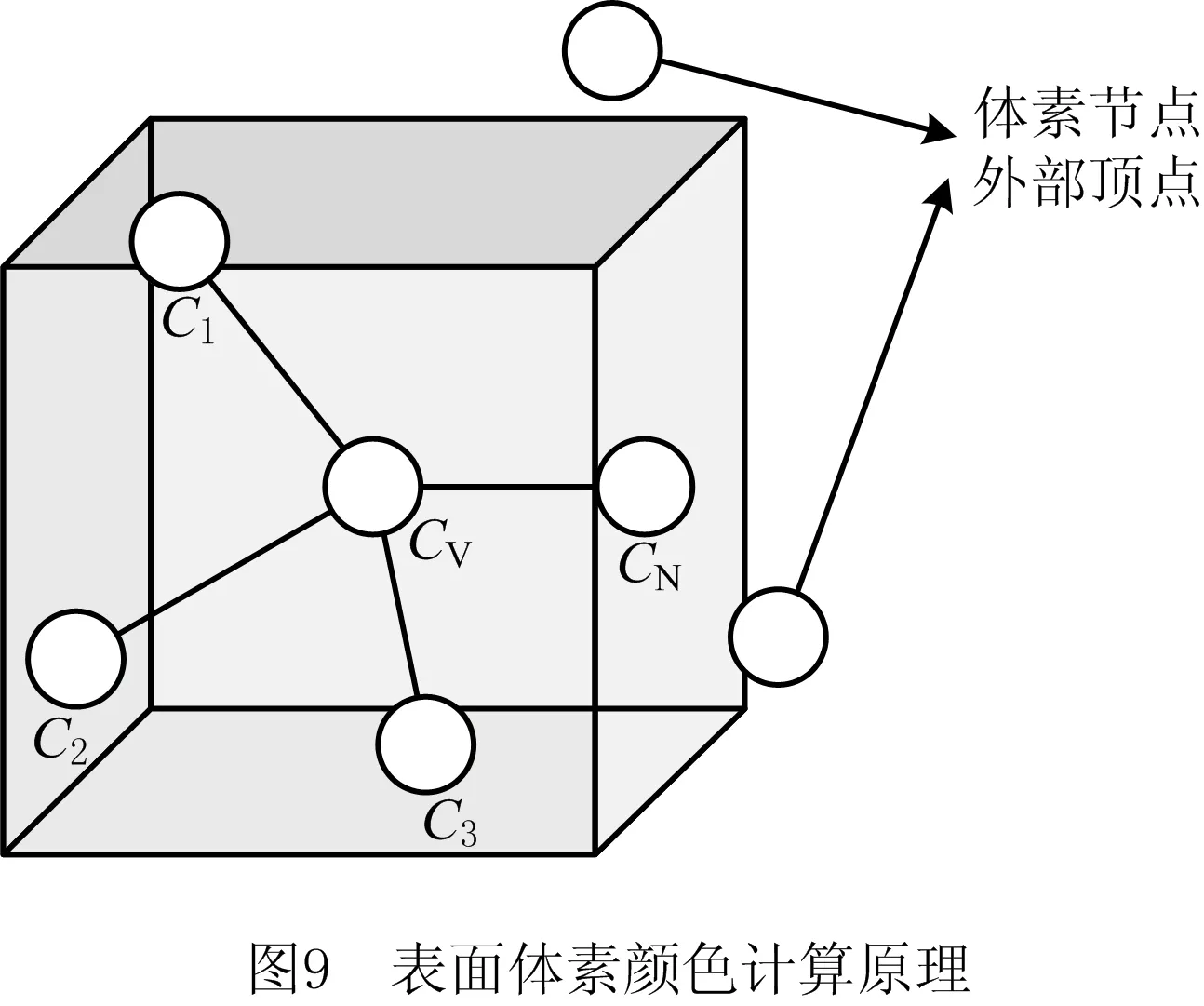
为衡量体素周围的顶点颜色对体素颜色的影响程度,本文提出一种基于距离的颜色影响因子λ,该影响因子的定义如下:
(8)
则体素的颜色可通过式(9)得到:
(9)
式中:Ci和Cv分别表示四顶点颜色和体素颜色,Si分别表示顶点与体素中心的距离。
3 算法验证
本文彩色模型表面体素化算法在Visual Studio环境下以C++语言编写应用软件,处理器为Intel(R)Core(TM)i5-8400 2.8 GHz,运行内存为8 GB。软件使用单线运行,以OpenGL编写的C++程序显示OBJ模型。本文选择CAD建模的法兰盘、校碑、豌豆射手、小黄人共4种彩色OBJ模型为主要实验对象,如图10所示,根据关键词完成模型数据的分割并分别存储在对应的数据容器中,即模型的数据重建,重建模型数据将作为后续体素化算法的初始数据。

3.1 算法效果
彩色模型表面体素化以彩色模型包围盒为八叉树根节点,通过不断细分并保留表面体素,去除非表面体素,逐步还原出模型的表面形状,如图11所示。图12展示了小黄人彩色模型表面体素多级细分过程,随着表面体素细分程序的执行,模型表面体素尺寸不断减小,表面模型模型精度不断提高。在OBJ模型三角面片细分足够密集的前提下,本文算法理论上可以通过不断细分表面体素,实现任何级别的表面体素精度。
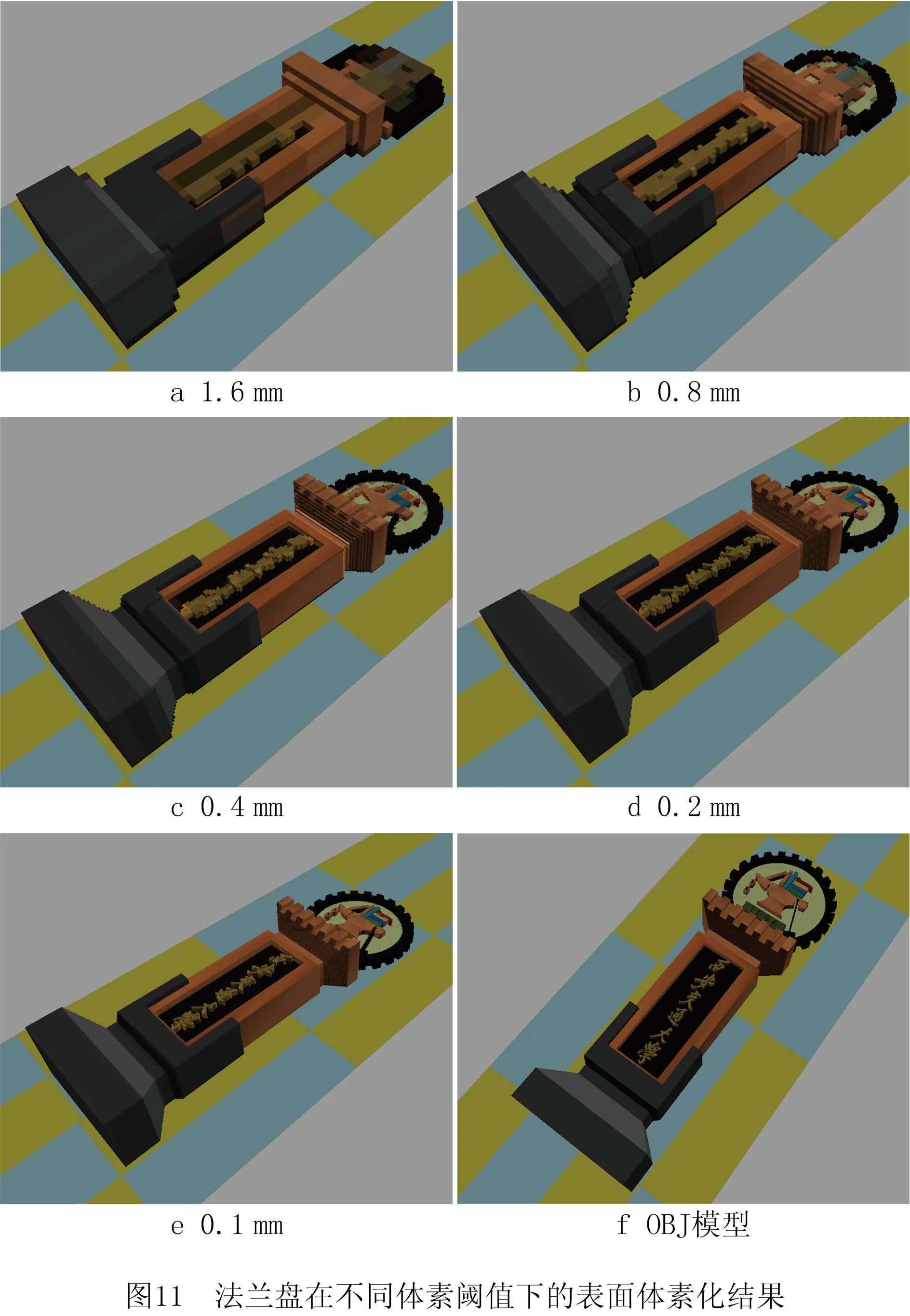
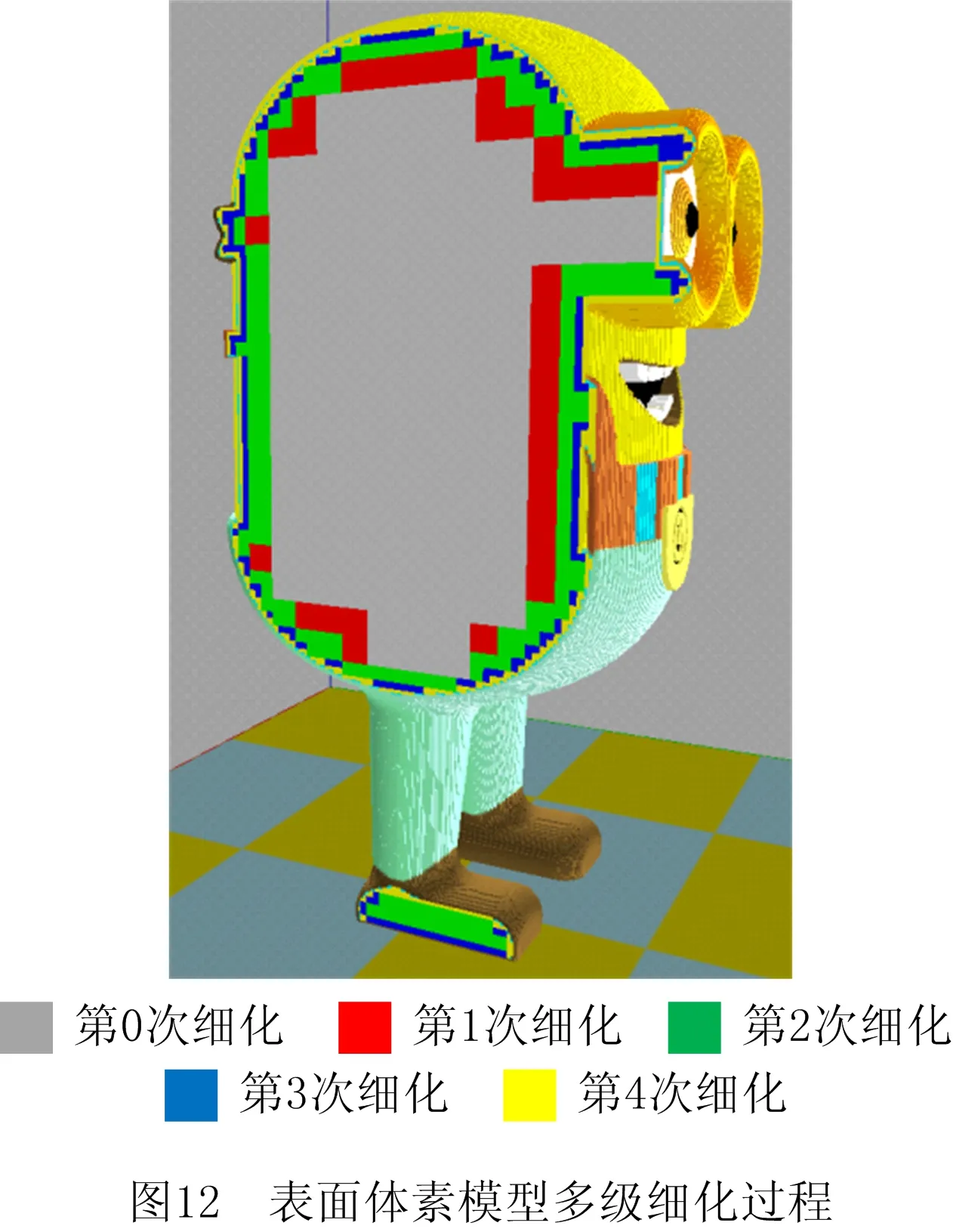
越高的体素模型精度要求越小的体素分割阈值,因此在不考虑其他影响因素的前提下,可以通过设置更小的体素阈值以实现更高的体素化精度。图12是校碑模型分别在1.6 mm、0.8 mm、0.4 mm、0.2 mm、0.1 mm和0.05 mm体素阈值下的表面体素化结果,如图12所示随着体素阈值设定值的减小,组成相应体素模型的体素尺寸逐渐减小,并且未包含三角顶点的表面体素不断被剔除,体素化精度不断提高,体素模型逐渐刻画出OBJ模型表面形状特征。
线性细分是在八叉树体素化表示的基础上,通过将体素进一步细分至接近立方体的体素类型并删除未包含点的体素,极大地提高体素模型的精度。图13为线性细分处理前后的体素模型效果图及局部细节图,从图中可以看出,经过线性细分处理,体素模型精度得到明显提升。在未经过线性细分之前,校碑体素模型中的体素形状与校碑包围盒是一致的,此时由于校碑包围盒尺寸的影响,体素模型中体素的大部分空间并未占据模型数据点,这导致体素模型细节特征十分模糊,如校碑模型上的文字部分。经过线性细分处理后,体素模型精度明显提高,校碑模型上的文字清晰度大大提高。

图14显示了法兰盘、校碑、豌豆射手、小黄人等OBJ彩色模型在0.1 mm体素阈值下的表面体素化结果。

值得注意的是,本文算法同样适用于“盖面”和“双面纸”等薄层结构[11],例如本文算法在处理上述模型中的豌豆射手的叶子结构时获得了不错的实验结果。
3.2 算法数据
为准确评价本文算法的性能,本文以法兰盘、校碑、豌豆射手、小黄人等4种彩色模型为实验对象,分别在1.6 mm、0.8 mm、0.4 mm、0.2 mm、0.1 mm体素阈值下,获得了相应的体素模型和算法详细数据,主要包括上述模型在不同体素阈值下的八叉树迭代次数、八叉树分割后表面体素数量、线性细分后表面体素数量和程序运行时间,具体如表2所示。通过表中数据可以得出以下结论:

表2 各彩色模型表面体素化的参数
(1)对于同一个彩色模型,随着体素阈值快速减小(负指数级),八叉树分割迭代次数的线性增加。
(2)同时,迭代次数的增加伴随着表面体素模型的体素数量和程序运行时间呈指数级快速增加,如图15和图16所示。
以豌豆射手模型为例,该模型体素化阈值从0.4 mm减小到0.2 mm时,经过附加一轮的体素分割细化,体素模型的精度仅提高一倍时,体素化模型的总体素数量增加为之前的3.69倍,程序运行时间增加为3.90倍。不断的细化迭代固然实现了更高精度的体素模型精度,但势必造成更大的数据存储压力和更低的算法效率。因此,在实际操作时,在模型精度满足要求的前提下,应尽可能地使用更大的体素阈值,以减小内存压力、提升算法效率。
(3)线性细分是本文算法提升体素化精度的重要过程,通过算法原理推断和实验数据分析均可以得到结论:输入模型包围盒长宽高中两两之比越是远离1,即模型越是细扁,体素模型线性细分对体素模型精度的提升越是明显。同时,模型越是细扁,线性细分之后表面体素数量增加越快。以校碑模型和豌豆射手模型为例,当体素阈值设为0.1 mm时,线性细分导致体素模型表面体素分别增加为103.49倍和5.14倍。因此,对于细扁模型,应同时考虑体素化精度和线性细分导致迅速增加的体素数量,选择合适的体素化阈值。
可以预知,在体素化精度和算法效率方面,本文提出的算法具有明显的优势。相比于文献[2]等提出的体素化方法,本文算法通过提前细分三角面片的方式,保证在较小体素阈值的情况下,彩色模型仍能够实现表面体素化,且体素化模型不会出现孔洞、裂缝等缺陷。文献[11]提出一种分割模型包围盒空间,通过标记细分采样点所在体素,以实现三维模型表面体素化。为更好地与本文算法进行对比,在相同的硬件条件下采用不同的体素化阈值,即不同的体素化分辨率,对同一模型进行体素化处理,本文算法与文献[11]产生的体素数量如表3所示。
表3中,本文算法的累计体素数量是指在多级八叉树分割和线性分割过程中产生的全部体素数量之和,文献[11]的总体体素数量是指模型在xyz三轴上等距分割产生的全部体素数量之和,二者均是各自算法中影响算法效率和数据量的重要参数。从表中可以看出,在较小体素化分辨率下,本文算法产生的累计体素数量略大于文献[11]产生的总体体素数量,但随着体素化分辨率增加,文献[11]的总体体素数量迅速超过本文算法的累计体素数量,且体素化分辨率越大,二者差距越大。

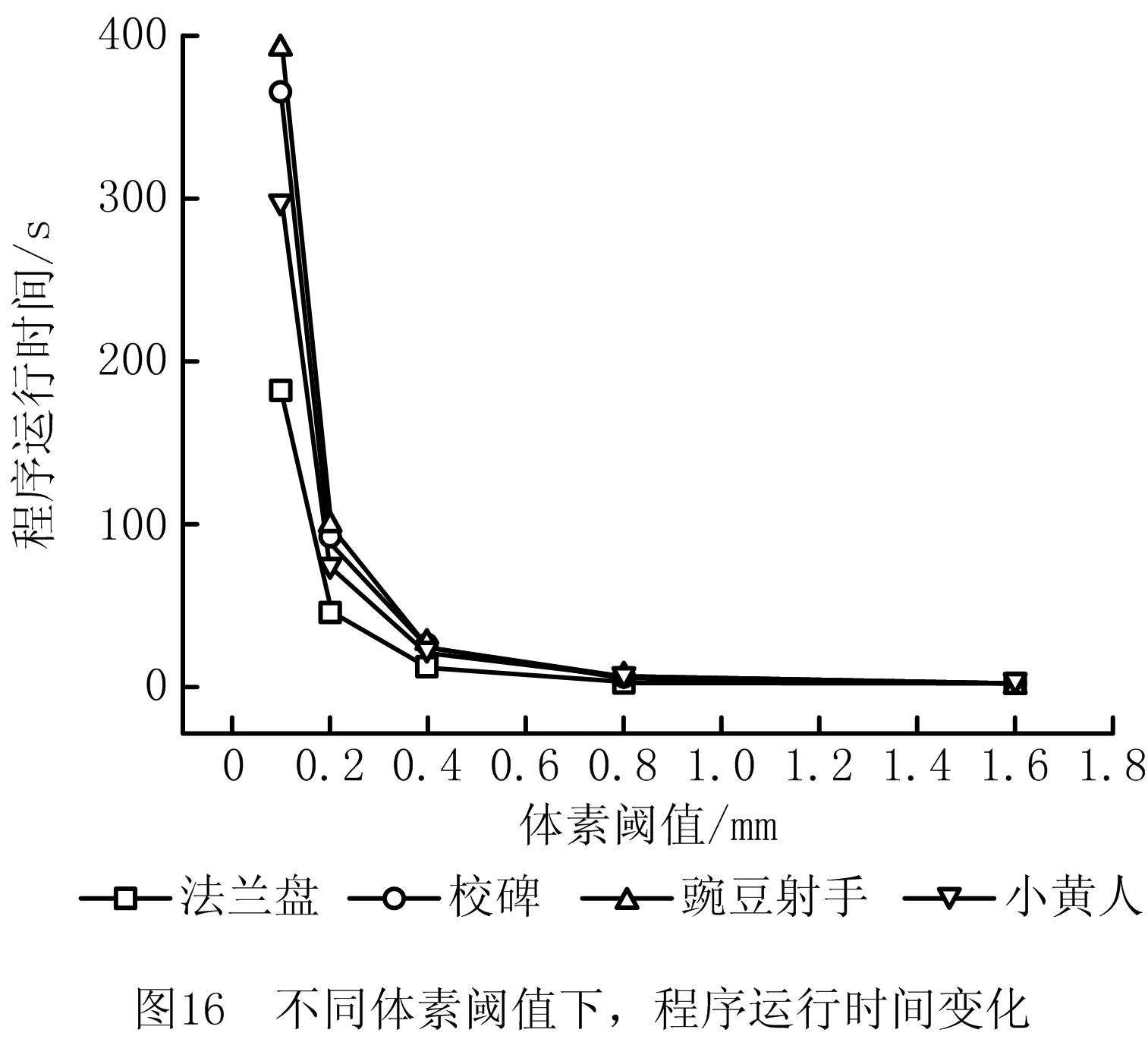

表3 本文算法与文献[11]算法数据比较
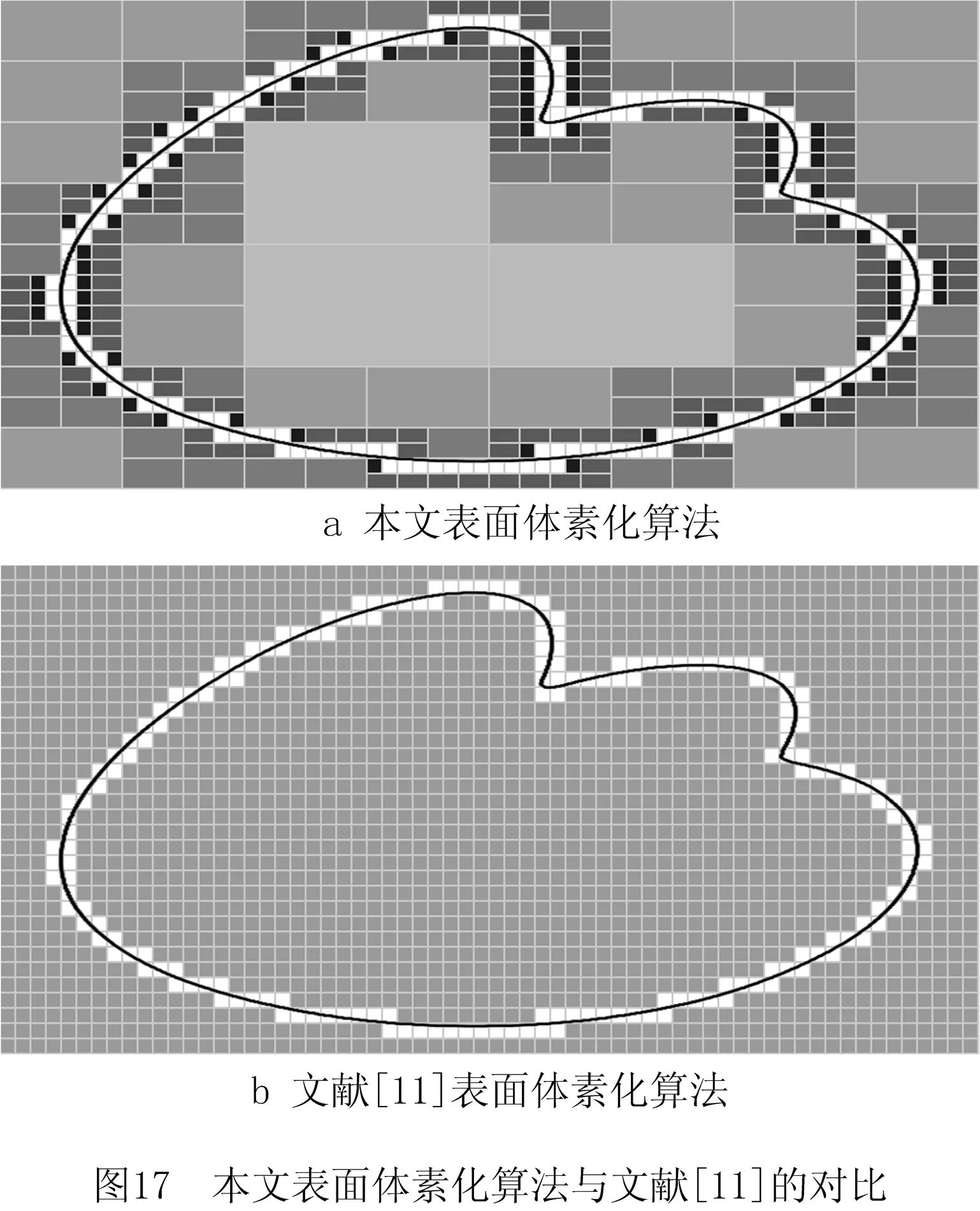
本文算法需要多级细分,且每一级细分之后都会生成新的体素表示,下一级体素表示总是上一级的子集,在空间上存在重复表示的情况,而文献[11]仅进行一次体素化分割,体素之间没有重复表示,因此在较小体素化分辨率下本文算法产生的累计体素数量会略大于文献[11]。本文采用八叉树结构+线性结构的方式逐级分割模型,如图17所示,每一级分割后,分割产生的新体素中只有与细分顶点有交集的部分才会被保留,被保留的部分将作为这一级分割的体素化表示,同时也自动成为下一级分割的父节点。相比于文献[11]的一次性分割至指定体素阈值,本文算法避免了各级分割中无用体素的存储和后续分割,因此算法产生的累计体素数量的增长速度得到有效控制,特别是在体素化分辨率越大的情况下,本文在该点上表现出越明显的优势。由表3可以看出,当体素阈值由0.2 mm减小为0.1 mm时,文献[11]产生的总体体素数量增长至上一级的8倍,而本文算法产生的累计体素数量仅增长至上一级的约4倍左右。
表3中,有效体素数量是指最终的体素化模型所包含的体素数量。理论上,在相同的体素化分辨率下,本文算法和文献[11]算法得到的体素模型的有效体素数量应该相等,表3中的实验数据证实了这一点。表3中,模型在体素阈值为1.6 mm和0.8 mm下进行体素化处理,本文算法和文献[11]算法产生的有效体素数量存在细微差异,这主要是因为在使用本文算法和文献[11]算法时,通过预设体素阈值计算最终体素模型分辨率,即模型在xyz三轴上的分割段数不一样导致的,如体素阈值为1.6mm时,本文算法的体素化分辨率是32×16×8,而文献[11]的体素化分辨率是25×13×7。
4 结束语
本文针对现有三维模型表面体素化过程容易出现表面破裂、体素模型精度低等问题,提出一种彩色模型表面体素化算法,该算法以OBJ彩色模型作为算法研究对象,将八叉树数据结构应用于模型分割过程。针对OBJ模型部分三角面片过大导致的表面体素模型出现破裂的现象,提出一种基于最大边长比的三角面片均匀细分算法,保证得到的体素模型能够完全封闭。针对现有表面体素化模型精度较低的现象,本文提出一种表面体素线性细分算法,大大提高了体素模型的精度。最后,本文使用了多个OBJ模型对上述算法进行了验证,实验结果表明,即是设定较小的体素分割阈值,算法仍然能够保证所得体素模型的全封闭性。
本文算法具有以下意义:
(1)充分利用了模型本身的三角面信息,间接通过三角面的线和面信息,实现三角面的顶点密化,结合八叉树分割的终止条件,严格保证了体素模型的表面封闭性。
(2)结合模型包围盒的形状,对八叉树结构中的体素线性细分分割,使体素的形状趋向于正方体,细化体素尺寸,极大地提高了体素模型的精度。
(3)本文算法同样适用于薄层结构的表面体素化,这是基于模型轮廓的体素化算法所不能实现的功能。
(4)在体素级增材制造领域,基于本文算法得到的彩色体素模型,材质分布定义和色彩管理将变得十分容易,如定义复杂的功能梯度材料的分布和彩色模型3D打印过程中的色彩管理。此外,体素模型经过简单的切片和填充过程,即可得到彩色增材制造所需的切片文件。切片文件将会决定在何处喷射何种成型材料(PolyJet技术)或者何种类型的粘结剂(3DP技术)。
在不考虑三角面片近似造成的原始三维模型精度损失外,本文算法可以通过减小体素阈值得到任意精度的体素化模型,然而这也将导致巨大的体素数量和时间成本。因此,下一步研究主要集中在通过将满足要求的邻近体素合并或者在体素分割时不处理无需分割的体素,以实现更高的体素化效率和更小的体素数量。如,此处“满足要求的邻近体素”可以定义为空间坐标之一相同并且可以合并为新体素的邻近体素,“无需分割的体素”则可以是最后一次八叉树分割后,所得子节点全部被保留的父体素。
另外,本文的体素化算法仅处理模型的表面形状和色彩信息,然而在聚合物喷射成型工艺的众多应用场景中,存在模型表面体素化+内部体素化的需求,即模型实体体素化,如复杂功能梯度材料模型、半透明彩色模型3D打印应用中,模型内部的材质或颜色定义是不可或缺的。因此,如何高效准确地实现三维模型实体体素化也是下一步的研究方向之一。
