基于单胞模型的三维四向编织复合材料力学性能研究

苏蕴荃 陈昊 侯传涛 刘培硕 霍宁飞

（1 北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076；2 北京强度环境研究所，北京 100076）

0 引言

作为复合材料领域中的新兴方向，三维编织复合材料因其良好的力学性能近年来得到了快速发展。三维编织复合材料是一种新型结构化编织复合材料，其内部纱线构成了高度整体化的空间互锁网络结构，材料整体连续分布，因此从根本上克服了传统层合复合材料易分层、开裂和抗冲击性能差等缺点，同时还具有较高的比强度和比刚度、抗冲击韧性、耐烧蚀性及结构可设计性等优点[1]，因此在航空航天、生物医疗、体育器械、建筑等诸多领域都得到了广泛应用[2,3]。

由于三维编织复合材料内部的细观结构具有几何周期性，因此利用代表性体积单元（RVE）对三维编织复合材料的力学性能进行研究和预测是一种常用且有效的手段。国内外的专家学者针对此研究方向开展了大量的研究。Ko[4]于1982年首次提出了能够反映材料编织成型工艺的一种单胞模型，该模型包含了六面体沿对角线方向的四条直纤维束；Yang等[5]根据纤维束的空间走向，以经典层合板理论为依据提出了“纤维倾斜模型”；吴德隆等[6]针对以四步法为基础的三维五向编织复合材料提出了基元单胞、面单胞和柱单胞的三胞模型；Li等[7]基于三维四向直角编织复合材料的微观结构，提出了参数化的有限元模型，模拟了编织纱线的空间结构并考虑了纱线的横截面变形和表面接触，研究了编织角和内部编织角之间的关系；Hao等[8]通过分析纱线的运动规律，提出了一种用于预测三维四向编织复合材料杆结构的单胞模型。Xu等[9]考虑了纱线畸变及壳芯结构特征，通过建立一种多单元模型分析预测了三维编织复合材料的弹性性能。在实际应用中，抗冲击性能是三维编织复合材料相对于传统层合复合材料的主要优势，而强度问题则是工程结构设计中最为关心的问题。在三维编织复合材料冲击性能方面，Zhou等[10]建立了三维编织复合材料管道的细观有限元模型，模拟了该模型在承受横向高速冲击时的变形行为；其后他们[11]又建立了三维编织复合材料工字梁的细观有限元模型，并模拟了工字梁结构在改进的霍普金森压杆冲击下的应力分布和失效过程；Zhang等[12]建立了考虑三维率相关本构模型的三胞元模型，利用该模型评估了三维编织复合材料高速冲击下的侵彻过程。在强度研究方面，孙慧玉等[13]采用Tsai-Wu多项式失效准则，以修正的经典层合板模型为基础，研究了三维编织复合材料的强度问题。Zuo等[14]先是应用Tsai-Wu强度准则的二阶表现形式，给出了计算三维编织复合材料纵向拉伸强度的一种新的方法。又基于单向复合材料的拉伸统计强度的统计学模型[15]，提出了一种新的计算三维编织复合材料拉伸统计强度的方法，并通过数值分析结果验证了该方法的可行性。Zeng等[16]采用Tsai-Wu准则和Mises准则分别作为纤维和基体失效判据，用刚度折减法对单胞模型进行了损伤分析。研究并预测RVE的细观力学性能对于三维编织复合材料整体力学性能的研究具有重要意义。目前，利用有限元仿真手段对三维编织复合材料细观模型抗冲击性能进行研究的报道尚不多见，而关于三维编织复合材料细观模型强度问题的研究也处于探索阶段。因此，本文从三维编织复合材料的细观结构出发，利用有限元分析软件建立了三维四向编织复合材料的单胞模型，然后针对三维四向编织复合材料单胞的静力学性能、抗冲击性能及强度分别进行了研究和预测。

1 三维四向编织复合材料单胞模型的建立

1.1 三维编织复合材料的制造工艺

三维编织复合材料由纤维和基体组成，制作三维编织复合材料的第一步是通过三维编织技术将高性能纤维编织成预先设计好的预制件。三维编织技术指的是使编织纱在三维空间中相互交织或交叉在一起，形成一个不分层的整体结构预制件的方法（图1）。目前制作整体三维编织复合材料预制件的方法主要有二步编织法和四步编织法。三维四向编织预制件就是通过四步1×1编织程序制作而成的。在将预制件制作好后，将其作为增强体，通过特定的成型工艺[17]，与基体材料进行固化形成整体三维编织复合材料。常见的基体材料有树脂基、陶瓷基、金属基、碳基等[18]。本文研究对象是三维编织复合材料中最常见的碳纤维/环氧树脂复合材料，其中碳纤维牌号是T300。通常认为碳纤维是线弹性、横观各向同性材料，而环氧树脂是线弹性、各向同性材料。T300碳纤维和环氧树脂的部分力学性能参数[19]见表1。

表1 T 300碳纤维和环氧树脂部分材料性能参数Table 1 Several material parameters of carbon fiber T300and epoxy resin

图1 三维编织工艺示意图[7]Fig.1 Schematic diagram of 3D braiding process

1.2 单胞模型的建立

由于内部结构化特征，三维编织复合材料具有优良的可设计性。根据内部纱线的走向不同，三维编织复合材料可分为三维四向、三维五向、三维六向、三维七向等[20]多种空间结构类型。本文针对常见的三维四向编织复合材料建立了内部单胞模型（图2）。后面以图2中的正方体单胞为例，详述三维四向编织复合材料内部单胞模型的建立方法。三维四向编织复合材料单胞内部的纤维束走向一共有四个方向。1方向上有七根纤维束，其中一根是横贯整个正方体单胞内部的体对角线，其余六根位于正方体单胞的其他六个角点上。2、3、4方向上分别有四根纤维束。整个单胞内部一共有十九根不同的纤维束（图3）。

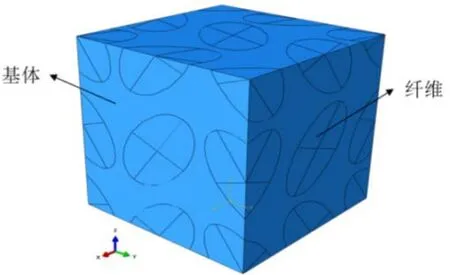
图2 三维四向编织复合材料正方体单胞模型Fig.2 The cubic unit cell of 3D four-directional braided composites

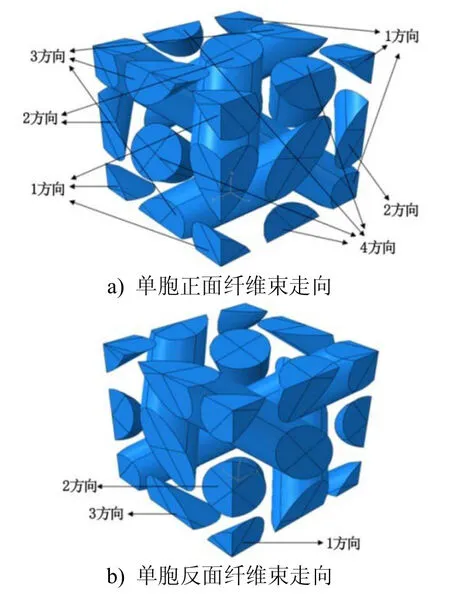
图3 正方体单胞内部的纤维束走向Fig.3 The directions of fiber bundles in the cubic unit cell

纤维体积含量和编织角是三维编织复合材料的两个主要编织工艺参数，也是决定三维编织复合材料单胞构型的几何参数。这里纤维体积含量指的是纤维束体积占整个三维编织复合材料体积的百分数，而编织角指的是纤维束与编织方向之间的夹角。对于三维四向编织复合材料而言，其纤维体积分数Vf可表示为

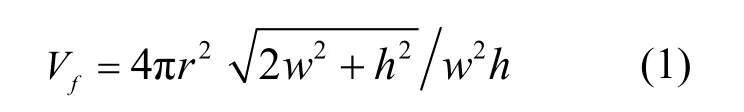
其中r表示纤维束的半径，π为圆周率，w和h分别表示单胞底面的宽度和单胞的高度。编织角.则可表示为

在正方体单胞中，单胞底面的宽度和单胞的高度相等，于是可以得到其编织角a= 54.74°，同时公式（1）可简化为

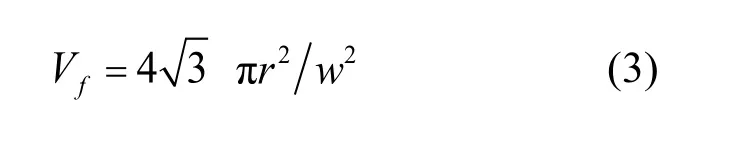
因此，当已知纤维束半径和纤维体积含量时就可以得到正方体单胞的尺寸参数了。这里纤维束半径取r= 0.5mm，纤维体积含量Vf= 54%，于是得到正方体单胞的边长w=h= 3.174mm。

结合纤维、基体的力学性能参数和单胞的几何参数，即可利用有限元分析软件ABAQUS创建出三维四向编织复合材料的单胞模型了。

2 三维四向编织复合材料单胞力学性能分析

2.1 静力学性能分析

通过细观单胞模型预测材料整体的力学性能是三维编织复合材料研究中的一个重要方法。三维编织复合材料具有横观各向同性的本构关系，而纤维体积含量和编织角的变化都会导致其弹性模量的变化。下面以编织角为20°，纤维体积含量为40%的单胞为例来计算它的弹性模量，如图4所示。

图4中z方向为单胞的编织方向，在ABAQUS中通过对z方向施加小位移载荷，并输出加载面上预先设置好的参考点的反力和位移，即可计算出图4中编织角为20°，纤维体积含量40%的三维四向编织复合材料单胞沿编织方向的弹性模量。从ABAQUS中按分析步输出的反力和位移数据见表2。

图4 编织角20°、纤维体积含量40%的单胞Fig.4 The unit cell with braiding angle of 20° and fiber volume fraction of 40%

表2 参考点反力和位移Table 2 The reaction forces and displacements of the reference point

由于纤维体积含量和编织角已知，因此根据式(1)～(3)可以得到：单胞底面的宽度w=2.89mm，单胞高度h=11.23mm，单胞的横截面积S=8.35mm2。再根据表2中的位移和反力数据求得单胞在对应载荷下的应力应变，即可得到三维四向编织复合材料单胞沿编织方向的弹性模量。同样地，也可以得到单胞x方向和y方向的弹性模量，结果见表3。由表3中的结果可以看出，单胞沿编织方向的弹性模量最大，另外两个方向的弹性模量则基本相同，这是由于三维编织复合材料是横观各向同性材料。

表3 编织角为20°纤维体积含量为40%的单胞三个方向的弹性模量Table3 The elastic moduli of the unit cell with braiding angle of 20° and fiber volume fraction of 40% in three orthogonal directions

2.2 抗冲击性能分析

三维编织复合材料因其结构特点而具有十分良好的抗冲击性能。前面已经提到，纤维体积含量和编织角是三维编织复合材料的两个主要内部构型参数，因此它们可能对三维编织复合材料的抗冲击性能有重要影响。在实际应用中，三维编织复合材料主要承受沿编织方向的冲击载荷作用，因此这里只针对三维编织复合材料单胞沿编织方向的抗冲击性能进行研究。

本文对三维四向编织复合材料单胞的冲击过程模拟在ABAQUS/Explicit模块下进行，由于主要针对细观单胞模型，因此暂未考虑冲击中的阻尼效应。为保证冲击速度不变，对所有单胞在相同的冲击时间（10-7s）内统一施加100MPa的冲击载荷。通过获取冲击加载面上预先设置好的参考点位移，可得到单胞沿编织方向的应变，从而得到三维编织复合材料单胞在冲击载荷下的应变-冲击时间变化关系。

图5首先给出了单胞在承受冲击荷载的过程中，某一横截面上连续四个分析步的Mises应力分布情况，从图中可以看出，在承受冲击荷载时，三维四向编织复合材料单胞内的应力波传播方式主要是沿着纤维束进行的。

图5 单胞横截面上的Mises应力分布Fig.5 Mises stress distribution on the cross section of unit cell

为研究编织角对三维编织复合材料单胞抗冲击性能的影响规律，在相同纤维体积含量（40%）、相同冲击速度的情况下，在ABAQUS中分别建立编织角为20°、30°、40°的单胞模型，然后对它们进行冲击过程模拟，应变-冲击时间响应曲线如图6所示。

由图6中的结果可以看出，在整个冲击过程中，不同编织角单胞的应变-冲击时间响应曲线在变化规律上基本一致，但在抗冲击性能上则存在着较为显著的差异，可见在纤维体积含量一定的情况下，编织角对三维四向编织复合材料单胞的抗冲击性能是有很大影响的，编织角越小，对于冲击载荷的响应越稳定，抗冲击性能越好。

图6 三种不同编织角单胞的应变-冲击时间响应曲线Fig.6 Strain-time curves of unit cell with three different braiding angles

同样地，为研究纤维体积含量对三维四向编织复合材料单胞抗冲击性能的影响规律，在相同编织角（40°）、相同冲击速度的情况下，在ABAQUS中分别建立纤维体积含量为30%、40%、50%的单胞模型，然后对它们进行冲击模拟，应变-冲击时间响应曲线如图7所示。

图7 不同纤维体积含量单胞的应变-冲击时间响应曲线Fig.7 Strain-time curves of unit cell with three different fiber volume fractions

由图7中的结果可以看出，在整个冲击过程中，不同纤维体积含量单胞的应变-冲击时间响应曲线的变化规律基本一致，且应变响应的差距较小。由此可见，在编织角一定的条件下，纤维体积含量对于三维四向编织复合材料单胞抗冲击性能的影响相对较小。

3 三维四向编织复合材料单胞强度分析

3.1 扩展有限元方法

扩展有限元方法（eXtended Finite E lement Method，XFEM）是由美国西北大学的Belytschko和Black[21]首先提出的一种计算裂纹等非连续界面问题的新方法。近年来扩展有限元方法不断发展和完善，已经逐渐成为了一种处理断裂、局部变形和非连续场等复杂力学问题的新方法，在航天航空、土木工程以及材料科学等很多领域都得到了广泛应用。由于扩展有限元方法在处理非线性材料、非线性几何分析以及非连续场力学问题上具有显著优势，因此本文采用这种方法对三维四向编织复合材料的单胞进行强度分析。

对三维编织复合材料单胞进行强度分析是研究和预测三维编织复合材料整体强度问题的一种有效手段。由于纤维体积含量和编织角也是影响三维编织复合材料强度的重要参数，因此本文在不考虑夹杂、界面、缺陷等因素的理想情况下，采用Mises应力作为强度表征，针对纤维体积含量和编织角对于三维四向编织复合材料单胞强度性能的影响规律进行了研究。

由于三维编织复合材料是横观各向同性的，所以材料沿编织方向的强度与其他方向的强度不同。这里只针对其受力的主要方向即编织方向的强度进行研究。

3.2 纤维体积含量对三维四向编织复合材料单胞强度的影响

为研究纤维体积含量对三维四向编织复合材料单胞强度的影响规律，在编织角保持40°不变的情况下，在ABAQUS中分别建立纤维体积含量为30%、35%、40%、45%、50%的单胞模型，然后对它们进行强度分析。

本文对三维四向编织复合材料单胞的强度分析在ABAQUS/Standard模块下进行，在ABAQUS中使用扩展有限元的优势之一就是不需要预设裂纹的位置。为了能够看到裂纹的扩展过程，在创建的场输出中将STATUSXFEM选项输出，即可跟踪到XFEM单元的状态，从而观察到裂纹的整个扩展过程。单胞断裂后的裂纹形态及Mises应力分布情况如图8所示。

图8 利用XFEM得到的断裂后单胞Fig.8 The cracked unit cell simulated by XFEM

与计算单胞弹性模量的方法相同，输出加载面上某一参考点的反力以求得能使单胞失效破坏的最大应力。将单胞的下底面沿z方向的自由度和围绕x、y、z轴转动的自由度全部固定，并在该面任意选取两个点固定住其全部六个自由度，以使得单胞在整个受力过程中的位置不发生移动。在单胞的上底面施加一定的位移载荷，使得单胞处于单轴拉伸的应力状态。

为了得到更准确的强度值，对不同纤维体积含量的单胞分别施加0.2mm、0.3mm、0.4mm的位移载荷，依次得到其破坏时的最大应力，然后取平均值，从而得到纤维体积含量为30%、35%、40%、45%、50%的单胞的强度极限，结果如图9所示。可以明显看出，在编织角一定的条件下，纤维体积含量越高，三维四向编织复合材料单胞的强度越大。

图9 纤维体积含量对单胞抗拉强度的影响Fig.9 The influence of fiber volume fraction on the tensile strength of unit cell

3.3 编织角对三维四向编织复合材料单胞强度的影响

为研究编织角对三维四向编织复合材料单胞强度的影响，在纤维体积含量保持40%不变的情况下，在ABAQUS中分别建立编织角为20°、25°、30°、35°、40°的单胞模型，然后对它们进行强度分析。为了得到材料更准确的强度值，对不同编织角的单胞分别施加0.2mm、0.3mm、0.4mm的位移载荷，依次得到其破坏时的最大应力，然后取平均值，从而得到各个单胞的强度极限，从而得到编织角为20°、25°、30°、35°、40°的单胞的强度极限，结果如图10所示。可以明显看出，在纤维体积含量一定的条件下，编织角越大，三维四向编织复合材料单胞的强度就越小。

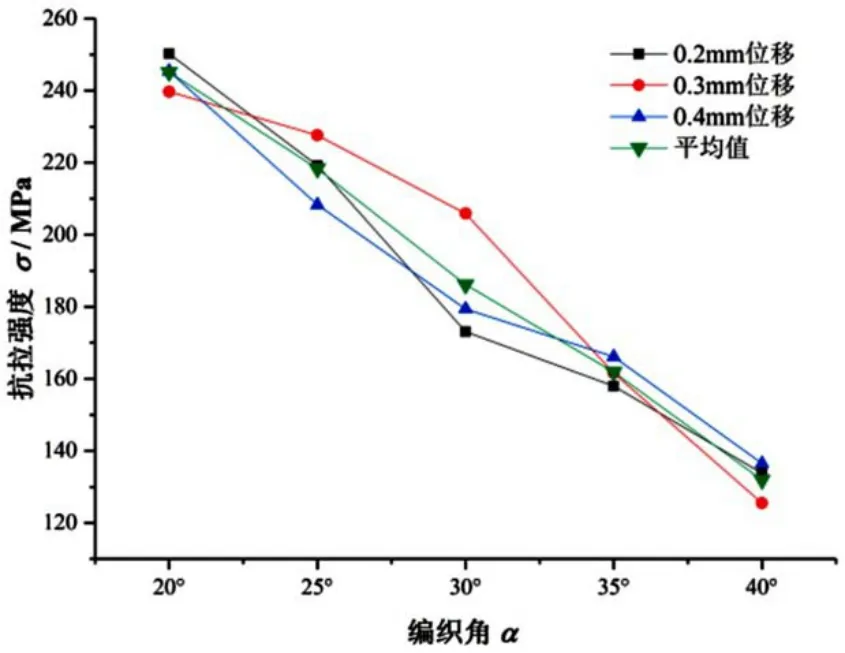
图10 编织角对单胞抗拉强度的影响Fig.10 The influence of braiding angle on the tensile strength of unit cell

4 结论

本文采用数值模拟研究方法，利用有限元分析软件建立了三维四向编织复合材料的单胞模型，从细观力学角度对其静力学性能、抗冲击性能及强度进行了数值模拟和分析，得到了以下结论：

1）通过对三维四向编织复合材料的单胞模型进行单轴拉伸数值模拟，计算得到了单胞三个正交方向的弹性模量，结果显示单胞沿编织方向的弹性模量最大，另外两个方向的弹性模量较小且基本相同。

2）针对三维四向编织复合材料单胞进行了冲击过程数值模拟，得到了单胞的应变-冲击时间响应曲线，分析了应变随时间的变化规律，并分别研究了纤维体积含量和编织角对三维四向编织复合材料单胞抗冲击性能的影响规律，结果发现编织角对其抗冲击性能的影响较大，编织角越小，单胞对于冲击载荷的响应越稳定，抗冲击性能就越好；而在编织角一定的条件下，纤维体积含量对于三维四向编织复合材料单胞抗冲击性能的影响相对较小。

3）利用扩展有限元方法对三维四向编织复合材料单胞进行了强度分析，研究了在纤维和基体材料确定以及不考虑杂质、缺陷等因素的理想情况下，纤维体积含量和编织角对三维四向编织复合材料单胞强度性能的影响规律。结果显示，在编织角一定的条件下，纤维体积含量越高，三维四向编织复合材料单胞的强度越高；在纤维体积含量一定的条件下，编织角越大，三维四向编织复合材料单胞的强度就越小。