用几何拼装法推导拉普拉斯算符在几种坐标系中的表达式

李品钧

(湛江幼儿师范专科学校信息科学系，广东 湛江 524037)

拉普拉斯算符是物理学中较为常见的一种算符，在本、专科物理学教材中即已常见[1-5]。其在直角坐标系中的定义式为

(1)

在特定的问题中，为了数学处理上的方便，常需将其变换到不同的参考系。文献[6]、[7]利用正交曲面坐标系的特性进行了简洁优美的计算，其法要求学习者对数理方法有较深厚的基础功底和较良好的空间想象力。文献[8]用复合函数求导的方法直接在上述两个坐标系中变换，工作量较为繁复。基于上述种种原因，许多初学者在其他坐标系中使用该算符时，都是采用查手册的方式直接使用。然而，从下面介绍的变换方法中可以看出，在将拉普拉斯算符从直角坐标系变换到其他坐标系的推导过程中，可以获得较多的数学图像体验。其次，若选择适当的技巧，较大幅度地减少计算量也是可能的。本文从不同坐标系之间的几何关系入手，推导拉普拉斯算符在极坐标、柱坐标和球坐标中的表达式，以期让初学者获得较为简洁形象的图像体验。

图1 x、y、ρ、φ关系图

1 拉普拉斯算符在极坐标中的表达式

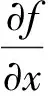
(2)

(3)

同时

(4)

于是有

(5)

将式(3)、式(5)代入式(2)便得

(6)

即

(6*)

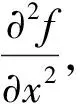
(7)

(8)

将式(3)、(5)、(6)诸式代入式(8)并整理得

(9)

即

(9*)

同法可得

最后，将式(9*)、式(11)相加，即得

(12)

上式右边即为拉普拉斯算符在极坐标中的表达式。

2 拉普拉斯算符在柱坐标中的表达式

(13)

上式右边即为拉普拉斯算符在柱坐标系中的表达式。

3 拉普拉斯算符在球坐标系中的表达式

图2反映了直角坐标系、极坐标系、柱坐标系和球坐标系几种坐标系之间自变量之间的几何关系。图中ρ是r在xOy平面上的投影。即

ρ=rsinθ

(14)

图2 x、y、z、ρ、φ、r、θ关系图

由前面的讨论可知，当自变量从x、y变换为ρ、φ时，式(10)、式(12)成立。注意到，在zOρ平面上，自变量z、ρ与r、θ之间的对应关系与xOy平面上自变量x、y与ρ、φ之间的对应关系相同。也就是说，球坐标系(r，θ，φ)可看成是两个极坐标(ρ，φ)和(r，θ)拼装而成。这样，将式(10)、式(12)中的x、y、ρ、φ换为z、ρ、r、θ，等式仍然成立，即

将式(16)代入式(13)左边并整理，可得

(17)

将(14)、(15)两式代入式(17)右边，得到拉普拉斯算符在球坐标中的表达式：

(18)

稍加整理即可得到其常用形式

(19)

4 结语

利用坐标系之间的几何关系，可以直观地求解两坐标系变量之间的微分关系，柱坐标可以拆分成极坐标和z轴，球坐标可以拆分成为两个极坐标。这样，复杂的计算就可化为简单的拆分和组合，极大地减少了计算量。