物理概念“熵”的多维剖析

田景华 袁海泉

(1苏州大学能源学院； 2能源与材料创新研究院； 3苏州纳米科技协同创新中心； 4苏州大学物理学院, 江苏 苏州 215006)

物理概念熵是非常抽象的，学生很难理解、消化和吸收。本文拟从热力学第二定律出发，引出熵概念的起源、发展和泛化，并从物理和化学两个不同的角度，通过大量的生活中常见的现象和简单的数学模型对熵的概念、含义和本质进行讨论和分析，以期更好地促进学生对这个抽象概念的认识与理解。

1 熵的起源

熵的概念是由德国物理学家克劳修斯于1865年提出的，在希腊语中意为“内在”，即“一个系统内在性质的改变”，公式中一般记为S。1923年，德国科学家普朗克(Plank)来中国讲学用到entropy这个词，胡刚复教授翻译时，把“商”字加火旁来意译“entropy”这个字，创造了“熵”字，即熵变dS是δQ与T(温度)的商数[1]。

根据热力学第一定律，我们知道热量可以从一个物体传递到另一个物体，也可以与机械能或其他能量互相转换，但是在转换过程中，能量的总值是保持不变的。热力学第一定律描述了自然界能量守恒的本质，事实上一切实际的热力学过程都必须满足热力学第一定律。然而在实际过程中，一切实际的宏观过程都是按一定方向进行的。大学物理课程一般会从热机、制冷机的循环过程、热机效率、制冷系数出发，引出可逆过程和不可逆过程的概念，并重点讨论几个经典的不可逆过程。它们是功热转换过程的不可逆性、热传导过程的不可逆性和气体绝热自由膨胀过程的不可逆性。在热机效率不可能达到100%的事实基础上，给出了热力学第二定律的开尔文(Kelvin)叙述：从单一热库吸收的热量全部用来完成等量的功而对外不产生影响是不可能的，也即第二类永动机是无法实现的。克劳修斯(Clausius)将热力学第二定律描述为：热量不能自动地从低温物体流向高温物体，即一台制冷机连续不断地把热量从低温物体输送给高温物体而不产生其他效应是不可能的[2]。

但开尔文、克劳修斯等人对热力学第二定律的表述都只是定性的描述, 不能定量说明过程发生的可能性及实际发生过程的不可逆程度。因此，克劳修斯在1865年首先提出熵的概念。克劳修斯将一个系统从一个平衡态经历了一个无限小的准静态过程变化到另一个平衡态，系统在两个平衡态之间熵的增量dS定义为传递的热量δQ除以系统的热力学温度T，即：

dS=δQ/T

(1)

从上面的定义可知，这里并没有直接给出熵S的定义，而是给出了熵变的计算方法，因此要理解熵的物理意义只能通过其在不同场合的使用中所表达的含义去体会。但由此熵成为热力学系统的基本状态函数，由它导出了热力学第二定律的数学表达式, 并形成了对两种不同状态过程发生可能性的定量判据。在引入熵的基础上导出的赫姆霍兹自由能与吉布斯自由能，使我们能用其定量判断过程的自发方向及限度[3]。

2 熵的发展——微观物理含义

19世纪，在克劳修斯提出熵(热力学熵或克劳修斯熵)后，科学家们为此进行了大量研究。1872年奥地利科学家玻尔兹曼(L.E.Boltzmann)提出了熵的统计解释，即：

S=klnω

(2)

3 化学熵

大学一年级普通化学或无机化学中也已引进了化学热力学基础知识, 使化学反应中能量的转换得到定量的计算, 因而我们对化学反应的方向不仅可定性判断, 而且从定量上能判断反应方向与进行的限度, 从而使普通化学的内容得到提高与深化。但化学热力学为一门严谨学科, 有着非常严密的逻辑推理与数学推导。其中，关于“熵”这个物理概念，在化学课程中可以通过下面几个实例进行分析和理解，从而也促进我们对物理概念“熵”的认识。

从化学的角度可知，从无序度来说，同一物质气态的熵大于液态的熵, 液态的熵大于固态的熵(如表1所示)。且我们可观察到一个值得注意的规律，即从固态转化为液态(即熔化过程), 熵增量一般只有几个熵单位, 而由固、液态转化为气态(即升华或气化过程) 的熵增量则是几十个熵单位[4]。如何来理解这样一个现象呢？ 从原子排列来说，在固态中分子间距离很近, 堆积较密, 固态是以分子、原子作有序的规则排列为其结构特征的。

表1 一些物质在不同状态下的标准熵J/(mol·K)[5]

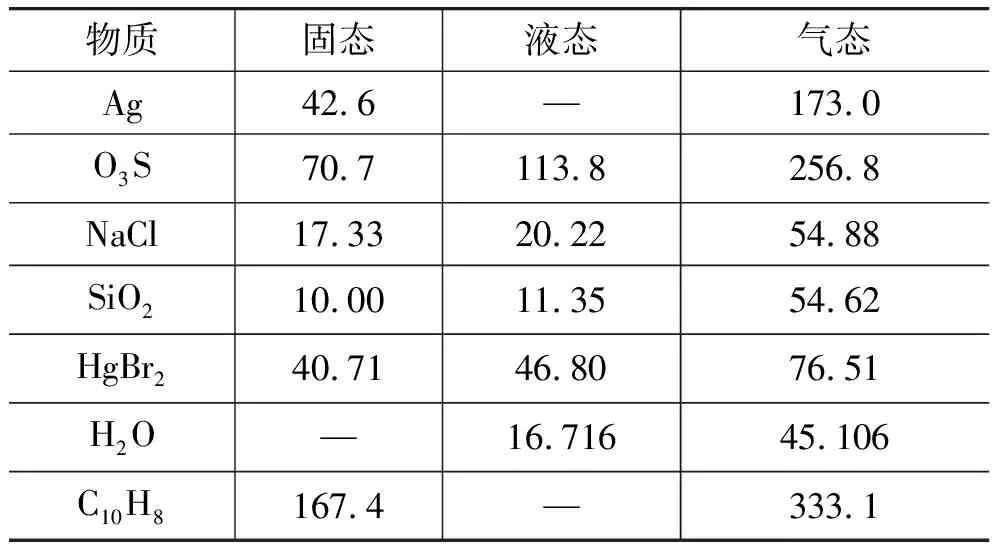
物质固态液态气态Ag42.6—173.0O3S70.7113.8256.8NaCl17.3320.2254.88SiO210.0011.3554.62HgBr240.7146.8076.51H2O—16.71645.106C10H8167.4—333.1

表2 气态乙烯各运动形态相应的标准熵值J/(mol·K)[4]

振动熵转动熵平动熵2.7165.89150.16

从以上数据可看出, 对于处在高度无序状态下的气相来说, 平动熵在3种不同运动形式中占有主要地位。这也解释了为什么当物质由固、液态转化为气态时, 会存在一个比较突出的熵增效应。同时从物理的角度来看，物质分子在气态时比液态、固态下的无序度更大，也验证了热力学第二定律的统计学解释。

此外，从相关数据表[5]中查表可知，一般情况下，分子越大越复杂, 其对应的熵值也越大。如气态卤代烷烃和烷烃化合物的标准熵值如表3所示。

表3 部分气态卤代烷烃和烷烃化合物的标准熵值 J/(mol·K)[5]

这可以从如下进行理解，即分子越大越复杂, 分子所能进行的运动形态就越丰富, 因而对应的熵值也随之增加[4]。再比如同分异构体中, 一般情况下以对称性高的异构体其对应的熵值最低。以气态的烷烃C5H12为例：

图1 C5H12 烷烃的异构体(仅显示碳原子)[4]

由图1可看出,3个分子结构中对称性最高的2,2-二甲基丙烷分子, 其在保持碳原子价键四面体结构的条件下, 碳原子骨架的构型已没有太大变化的余地。这种对称性较高的分子, 原子在空间分布的规律性强, 因而其熵值也较低。在另外两个分子中，即2-甲基丁烷和正戊烷中，由于其对称性不高，分子的空间自由度大，C—C 键易发生“旋转”, 特别是带有*号的碳原子相对于其余碳原子的空间位置变化空间要大很多, 因而该碳原子的骨架可实现多种构型, 从而具有较高的熵值[4]。

从上面的化学常见实例可以看出，若把熵与体系微观状态数或无序度相联系，或是将这个定性的概念与熵的具体数据以及微观图像结合起来, 会发现熵不再是一个玄而又玄、不可捉摸的东西, 而是一个比较生动活泼和形象化的物理概念。

普通化学中“相似相溶原理”的经验规律实质上也是熵效应在起主要作用。所谓相似， 其本质是化学成分、分子量以及结构相近, 作用力相仿。对于相似的组分来说, 往往焓效应不那么突出, 因而混合后熵增这个因素在过程中就会起决定性的作用。在固相中, 对“相似”的条件要比在液相中更为严格。如H2O与KCl能在液相中互溶, 但在固相中是完全不互溶的。在合金或盐类体系中, 组分的原子(离子) 半径和电负性是否相近对能否生成固溶体是有决定性作用的。比如，Cu和Au 由于原子半径和电负性极为相近，因此能生成完全互溶的固溶体系列。而，NaNO3-TlNO3体系由于钾与铊的半径和电负性有相当差别因而生成部分互溶的固溶体序列[4]。

4 熵≠无序

自然界混乱程度倾向于增加的观念被许多人接受，但也容易引起一些错误的认识，最主要的是必须明白ΔS≥0只能用于“孤立”系统。值得注意的是地球并不是一个孤立系统，因为地球不断地从太阳以太阳光的形式接收能量。但也有人认为宇宙是一个孤立系统，即宇宙的混乱程度在不断地增加，从而推测出宇宙最终将达到“热寂”状态。但“宇宙是一个孤立系统”这种说法，严格来说还只是个未被验证的假设。对于一个孤立的体系，体系的熵恒增加。熵增加意味着系统可能的状态数的增加。因此直观上熵增加就与系统的无序联系了起来。但是，所谓的状态数是相空间里的概念，并不必然地同坐标空间里的、视觉上的从有序到无序的变化相一致。熵增加在坐标空间中也可能表现有序来，比如一定条件下小水珠会聚集成大水珠。特别需要注意的是系统某个自由度上的熵的减小可能换来系统总熵的增加。但那个自由度上熵的减小却对应着有序，因而视觉上较明显且容易让人误以为整个体系变得有序了[6]。

5 熵的泛化和应用——麦克斯韦小妖(Maxwell’s demon)

玻尔兹曼的熵公式是物理学史上最伟大的构造之一，是连接经验热力学同其理性基础统计力学之间的桥梁。这个公式不仅仅属于热力学和统计力学，它的对外延伸同样给出了令人震撼的结果。其中最经典的要数麦克斯韦小妖。1871年麦克斯韦在他的《热的理论》一书中设计了一个假想的实验，它几乎动摇了热力学第二定律的基础。该假想的实验假设一个容器内充满温度均匀的气体，这个容器由闸门隔成左右两部分。由于左右两部分的温度是相同的， 根据热力学第二定律，不能利用这两部分来驱动一台热机。但温度相同并不意味着全部气体分子都具有相同的动能，在容器中有的分子运动得快些，有的分子运动会慢些。麦克斯韦让他创造的“小妖”来把守闸门。小妖见到右边飞来的低速气体分子，就打开闸门让它飞到左边去；见到左边飞来的高速气体分子就打开闸门让它飞到右边去。设想闸门的打开和关闭是完全没有摩擦的，于是这小妖无需做功，就可使容器右边温度越来越高，左边温度越来越低。这样一来，系统的熵就减少了[2]。

图2 麦克斯韦小妖

该假想的实验导致热力学第二定律受到了严重的挑战，该小妖也因此被开尔文称为麦克斯韦小妖(Maxwell’s demon)。直到20世纪，人们才弄清楚麦克斯韦小妖并不能推翻热力学第二定律。究其原因就在于，麦克斯韦小妖要想识别分子运动速度的快慢，就需要消耗能量。而从信息论的角度来说，小妖为此花费的能量将多于它完成这种转移后系统增加的能量。因此从总体的角度来说，要想完成这一过程，外界就必须消耗能量，整个体系的熵值最终还是增加的，因而热力学第二定律依然未能被打破。布里渊还进一步分析了信息论中的熵与热力学中的熵的定量关系，得出了公式1bit=kln2(J/K)，其物理意义是：要获取1bit的信息，其熵必定减少kln2=0.957×10-23(J/K)，其中k=1.38×10-23(J/K)。例如T为300K时，就要消耗2.87×10-21(J)的能量。信息的获取必须借助于一定的物质过程，而且伴随着一定能量的消耗，不耗损能量而获得信息是不可能的，所以说孤立系统中的妖魔是不可能存在的。随着各学科的相互渗透和科学综合化发展，熵概念目前已经远远超出物理学的范畴。熵的概念已从平衡态到非平衡态, 从热力学扩展到自然科学其他领域,进而渗透到社会科学的一些领域, 目前已出现各种熵概念，包括统计熵、信息熵、物理场熵、基因熵、气象熵、社会熵、经济熵等，熵与生命、信息、经济和社会等都建立了紧密的联系，说明熵理论具有普遍的适用性和广阔的应用前景[7]。

6 结语

大学物理和化学作为大学理工科学生的基础课程, 在过去的教学中对平衡态熵理论作了较系统的介绍，而关于熵、熵理论及其应用的知识内容介绍却较少。根据当代熵理论的发展, 在教学内容上我们应对非平衡态熵理论的重要概念适当予以补充, 并能通过各种方式(课堂讲授或课外阅读等) 对其他熵理论包括信息熵、物理场熵等作些初步介绍, 使学生对熵理论的发展及其应用前景有所了解。此外，在教学过程中我们应尽量避免“填鸭式”的教学方法，而应采用“互动式”教学，即让学生成为学习的主体，让学生由被动变为主动。比如，在讲熵的泛化及熵应用时，我们可以从如下话题引起：熵可以决定人的生老病死，熵决定某项计划是否可行，熵甚至可以度量社会是否为科学、和谐发展以及宇宙的去向[8]。通过这些新颖的话题，提高学生对“熵”这个抽象概念的兴趣，特别是让学生能根据自己所学知识将熵的概念进一步拓展和深化。这样，不仅可以扩大学生的知识面, 也有利于把学生引向新科技领域的前沿，以适应未来社会的发展，特别是有利于专业人才知识、能力和素质的培养。