在黄昆先生指导下研究固体中的晶格振动、光色散及电声子耦合
——纪念黄昆先生诞辰100周年
2019-10-23贾惟义葛惟昆
贾惟义 葛惟昆
(1乔治亚大学,美国 乔治亚州 雅典市 30602; 2北京大学物理学院,北京 100084; 3香港科技大学,香港 999077)
作为波恩和黄昆经典名著《Dynamic theory of crystal lattice (晶格动力学理论[1])》(国际上习惯地称为 Born & Huang)中文版的译者,我们有机会聆听黄昆先生的教诲,毕生受益无穷。
黄昆先生是举世闻名的伟大的中国物理学家。20世纪90年代, 本文作者之一(贾惟义)和他所在的物理系的理论物理教授茹宾·闵德兹谈起中国大学的教育情况。茹宾对中国物理学家颇感兴趣, 也有所了解。贾问他:“就你所知, 中国哪一位物理学家在世界上颇有影响。”他几乎不假思索地立即回答:“那当然是Kun Huang(黄昆)了。他和玻恩所著的《晶格动力学理论》是最经典的物理学教科书, 那是我大学和研究生时重要参考书。直到现在, 我仍要查阅那里的物理方程。”美国麻州大学物理系主任说,他把Born&Huang像圣经一样摆在自己的书桌上。
《晶格动力学理论》成书于20世纪50年代初[1]。书中涉及了晶体中的声学声子和光学声子在各种情况下的物理方程, 并基于这些结果, 讨论了固体比热、热传导、 弹性、 相变、 压电性、 介电张量、 电致伸缩、 光散射、 光极化及色散、非简谐势对光色散的影响等, 都是那个时代比较热门的固体物理研究课题。相关的理论描述, 对固体物理的研究发展起到了重大的作用。下面用几个例子来说明黄昆先生的理论对我们实际研究工作的指导作用。
1 电声子耦合及同位素效应
从20世纪50年代起, 黄昆先生一直关注由晶格弛豫造成的电声子耦合方面的工作。在辐射跃迁方面,发展了发光光谱中由晶格弛豫造成的多声子跃迁谱[2-6]。简而言之,黄昆理论的精髓就是在光学跃迁的矩阵元中概括了电子和晶格的波函数,即
最后得到包括零声子线的各条声子伴线的强度比值由黄昆因子S表示为
nthpeak∝Sn/n!
这种多声子谱,包括晶体中的色心发光, 半导体及其微结构中的激子激发、发光材料和激光材料中发光中心与晶格声子的相互作用。在这些材料中, 特别是在低温下, 通常能观测到来自纯电子跃迁的锐锋和伴随着这些锐锋的单声子或多声子边带。在一些发光材料中, 由于更强的电声子耦合作用,这些电子跃迁的多声子边带, 提供了宽带发射谱, 这对发光材料的颜色质量的改进起着极为重要的作用。对于激光材料, 特别是3d 过渡离子掺杂的材料, 这些声子辅助的宽带发射, 为可调谐激光器提供了物理上的条件。黄昆先生在研究电子-声子相互作用的理论工作中, 引入了电声子耦合常数S, 被物理学界称之为Huang-Rhys因子(以下简称黄昆因子), 用来衡量电子-声子相互作用的强度[2-6]。 有鉴于此, 我们或许可以把电子-声子耦合态称之为 Huang-Rhys态, 把依电声子发射谱做成的激光器统称为Huang-Rhys激光器。
作为本文的第一个例子,我们介绍电声子耦合作用中的同位素效应, 所涉及的晶体是准一维反铁磁晶体[7,8]:
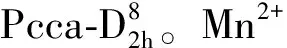

图1 两种晶格样品在1.6K温度下4T1→6A1的发射谱(a) CsMnCl3·2H2O(CMC-H)和CsMnCl3·2D2O(CMC-D); (b)中激子及其磁子边带与声子边带(p偏振, T=1.6K)
图1给出两种晶格样品在1.6K温度下4T1→6A1的发射谱[8,9]。发射谱由3部分组成:弱的锐锋(586.0nm、586.7nm), 是纯电子跃迁峰;较强较宽的磁振子支助的电子发射峰(586.8nm、587.4nm), 由于磁振子在布里渊区态密度分布, 该峰形状远离洛伦兹分布;最后又强又宽的发射带就是所谓的多声子支助的跃迁, 常称为声子边带。在这里, 电子的光能主要来自 Huang-Rhys耦合态, 从图1可以看到:
(1) 同位素替代可引起发射谱线位移。由H到D,零声子线红移了18cm-1。声子边带红移了65cm-1。这种红移来源于晶格的缩小和晶场的升高, 导致4T1能级下落。同位素替代引起的光谱位移早就被观测到。如在MgO:Cr3+, Cr3+同位素每增加1, Cr3+发射线蓝移0.13cm-1[10]。
(2) 同位素替代D→H 使零声子线强度增加了近9倍。
(3) 除去发光强度外, 含结晶水和结晶重水样品的发光谱线的强度分布形状几近相同。根据黄昆理论[6], 拟合出来的黄昆因子也几乎相同:
SH=9.5,SD=9.7.
(4) 对两种样品发射寿命的测量表明, 同位素替代对发光寿命产生了极大的影响, 含水H2O样品的0.58ms, 增加到含结晶重水样品的9.2ms, 增长了近15倍。
(5) 通过同位素替代实验, 我们可以推断, 含H和含D的多声子发射边带, 捲入的仅仅是与Mn2+八面体直接相连的配位离子相关的晶格振动模。在强耦合近似下, 相关的多声子边带具有近似高斯分布形式。按黄昆先生的理论, 可以求得多声子发射谱中的平均声子能量[6]:
这与该两种样品中低频拉曼散射模的结果一致[11]。参与多声子辐射跃迁的声子模的频率, 受同位素替代的影响忽略不计。
(6) 另一方面, 卷入无辐射跃迁过程的声子, 应该是H2O和D2O相关的高频声子, 即H2O和D2O的伸展振动模
按照量子力学理论, 多声子无辐射跃迁几率, 依赖于跨越从激发态到基态能隙(CMC-H,17065cm-1; CMC-D 17047cm-1)的声子个数(声子阶数)。声子数越小, (阶数越低,) 无辐射跃迁几率越大;相反, 声子数越大, (阶数越高,) 无辐射跃迁几率越小。对于CMC-H, 需要5阶声子, 对于CMC-D, 需要7阶声子, 因此, 在 CMC-D 中, 无辐射跃迁几率要比CMC-H小很多。在紫外灯照射下, 人眼看不见紫外光, 只能看见由样品发出的可见光, CMC-D的发射光要比 CMC-H亮几倍。
假定CMC-H和CMC-D中多声子无辐射中电声子耦合常数S相近。根据黄昆先生的理论[6], 利用实验参数, 如τD=9.2ms,τH= 0.58ms, 能隙~17065cm-1, 17047cm-1, CMC-H=3360cm-1, CMC-D=2700cm-1,可以得到电子-高频声子耦合的黄昆因子S=2.3。这是一个合理的估算值。
另外, 请注意, 在图1(a)的731nm处和图1(b)的697nm处都没出现相应2700cm1和3360cm1的声子峰, 再次表明, 高频声子不卷入辐射跃迁。
(7) 本实验涉及的是准一维单晶, 激活离子Mn2+沿Cl-Mn-Cl-Mn-Cl键分布(a轴), 键间距较大。因此处于Mn2+激发态的电子将沿a轴传送自己的激发能量, 因此陷入陷阱的几率大大降低, 这使Mn2+的“浓”系统的发光一直延续至室温。而在三维晶体结构中, 如MnF2, 在30K以上, 其发光就淬灭了。在掺有高淬灭离子 Fe2+, Co2+, Ni2+的CMC晶体中, 在室温下仍可观测到Mn2+离子的发光[12]。因此, 具有低维度结构的系统, 似乎具有较高的发光效率。这一点也可以在人造的低维半导体结构中观测到。如二维电子气、量子阱、量子线、量子点等,发光效率一般高于块状样品。
(8) 这里介绍的准一维反铁磁晶体材料, 并不具备实际应用价值, 但它确是物理上研究电声子耦合的理想对象。当前红外有机发光材料, 有机LED等颇受重视。在这些有机材料中多含有H基集团, 如CHn, OHn, NHn,它们都含有高频声子团。如果通过氘化过程, 将H置换成氘,有可能使得这些材料的发光效率提高。
2 束缚激子的声子伴线的黄昆因子辨析
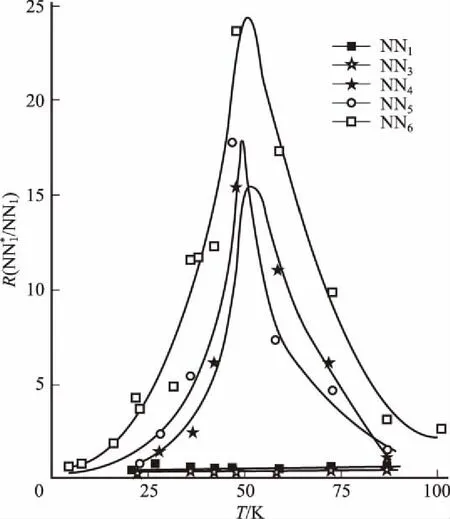
图2 法国研究组得出的表观黄昆因子与温度的依赖关系
在1972 年第一届全国半导体物理会议上,黄昆先生做了一个关于“局部声子与束缚激子”的邀请报告。在“文革中”科学界万马齐喑、极度闭塞的条件下,黄昆先生仍能敏锐地抓住当时半导体物理发展的前沿课题。本文笔者之一(葛惟昆)在现场聆听了黄先生的精彩报告,并在此后的工作中沿着这两个方向做了一些有益的尝试。他在1984年从英国读完博士学位后回到中科院半导体所,直接在黄昆先生指导下工作。恰好那时法国一个著名的研究组在GaP中等电子中心N和NNi对(i表示两个N原子的间距,i值越高,间距越大)发光的声子伴线研究中,得出了极为反常的黄昆因子。N 和 NN 对在GaP中由于是等电子中心、深能级,成为非常有效的绿光发光中心。根据法国研究组的报导,NN4, NN5,和NN6的光学声子伴线的黄昆因子S随温度剧烈变化,从低温的0.2左右,升高到50~60K时的20左右,再到高温时回降到0.2左右(见图2)。其低温光谱如图3所示。而按照黄昆理论,S不应当是一个温度敏感的参数。法国研究组不但做出了奇怪的实验结果,还试图在理论上推翻黄昆理论。黄昆先生对自己的理论充满自信,他表示如果对方的理论发表,他会予以评论。这样对方没有发表理论,但坚持自己的实验结果。
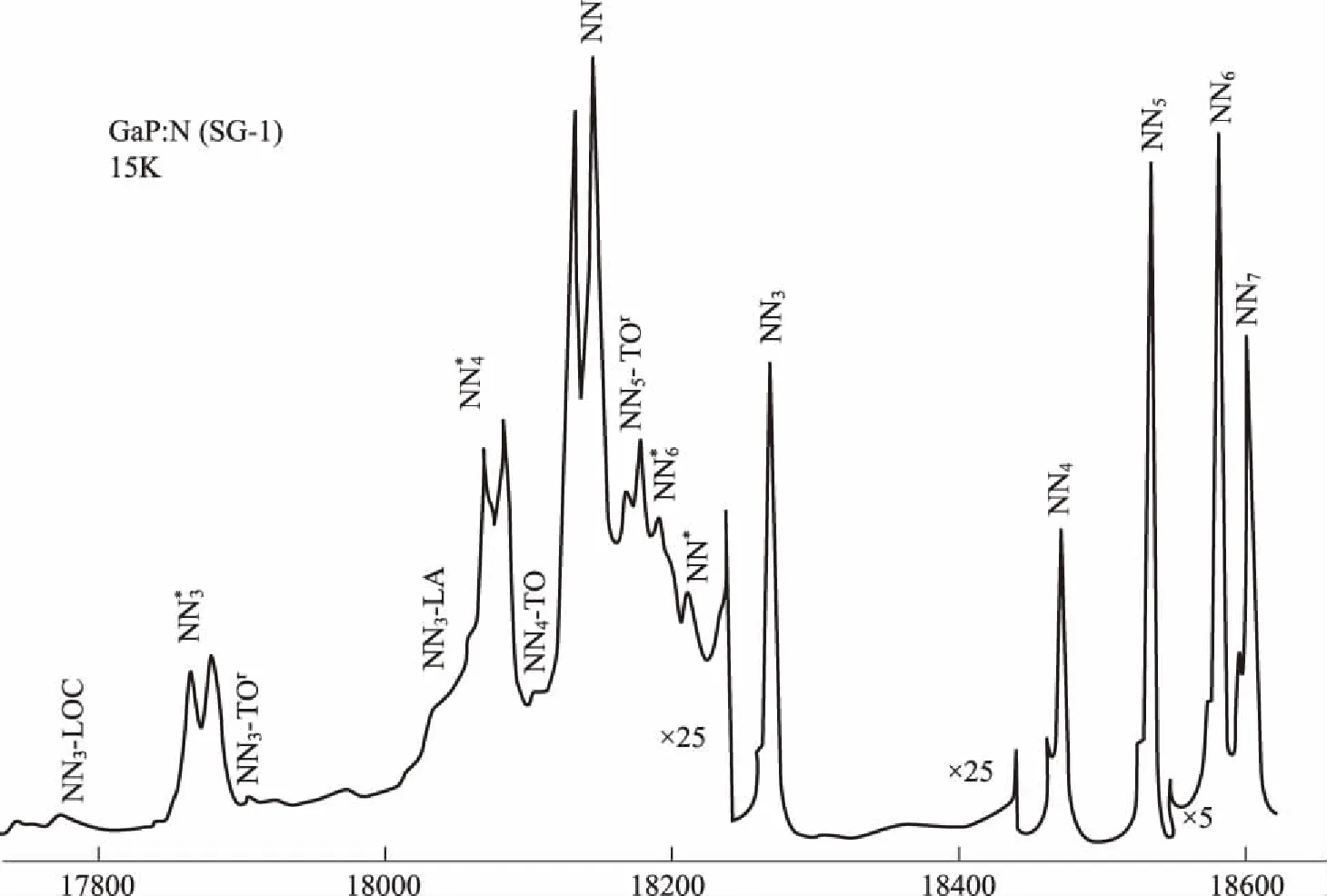
图3 GaP:N 光谱图 (15K)
在黄昆先生的指导下,我们以判断性的实验结果证明[13],法国研究组在实验中犯了一个光谱研究中最致命的错误,就是把谱线识别错了。原来随着温度变化,NN对之间的载流子会互相转移。当温度升至50~60K时, NN3谱线相对于NN4,5,6的谱线相对地增强很多。而NN3的声学声子伴线,恰恰与NN4,5,6的光学声子伴线相重合, 因此如果把NN3的声学声子伴线当成NN4,5,6的光学声子伴线,就会误以为后者的光学声子伴线的黄昆因子得到了反常的提高。为了毫无争议地说明这一点,我们在光致发光(PL)实验中用可调谐激光器对样品做选择激发。当激发光的光子能量落在NN3与NN4,5,6的零声子线之间时,后者(NN4,5,6)及其声子伴线不可能出现,但在本该是它们的光学声子伴线的位置,仍然有很强的发光,那正是NN3的声学声子伴线。也就是说,法国研究组错把NN3的声学声子认成NN4,5,6的光学声子,于是得出荒谬的实验结果。在此基础上,我们认真钻研了黄昆理论,研究了产生声子伴线的形变势和极化势,从理论上也获得了S的实际量值的确大约为0.2,并且基本不随温度变化,与实验结果完美相符[14]。这件工作得到黄先生的充分肯定。
3 半导体中局域模声子的红外与拉曼光谱研究
在黄昆先生1972年的同一个报告中,介绍了当时刚刚起步的局域声子的研究,预言它在半导体杂质缺陷研究中会具有重大意义。所谓局域声子,是杂质后缺陷引起的有别于晶体简正模式的晶格振动模式。由于杂质或缺陷与原来晶格中的原子质量不同以及与近邻原子的作用力不同所产生的晶格振动频率可能落在简正模式声子的能带之外。特别当一个比较轻的元素作为杂质时,其振动频率会超出光学声子能带的上限,被称为局域振动、或局域模(Local vibration mode, LVM),因为这种振动不会在整个晶体中传播,而是局域在杂质附近,如图4所示。局域模震动频率可以表达如下:
其中Mimp和kimp分别是杂质的质量和它与最近邻原子间的力常数;c是一个由键角和键合力决定的参数;Mnn是最近邻原子的质量。

图4 局域模的示意图
(1) 我们在局域模声子方面做了两件比较有意义的工作,一件是20世纪80年代末关于GaAs 中O 的局域振动的发现和研究[15,16],由于它与GaAs中最重要的深能级EL2密切相关,所以当时引起国际半导体物理界的重视,在国际半导体会议上曾列为专门的分会主题。相关的红外吸收谱比较复杂,在710cm-1到730cm-1之间分为3组(A,B,C, 见图5),位置在每一组又分为三个小峰(见图6),其相关的O原子占位模型见图7。O把砷原子替换了, 但并未占据砷原先的位置,而是在最近邻的4个Ga原子中, 断掉与其中两个的键合,只与另外两个结合在一起。所以观测到的局域模振动与这两个Ga原子紧密相关。由于Ga原子有质量为71和69 的两种同位素, 所以两个Ga原子有3种组合的方式,使得观察到的LVM谱峰分类为3个尖锐的小峰,分别对应于Ga69-Ga69, Ga69-Ga71, 和Ga71-Ga71。而这3个小峰的强度之比与Ga的两种同位素的丰度比完全吻合。

图5 O在GaAs中的LVM红外吸收峰
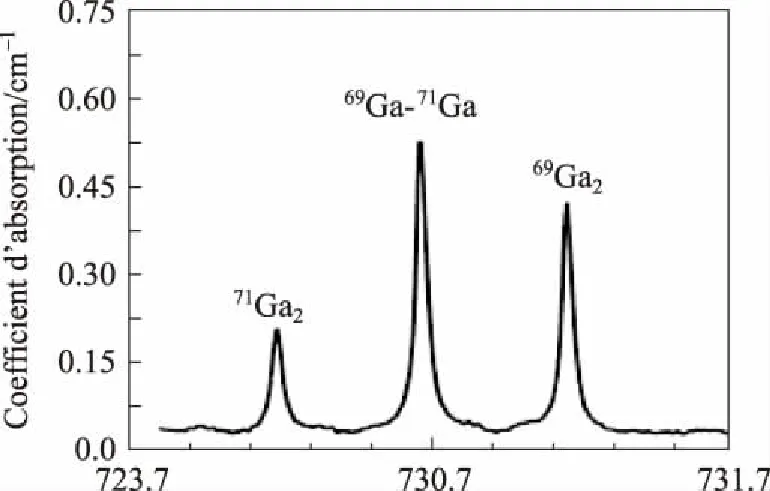
图6 Ga同位素导致的谱线分裂

图7 O杂质在GaAs晶格中的占位
最有趣的是,当我们用1.25 eV 的激光长时间照射样品以后, A, B, C 3组的强度发生了奇妙的变化,如图8中的实验点所示。这是由于A, B和C 3组吸收峰分别相应于O+, O0, 和O-3个能级。而由于激光对EL2能级的激发和EL2 能级反过来俘获导带电子,造成准费米在O的能级附近上下移动,它在3种电荷态的占据随光照时间而反复变化。我们据此做了模拟计算, 得出图8 中实线的结果,与实验基本符合。

图8 A,B,C 3个峰随光照时间的强度变化横坐标为光照时间(分钟)曲线为模拟结果
(2) 最近的一件局域模方面的工作,是关于GaN中的C,2018年发表在Phys.Rev.Let上[17]。C在GaN中是形成半绝缘态的关键杂质。但是C在GaN中占据的晶格位置长期处于争执之中。我们用红外反射谱和拉曼光谱, 毫无质疑地确认了C主要是占据N位。我们的结果示于图9(a)、(b)中,同时第一性原理计算也得到与实验完美一致的结果, 参见表1。 对于CN的对称性也做了研究,证明在红外反射谱和拉曼光谱中所观察到的毫无疑问是占据N位的电荷为负1的C杂质。

图9 GaN中CN LVM的红外反射(a)与拉曼散射(b)谱

C related defectCalculationExperimentC-NFrequency/assignmentRatio(Nonpol.)Ration(z(xx)z)Ration(z(xy)z)773(ν1)/A1766(ω1)/A1778(ν2)/E,774(ω2)/E781(ν3)/E2.3∶1.02.2∶1.04.4∶1.04.3∶1.0~0~0C0NFrequency726,728,759C+NFrequency703,715,720CN-O0NFrequency757,777,803C+GaFrequency837,840
4 基于Huang-Rhys电声子耦合态的可调谐激光器

图10 简化的d2离子在Td 晶体场中的TS能级
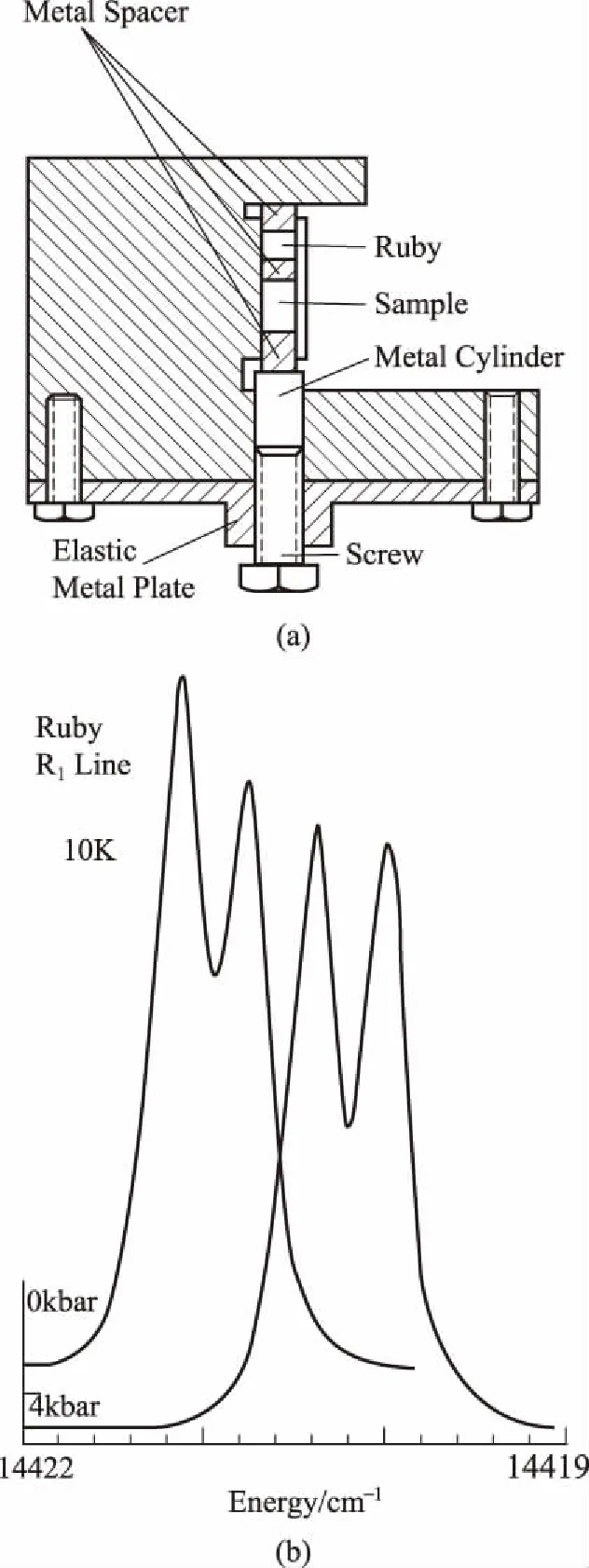
图11 (a) 压力装置; (b) 校正压力的红宝石压力谱
最后, 应该指出的是, 在最近三、四十年里, 利用Huang-Rhys的电声子耦合态, 发展出各种可调谐激光器, 这包括LiF色心激光器、Cr3+离子金绿宝石激光器、Ti3+宝石可调谐激光器, 及掺Cr3+的氟化锂锶铝激光器。Cr4+掺杂的多种晶体曾用于制造近红外可调谐激光器。在研究这类激光器时,首先遇到的问题是它的纯电子跃迁峰的来源问题。图10给出Cr4+(3d2)的简化了的立方晶场Tanabe Sogano(TS)能级图[18]。图中的3T1,3T2和3A1能级是自由离子Cr4+(3d2)基态3F在立方晶场劈裂能级,而1E则是由1D能级分裂出来的。这一能级分布图类似于红宝石激光器(Cr3+:Al2O3)中Cr3+能级图(4T1,4T2,4A2和2E)。红宝石激光来自2E能级的发射[19]。在Cr4+激光中,发光是来自1E能级,还是3T2能级? 这曾引起研究者们的困惑和歧见。澄清这一问题的最佳途径是在应力下测量发射谱的变化。由图10可见,E能级大致与晶场强度轴平行,而T能级随晶场很快地升高。对红宝石而言,发射谱随压力的变化大约0.182cm-1/kbar。如果发射谱来自T能级,那么发射谱线随压力变化要快很多。为此我们设计了一个小巧的压力装置(图11)[20]。这个装置可方便地加到光学用低温制冷机的冷指上。通过一个光学窗口,用改锥转动加压螺柱,可以调节加压应力。应力器中也加有红宝石样品,用来标定所加应力的大小。

图12 镁橄榄石单轴应力(沿a 轴)下的光谱零声子线随压力兰移

图13 掺Cr镁橄榄石的单轴应力(ab面上,偏离a 轴)近红外荧光的赝分裂
作为一个例子,图12和图13给出Cr4+:Mg2SiO4(镁橄榄石)单晶的发射谱(零声子线部分)随应力的变化[21]。 零压力下零声子线处于1094.5nm(9137cm-1), 1092.8nm(9151cm-1), 和1090.6nm(9169 cm-1)。当压力沿晶体a轴方向时, 零声子线几乎是同步地移向短波长, 移动速度10cm-1/kbar, 是红宝石移速的50多倍。当压力沿b轴时, 谱线随压力红移; 压力沿c轴时, 谱移很小(未给出数据图)。三峰同步移动,说明这3个发射峰来自3T2, 对应于自旋三重态的自旋-轨道分裂。这一分裂对晶场变化(应力所致)不敏感。图13所示是应力在ab平面, 且偏离a轴15°时发光谱线的赝分裂。Mg2SiO4具有正交对称性, Cr4+替代硅四面体SiO4中的Si。每个单胞含有4个化学分子, 因而有4个硅四面体, 它们是等价的。当施加的应力偏离晶轴方向时,这4个四面体就只能两两等价了, 在那里代入的Cr4+离子也只能两两等价。而对于应力下不等价离子对的发射谱线就不同了, 如图13所示。这种谱线分裂来自应力感生的非等价晶座, 而不是同一晶座上的Cr4+离子能级3T2的轨道三重态。因此,图13所示的谱分裂称之为赝分裂。
类似的应力实验也用于Cr4+:Y2SiO5和Cr4+:Y3Al5O12, 获得了类似的结果。我们曾用Cr4+:Y3Al5O12单晶构建了一台Q-开关激光器(图14)和连续调谐激光器(图15)[22]。和发射谱相比, 激光的调谐曲线都向长波移动了。在室温下, 发射谱和吸收谱有所重叠, 激光的起始阈值由于激发态吸收而增高。这是Huang-Rhys激光器普遍存在的问题, 但对应用没有什么大影响。
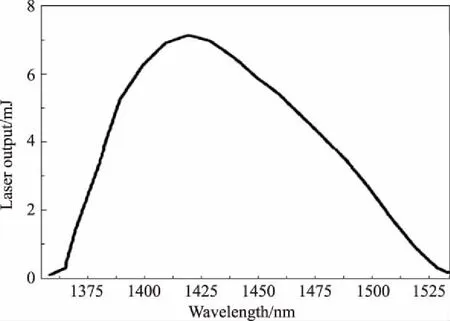
图14 Q开关泵浦的调谐曲线

图15 Cr:YAG cw 激光器的调谐曲线
此外, 前面曾提到, 红宝石激光器(694.3nm)中Cr3+受激发射的亚稳态是2E能级, 它处于4T2能级之下(参考图10), 称之为高晶场情况。2E能级与晶场强度轴几乎平行, 意味着其上的电子与晶场或者说与声子相互作用很弱, 不会出现电声子发射带。在Cr4+掺杂的晶体中, 亚稳态是3T2能级, 它处于1E能级之下(图10), 称之为低场情况。3T2能级随晶场很快升高, 这意味着其上的电子与声子有很强的耦合作用, 会出现强而宽的电声子发光带。这样的晶体适用于可调谐激光器。Cr3+也可以处于低晶场环境, 如在金绿宝石中: Cr3+:BeAl2O4。
5 结语
当我们回顾这些以往的工作时,深深感到能在黄昆理论和黄昆先生本人的指导下开展科研工作,实在是我们学术生涯中最大的幸事。黄昆先生的学问、治学和为人,都是我们终生的榜样。 当《晶格动力学理论》一书重印的时候,译者之一(葛惟昆)负责了全书的重校,发现中译本存在许多小的笔误之类,而英文原版一点错误也没有。他当时无限感慨地写下了“重印后记”。
“《晶格动力学理论》是黄昆先生建树的一座丰碑,确立了他在固体物理学史上不朽的地位,也是他留给后人最宝贵的财富。面对这样一部辉煌的巨著,译者时时有一种高山仰止、诚惶诚恐的感觉。反复阅读其英文原版,不仅被它的博大精深所折服,也为它的严谨细腻而惊叹。”
就让我们以此来结束本文,借以表达我们对黄昆先生的崇敬和思念!
