最大熵原理在推导分子数分布中的应用

庆秉承 刘 萍 陈晓珂 胡 祎 王致远 胡云婷 韩英卓 田篷勃 方爱平

(西安交通大学理学院，陕西 西安 710049)

在物理学中熵是反映系统无规程度的量度。1948年，Shannon提出信息熵的概念[1]。事实证明，信息熵和热力学熵有一定的统一性。根据熵增加原理，在一定条件下，孤立系统在达到稳态时，其熵值将会趋于某个极大值。因而在1957年，E.T.Jaynes提出最大熵原理[2]，即：一个稳定宏观系统某个物理量的信息熵在约束条件下趋于最大值。由于信息熵的大小和该物理量的概率密度分布函数f(x)有如下关系：

式中，f(x)为该物理量的概率密度分布函数；D为概率密度分布函数的定义域。

根据最大熵原理，只需求得使信息熵在约束条件下达到最大值的函数f(x)，便可确定该物理量的概率密度分布函数。为求得f(x)，可以利用拉格朗日法求泛函的约束极值。

最大熵原理被学者广泛研究，利用最大熵原理，蓝风华推导出了麦克斯韦速率分布[3]；晋宏营推导出了电介质极化规律[4]；方爱平、田蓬勃等人应用最大熵原理，在信息缺失的条件下最大效率地实现对全局进行判断和决策[5]。但鲜有学者用最大熵原理研究分子数密度按自由程以及按高度的分布，本文将利用最大熵原理，研究这些问题。

1 推导分子数密度按自由程分布

在秦允豪先生的热学教材中，为推导分子数按自由程分布，通过小孔泄流模型，得到了结果[6]。本文通过最大熵原理，重新推导分子数按自由程分布。

利用拉格朗日乘数法，得到

结合约束条件，解得

则最终得到分子按自由程分布服从指数分布，与教材上的结果一致，即为

2 推导分子数密度按高度的分布

在秦允豪先生的热学教材中，给出了等温条件下，分子数按高度的分布[6]。而本文将利用最大熵原理，推导考虑温度分布情况的分子数按高度分布。

2.1 理论推导

设分子数按高度分布的概率密度分布函数为f(h)，考虑分子平均能量应为一个定值，即

式中，m为单个分子平均质量；h为位势高度(Geopotential height)；k为玻尔兹曼常数；T为热力学温标。式中近似认为分子能量仅仅包括重力势能和分子动能，且空气分子为刚性双原子分子。

则根据最大熵原理，有

利用拉格朗日乘数法，得到

得到

将其代入归一化条件，得到

最后得到(参数β待定)

2.2 结果验证

(2) 变温情况 此时，为了获得大气温度随高度的变化，参考美国NASA公布的Standard Atmosphere中给出的大气温度随高度变化的数据[7]，数据如图1所示。

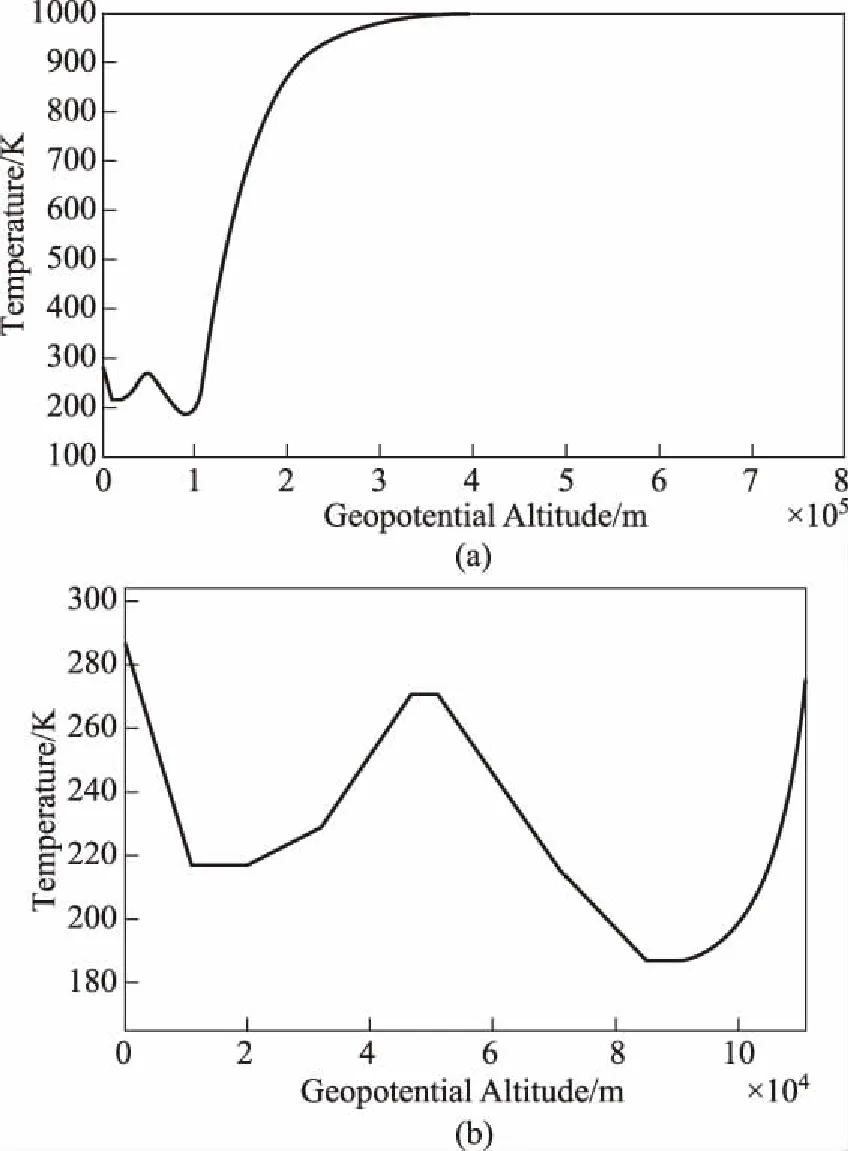
图1 大气温度随高度变化((a) 为全高度; (b) 为近地区细节)

满足归一化条件，又由于拉格朗日乘子的唯一性，故该拉格朗日乘子取值是正确的。

由此可以得到分子数按高度分布的情况，由于

则分子数密度n满足

可见n与f(h)呈正比例关系，将NASA发布的分子数密度随高度变化的曲线[7]与通过上式计算得到的分子数密度随高度分布的曲线进行对比，结果如图2所示。

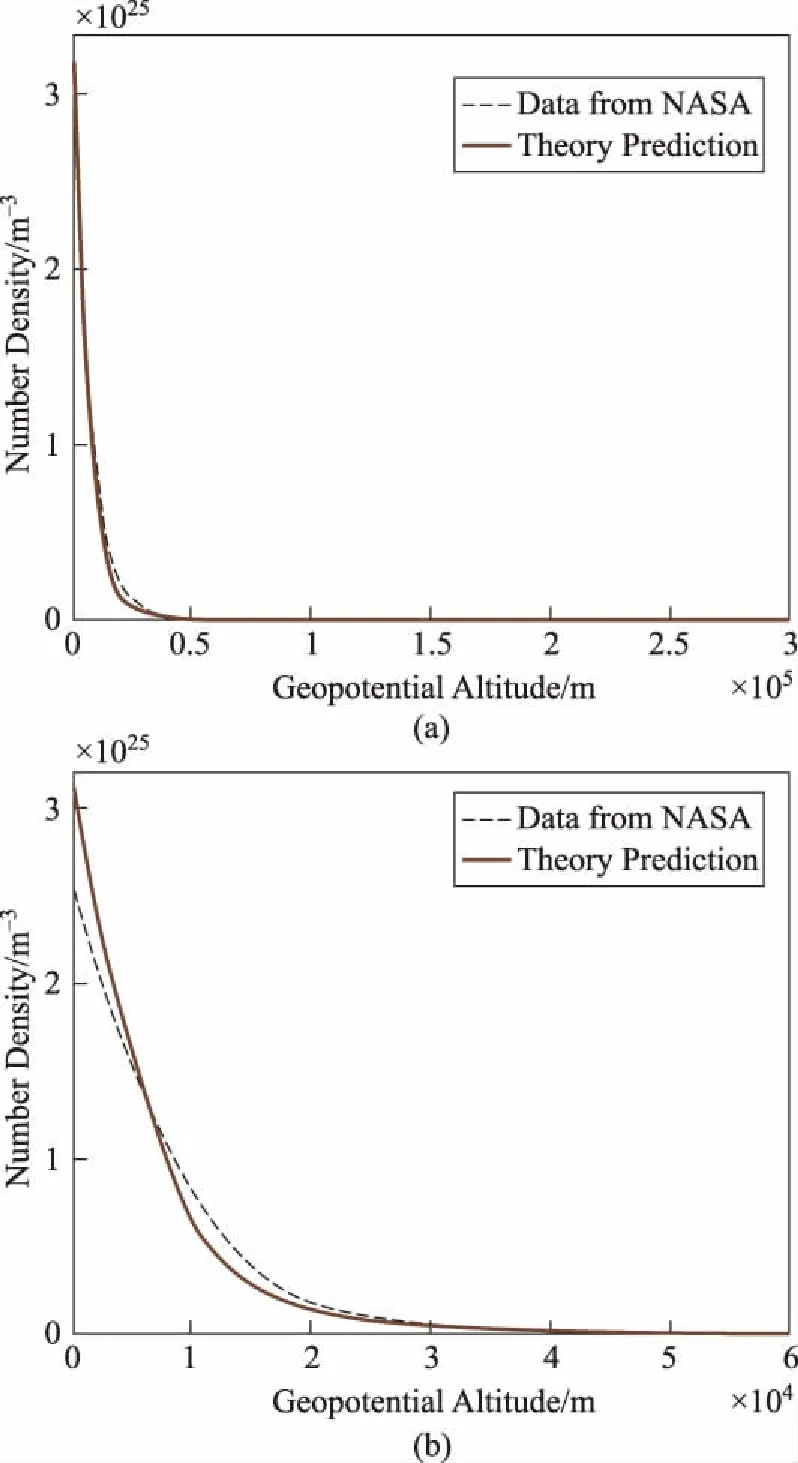
图2 分子数密度随高度变化((a) 为全高度; (b) 为近地区细节)

可见二者吻合较好，说明上文通过最大熵原理进行的推导是合理的。

3 结语

本文首次通过最大熵原理研究分子数按自由程的分布，基于更弱的假设，得到的分布函数和教材吻合，有更好的普适性。首次利用最大熵原理研究了温度变化情况下，分子数按高度的分布，结果和NASA的数据相吻合，该结果将有利于预测更高海拔的分子数分布。上述结果表明最大熵原理在统计物理中的应用是合理的，这或许隐含了统计物理和信息论的内在联系。