单孔不耦合装药爆破的岩体损伤分布特征研究
2019-10-08张继春石洪超邹新宽邓稀肥
潘 强, 张继春, 石洪超, 邹新宽, 邓稀肥, 许 宏
(1.西南交通大学 土木工程学院, 成都 610031; 2.成都工业学院 建筑与环境工程系, 成都 610039;3.自贡市城市建设投资开发集团有限公司, 四川 自贡 643000; 4.中国中铁四局集团有限公司, 合肥 230023)
岩体在形成及演化过程中,其内部存在诸多微裂纹等初始损伤。在动态或静态荷载作用下,岩体中的初始损伤被激活,不断扩展贯通并逐步形成宏观裂隙,最终导致岩体宏观物理力学性能降低甚至破坏,因此,岩体破坏是一个损伤不断累积演化的过程[1]。通常在岩体爆破过程中,爆破动力作用不可避免地对岩体造成不同程度的损伤,由于损伤是一个不可逆过程,当其累积到一定程度将造成岩体物理力学性能弱化甚至破坏,由此危及到岩土工程结构的质量与安全。目前国内外对爆破作用下岩体损伤研究越来越多,所取得的大量研究成果主要集中在岩体损伤本构模型[2-4]、岩体损伤演化机理及其损伤特性[5-8]、岩体损伤安全评价[9-10]以及岩体损伤控制技术[11-13]等方面。其中,岩体损伤范围与损伤程度是损伤特性研究中两个极其重要的参数,对围岩安全性评价以及工程支护优化设计具有重要的作用。迄今,对岩体爆破损伤范围内的损伤分布特征研究还相对较少,在这方面开展研究不仅可以了解损伤分布规律及其与爆破参数的相互关系,预估爆破损伤范围和控制爆破损伤程度,而且对围岩体加固措施优化具有指导意义和参考价值。
针对单孔爆破损伤,戴俊等[14]通过模型实验发现,炮孔周围的损伤因子随距离增大近似呈幂函数衰减,拟合出了损伤因子与比例距离的关系式。唐红梅等[15]根据弹性模量与应力波在岩体内传播频率成正比建立损伤关系式,同时又根据爆破主频率与药量、爆心距的关系,综合确定了爆破损伤分布规律并划分各个分区的大致范围。索永录[16]通过煤样超动态应变测试,提出爆破中区应变峰值体积应变符合幂函数衰减规律,结合Taylor和Grady等爆破损伤模型中损伤参数表达式,建立了煤层预先弱化爆破宏观损伤破坏程度的分布函数。潘鹏飞等[17]通过数值模拟研究得出损伤因子与爆破距离呈现指数函数衰减规律,并拟合出相关参数。尽管上述研究成果在一定程度上丰富了岩体爆破损伤理论,但尚有进一步完善之处:采用模型实验和数值实验拟合出的经验关系式还需要理论支撑;已有的理论分析成果仅考虑了应力波对损伤演化的贡献,未考虑准静态气体的作用;此外,采用应变分析时仅考虑体积应变,未考虑等效应变的影响。因此,有必要从爆炸应力波和准静态气体共同作用角度进行岩体爆破损伤的理论解析,进而为模型实验和数值实验提供理论指导和参考依据。
本文基于岩体爆炸力学与弹性力学,将爆炸应力波和准静态气体共同作用过程作为岩体爆破机理分析的切入点,采用有效弹性模量建立单孔爆破下岩体损伤分布特征的理论关系式,为岩体加固设计和合理确定爆破参数奠定理论基础。
1 损伤定义及其分区
1.1 损伤定义
损伤定义目前没有统一的形式,采用间接的宏观材料参数表征损伤程度(损伤因子),是目前常采用的方法。根据宏观物理力学参数可建立如下岩体损伤因子D的关系式[18]
(1)
式中:E0为爆破前岩体的弹性模量;E为爆破后岩体的等效弹性模量;c0为爆破前岩体的声波速度;c为爆破后岩体的声波速度;Kz为岩体完整性系数;η为岩体声波速度降低率。
严格意义上,D>0即表示岩体受到损伤,但是考虑到爆破损伤对岩体产生的影响,国内《水工建筑物岩石基础开挖工程施工技术规范》(SL47-94)规定[19],当η>10%时,即可判定岩体受到爆破损伤影响,对应的岩体损伤阈值为Dcr=0.19。
1.2 损伤分区
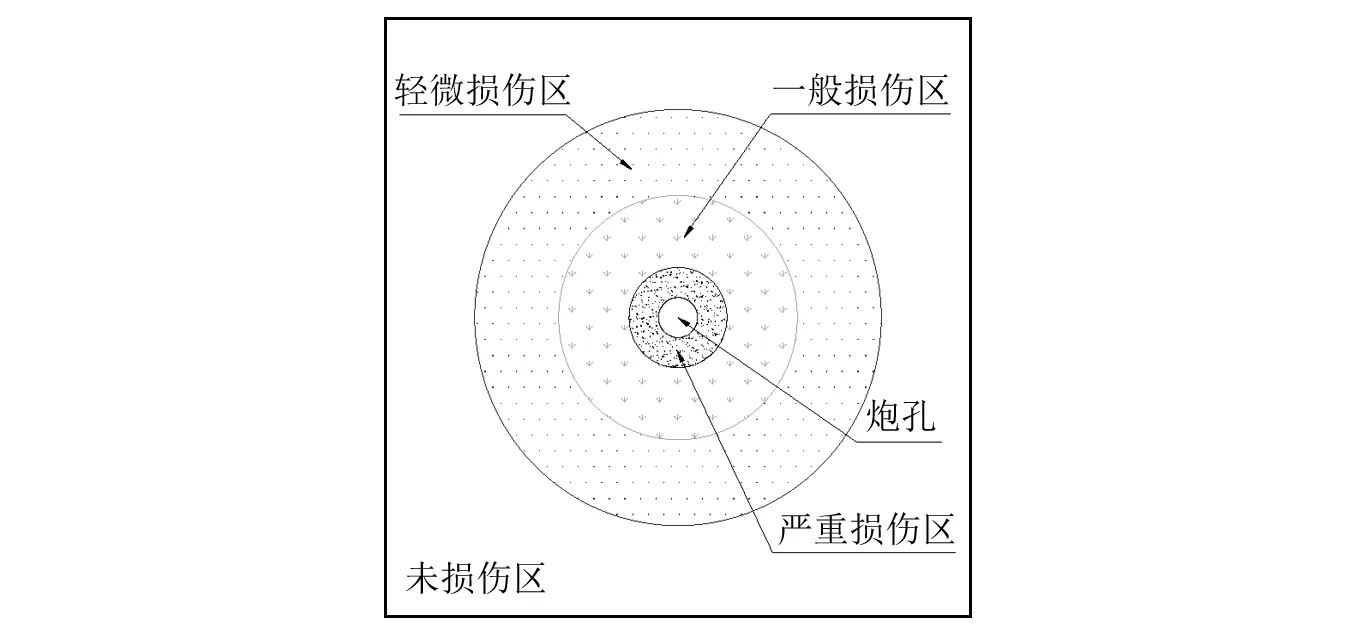
通常,耦合装药或不耦合系数较小的装药在岩体内爆炸会因强烈的冲击作用而形成以炮孔为中心的粉碎(压缩)区、裂隙区和振动区。工程上为了减小爆破对保留岩体的扰动,多采用不耦合装药结构以削弱这种冲击作用,消除粉碎(压缩)区,从损伤角度看,就是避免岩体产生“裂而不碎”的严重损伤区,为此,定义岩体爆破时产生“裂而不碎”的最大不耦合系数K0为临界不耦合系数(其值与岩体性质和炸药性质等有关)。当不耦合系数K≥K0时将不会产生岩块破裂,可将炮孔周围岩体划分成3个区域,以炮孔为中心依次为一般损伤区、轻微损伤区和未损伤区,如图1所示;当K 图1 K≥K0的损伤分区Fig.1 Damage partitions of K≥K0 图2 K 上述各区域内岩体损伤表征为岩体内微裂纹(缺陷)扩展与贯通,是爆炸应力波和准静态气体共同作用的结果,各损伤区域内岩体损伤特征可定义如下:严重损伤区——岩体结构面及岩块均破裂,但并未完全形成相互交叉的块体,即岩体内爆破裂缝未完全贯通;一般损伤区——岩体结构面破裂,岩块未产生破裂,即岩块内的微裂纹并未扩展形成爆破裂缝;轻微损伤区——岩体结构面局部破裂,但破裂缝扩展极其有限,岩块内的微裂纹未扩展;未损伤区——随着距炮孔距离增大,压力逐渐降低,不足以使岩体微裂纹产生扩展,该区域内岩体未受到损伤。 爆破荷载下同时存在两种不同形式的作用,即爆炸应力波的动态作用和高压爆轰气体的准静态作用,两者均对岩体造成不同程度的损伤。而且,两个作用过程时间上有先后区别,但错综复杂,很难将其完全分割开来。虽然光面爆破或预裂爆破采用了不耦合装药结构,极大地削弱了爆炸冲击波作用,但是爆炸应力波对岩体造成的损伤可为爆轰气体作用提供有利条件,因此爆轰气体准静态作用下产生的损伤不容忽视。因此,有必要研究两者共同作用下的损伤分布特征。 对于光面爆破或预裂爆破而言,由于相邻孔间的应力集中现象导致裂纹尖端出现应力奇异性,使得裂纹沿炮孔连线方向定向扩展,其他方向的裂纹扩展受到抑制,炮孔连线上的应力集中区域相对于围岩损伤区域很小,可以忽略其对围岩损伤的影响,因而可简化为单孔爆破以便于进行解析分析。 对于均质材料爆破前的初始参数较易获取,而经过爆破作用后材料参数的变化分布特征规律尚不清楚,而且针对某一质点而言爆破作用之后其波速c将随着时间变化,由于应力波传播速度快于微裂纹的扩展速度,关系式σ=ρcυ中的波速仍是爆破前原始波速c0,因此建立爆破后波速与应力之间的关系式尚且困难。材料损伤的实质是微裂纹的形核、扩展和连接,而细观损伤力学正是对微裂纹等进行力学描述。细观损伤力学一方面忽略了损伤过于复杂的微观物理过程,避免了统计力学浩繁的计算,另一方面又包含了不同材料细观损伤的几何和物理特征,为损伤变量和损伤演化过程提供了较明晰的物理背景。细观损伤力学采用平均化思想,把细观结构损伤机制研究的结果反映到材料的宏观力学行为的描述中[20]。因此,可从细观损伤力学微裂纹体的有效模量角度沟通微裂纹体与损伤分布特征之间的相互关系。 炸药处于炮孔中心,高压爆轰气体以极高的相同速度向四周膨胀并作用于炮孔壁面。另外,岩体通常处于一般初始地应力状态,初始地应力相对于爆破荷载而言很小,同时岩体在爆破荷载作用下表现出准脆性特征。针对光面爆破通常采用的径向和轴向不耦合装药结构,由于装药段的岩体爆破损伤大于空气间隔段[21],因此,从最不利角度出发仅考虑线装药密度一定时装药段范围内不耦合装药爆破的损伤分布特征,为突出重点,简化分析,便于更好地借助力学理论进行解析分析,特作如下假定:①不考虑岩体初始地应力的影响;②炮孔压力呈均匀分布;③岩体为含有均匀随机分布微裂纹的弹性材料;④分别考虑爆炸应力波与准静态气体作用。 根据细观损伤力学理论,有效模量计算方法主要包括不考虑微裂纹之间相互作用的Taylor法,考虑裂纹之间弱相互作用的自洽法、广义自洽法、Mori-Tanaka法、微分法等,考虑裂纹之间强相互作用的统计细观力学方法。下面将采用相对较简单的Taylor法对含尺寸相同且取向均匀随机分布的微裂纹岩体进行分析,其有效弹性模量计算为 (2) 式中:E为有效弹性模量;E0为初始弹性模量;v为初始泊松比;N为单位体积内微裂纹的数量;a为激活微裂纹的平均半长度(半径)。 微裂纹半径可以通过Grady的表达式进行计算 (3) 上述有效弹性模量是统计规律下的均一化模量值,可近似把其应用到距炮孔中心距离为r的微元体所构成圆环内平均模量的变化规律。即,E(r)=f(N(r))。 根据相关研究成果[22],爆炸裂纹条数与爆炸应力波峰值成正比。即 (4) 综上可以得到爆炸应力波动态作用下的损伤因子为 (5) 爆轰气体准静态作用下损伤分布特征可参考弹性力学厚壁圆筒理论,其应力变化规律为 (6) 式中:p0j为爆轰气体准静态作用下炮孔壁压力。 假设微裂纹平均半径不变,另外动态和准静态作用的泊松比以及激活微裂纹的条数并不相同,则系数A,k也将发生变化,因此,可得到爆轰气体准静态作用下的损伤因子为 (7) 由于爆破损伤是爆炸应力波与准静态气体共同作用的结果,只不过在不同作用阶段对损伤贡献不同,实际上两者作用相互交织,相互耦合。参考潘鹏飞等的研究可得到两者共同作用下爆破损伤因子为 D(r)=1-(1-Dd(r))×(1-Dj(r)) (8) 综上,考虑爆炸应力波与准静态气体共同作用的炮孔周围损伤因子为 (9) 式中:比例系数kd,kj可通过实验或者类比法确定;不耦合装药下的炮孔壁压力峰值p0d,p0j可以参考爆炸力学中相关理论确定。 经分析爆破损伤分布特征公式发现,不耦合装药下的爆破损伤分布特征曲线变化形态基本相近,只是变化速率不同,由此造成不同的损伤范围。现特对一定的岩体参数下(静态抗压强度为50 MPa,泊松比为0.3,密度为2 600 kg/m3,纵波速度为4 000 m/s,断裂韧性为0.9 MPa·m1/2,最大体积应变率量级约为103),炮孔直径为42 mm,分别采用Φ32 mm和Φ25 mm的药卷进行爆破损伤对比分析(临界不耦合系数K0约为1.43),其分布特征曲线如图3所示。 图3 爆破损伤分布特征曲线Fig.3 Distribution characteristic curves of blasting damage 从图3可知:①不耦合装药爆破的损伤因子随距爆源距离增加呈现幂函数衰减,最终趋于0。主要由于开始阶段应力波作用较显著,对爆破损伤的贡献较大,随着应力波的衰减,准静态气体作用逐渐凸显。该理论公式充分考虑了爆炸应力波和准静态气体共同作用,可有效地表征爆破损伤分布特征,反映岩体爆破作用过程。②爆破损伤因子的衰减速率在K≥K0时呈逐渐减小的趋势,在K 援引文献[14]中的模型实验数据进行验证,其模型采用水泥砂浆试件,设计灰砂比1∶2.5,水灰比为0.4,试件密度为2 000 kg/m3,抗压强度为20 MPa,弹性波速为3 580 m/s。在单孔爆破模型实验中,装药径向不耦合系数为2.0,炮孔深度为100 mm,装药长度为30 mm,炮孔堵塞长度为50 mm,爆破损伤因子与比例距离的拟合关系如图4(实线)所示,根据文中建立的理论公式计算所得曲线如图4(虚线)所示。 图4 爆破损伤实验数据及其分布曲线Fig.4 Test data of blasting damage and its distribution curves 由图4可知:①戴俊等根据在炮孔周围介质中应力与应变随着距爆源距离的增加呈幂函数衰减规律,采用幂函数D(r)=A(r/rb)-B(A,B为反映岩石性质、装药结构、起爆条件等的系数)进行实验数据拟合,得到损伤分布为D(r)=0.625(r/rb)-1.04,且与应力、应变变化规律具有很好的一致性。②根据本文建立可以反映动态和准静态共同作用的理论公式得到D(r)=1-[1+1.300(r/rb)-1.57]-1×[1+0.048(r/rb)-2]-1,与实验数据具有很好地相关性,且可以反映爆破损伤衰减规律,同时其相关系数略高于利用幂函数拟合的相关系数,究其主要原因是爆炸应力波与准静态气体的衰减指数不同,戴俊等采用同一衰减指数进行拟合,而本文综合考虑了两者衰减规律的不同。③戴俊等认为损伤因子衰减规律与应力、应变衰减规律具有很好地一致性,从物理机制上看损伤即是岩体爆炸应力及应变作用的结果,而本文恰是从损伤细观力学有效模量入手,运用爆炸力学与弹性力学中应力衰减规律,同时考虑爆炸应力波和准静态气体共同作用下所建立的理论公式,可以初步反映岩体爆破损伤分布特征及预估损伤范围,对研究损伤特性具有重要的参考价值。 同时该分布特征曲线形式与已有的实验数据与数值计算研究成果[24-26]基本一致,可见该理论公式具有很好的适用性,不仅可以反映爆破损伤分布特征以及预估爆破损伤范围,而且可以分析爆破损伤产生的物理机制,因此具有重要的理论意义。 (1)爆炸应力波与准静态气体共同作用下的爆破损伤分布特征公式可以有效地反映爆破损伤分布规律,沟通与爆破参数的相互关系,具有很好的推广性,可方便地应用于实际工程,同时可从力学角度分析爆破损伤物理力学机制,为损伤理论研究提供参考。 (2)爆破损伤因子随着距爆源距离增加呈幂函数衰减,其衰减速率在K≥K0时呈逐渐减小的趋势,在K (3)从爆炸力学与弹性力学角度建立的损伤分布特征公式,各参数意义明确,公式形式简单,而且具有严密的力学理论基础,经过援引实验数据验证,具有较好的可行性与准确性,可以指导爆破参数优化。 (4)光面爆破或预裂爆破的装药结构应采用合适的不耦合系数,以减小爆破作用对围岩的扰动,保护岩体的完整与稳定。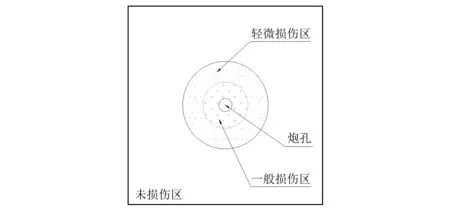
2 损伤分布特征
2.1 研究思路
2.2 理论分析





3 损伤分布特征验证与分析

4 结 论
