并联机构支链拓扑特征自动运算的算法开发

黄骏

并联机构支链拓扑特征自动运算的算法开发

黄骏

（芜湖职业技术学院机械工程学院，安徽芜湖，241006）

并联机构支链的拓扑特征能够很好地反映机构的运动维数、运动方向，但是计算过程非常复杂，学术界希望能运用计算机运算。支链信息的字符化表示方法和用于计算机判定支链间方位关系的矩阵表达式的提出是基于方位特征集的并联机构拓扑结构设计的理论和方法。依此设计的计算拓扑特征的交、并运算自动算法可实现并联机构分析的便捷化。

并联机构；交、并运算自动算法；方位特征集；支链信息。

引言

并联机构从19世纪80年代开始成为国际机构学研究的热点，与串联机构不同的是，并联机构是由两条及两条以上支链构成的闭环机构，分析过程较为复杂，人工计算的过程中不免会出现错误。随着计算机技术逐渐提高，计算机软件实现并联机构结构自动分析，可以快速、有效的得到机构所有的拓扑特征及存在性，进而根据用户需求选取合适的机构。学术界希望能够利用计算机实现拓扑结构的设计与分析的自动化，不过此项研究仍尚处于探索阶段。

Dobrjanskyj和Freudenstein教授[1]的图论理论首次将机构简图转化为机构拓扑图，实现了拓扑结构综合，也证明了通过支链实现拓扑分析的可行性。孙术华[2]根据单开链的结构组成原理，设计出了并联机构的运动输出矩阵，验证了通过计算机编程实现三平移机构自动综合的的可行性。姜珊[3]利用螺旋理论，将多维运动副转为多个单维运动副，利用VB编程软件对SolidWorks做二次开发，实现了自动分析机构自由度的功能。杨廷力教授提出的方位特征集理论[4]计算末端执行器运动自由度的数学方法简单，沈惠平教授[5]基于此理论对2~6自由度的范例并联机构进行了分析，很好的揭示了并联机构的拓扑特征（即拓扑不变量）。基于POC集理论，本文将支链信息通过数字化表达，可将其录入支链库；同时设计了交、并自动分析算法，再结合数据库中支链信息，为后面能得到所需分析并联机构的POC集等拓扑结构特征打下基础。

1. POC集理论的基本概念

并联机构的拓扑结构、方位特征集及自由度三者之间有着紧密联系，分析一个机构，必须要知道这个机构的方位特征集（POC set）[6]。POC集能够映的是运动副、支链或机构在空间上的转动维数和方向、移动维数和方向，同时在运动过程中这些维数和方向都是不会产生变化的。在方位特征集理论中，并联机构POC集的表达方式为：

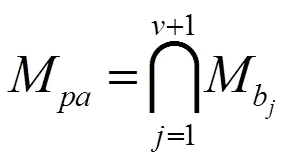
式中，Mpa为并联机构动平台上的POC集，其独立元素数不大于机构DOF；Mb为其他支链未添加时，第条单开链（SOC）支链末端构建的POC集。其中，所有支链的POC集对动平台都有同一个基点O′。

基于POC集理论，根据其机构结构性能指标来描述一个机构的性能，如公式（2）（3）可见：

POC集计算公式：

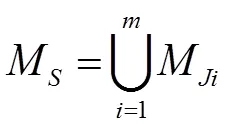
DOF计算公式：

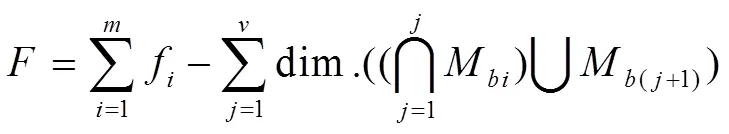
根据公式（1）（2）（3），可分析给定机构的POC集和DOF。然而，这要求学者深入学习POC集理论，方能一步步求解各个特征或参数。同时计算过程中，必须考虑每一次POC集的交、并运算，这涉及到运动副空间轴线位置关系的判定，出错概率较高。为实现拓扑结构特征的自动分析，需要设计支链上运动副轴线关系自动判定准则和拓扑特征计算过程中的交、并算法，这便能很好的解决上述问题。

2. 支链本身的信息化描述

由于并联机构是多个支链的组合，支链又可看做是多个运动副共同作用的集合，想要能实现机构的自动分析，必须将各运动副和支链的信息转化为计算机可以理解的表达，所以运动副和支链信息化描述是关键环节。

2.1 运动副的维数和方位描述

运动副主要包含以下几种：转动副（R）、移动副（P）、球副（S）和圆柱副（C）。为便于计算机理解，用下列符号反映运动副的运动方向： “”表示平行于运动副轴线方向；“#”表示垂直于运动副轴线方向的一维运动；“##”表示运动副与基点连线垂直面上的二维运动“###”表示空间三维运动。由于并联机构可以理解为是这些运动副的堆叠，所以并联机构末端执行器（看做O`点）运动的方向与运动副轴线是否共线有着必然联系，这两种位置关系下运动副的维数和方向，如表1所示。

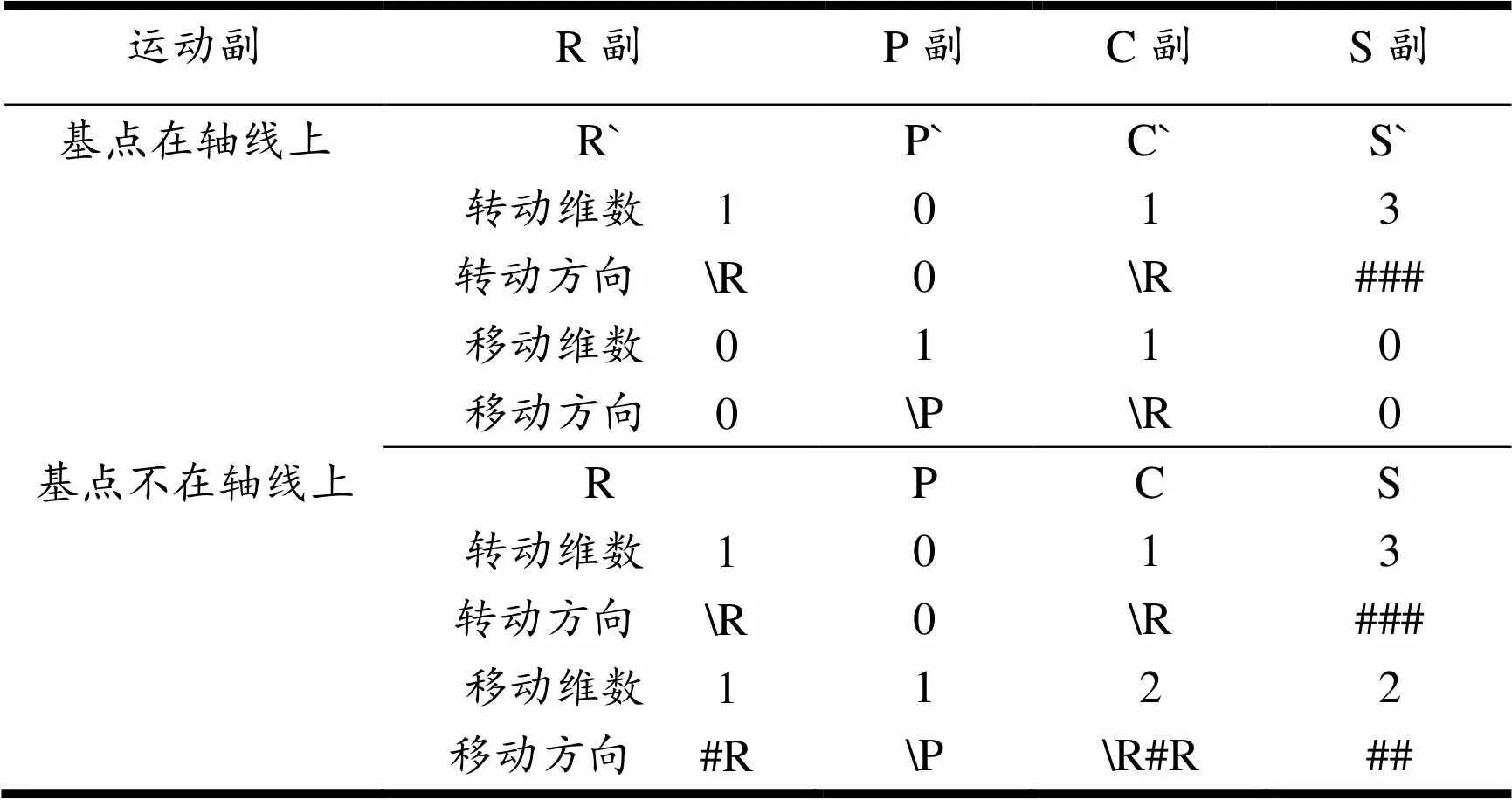
表1 运动副POC集表示方法

2.2 尺度约束的符号表示方法

运动副与运动副之间的连接关系称之为尺度约束类型，用下列符号来定义相邻运动副间的尺度约束关系： “—”表示任意连接； “|_”表示轴线垂直； “//”表示轴线平行； “/” 表示轴线共线； “*”表示轴线交于同一点； “#”表示轴线共同垂直的平面。具体表示方法如表2所示。

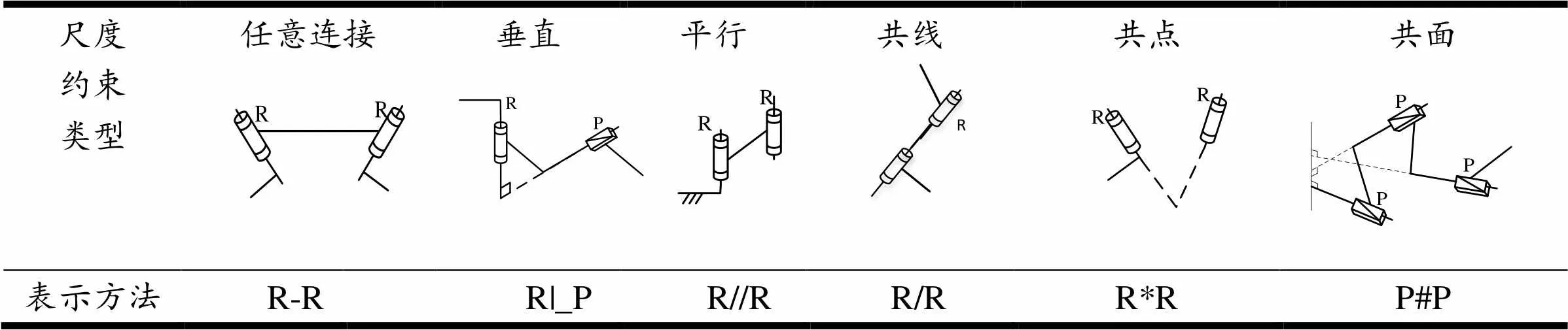
表2 相邻运动副的尺度约束类型符号表示方法

2.3 支链字符化表示

并联机构的支链是由多个运动副连接而成，支链的连接描述需要综合上述运动副和尺度约束的的表示方法，反映了从定平台开始，首个运动副至最后一个运动副的类型，以及所有运动副之间的轴线关系。

然而，表2只表示了相邻两个运动副之间的轴线位置关系，如果出现非相邻运动副尺度约束不同，就不能够准确表示出它们的方位关系。针对此种情况，表示时用“（）”表示间隔运动副之间轴线关系，这便于保证支链的唯一性和计算机录入和识别的简单性。

以图1为例，此机构是由四条相同支链组合而成，只需描述出其中一条支链与基点O`的方位关系。分析第一条支链可见，相邻运动副轴线关系为：R11与P12轴线垂直、P12与R13轴线垂直、R13与R14任意连接、R14与R15轴线共点；非相邻的运动副轴线关系为：R11和R13轴线平行；基点位于R14与R15的轴线相交处。该支链即可符号化表示为“R11(|_P12)//R13-R14`*R15`”。

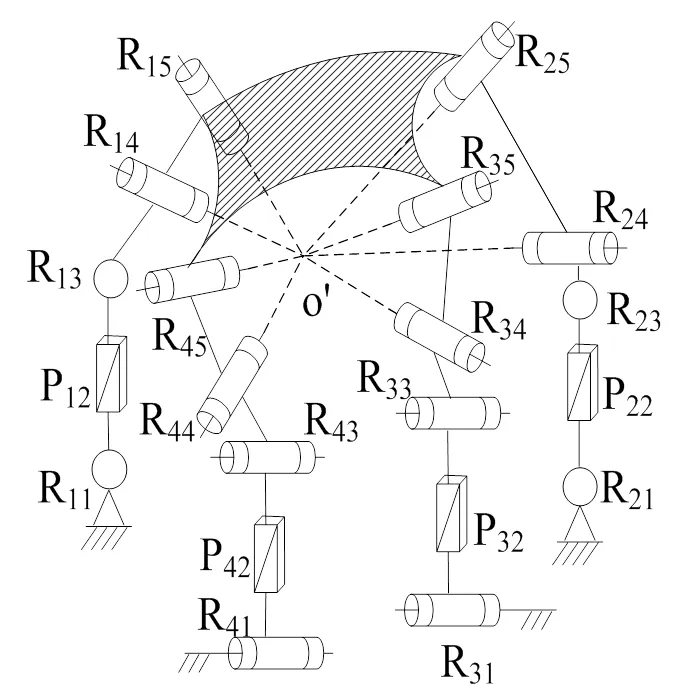
图1 间隔运动副轴线关系描述

2.4 支链间方位关系表示方法

并联机构的末端执行器运动维数和方向，可由组成机构的各支链的POC集计算得知，在做交、并运算时不可避免的要分析各支链的运动方向。人工计算可以凭借观察、经验对方向之间关系进行判断，现想实现自动分析，必须提出行之有效的自动判定方法。

在计算机程序中录入支链信息时，程序通过支链上的运动副中含有转动与移动的维数和方向进行交运算，已能得到该支链的POC集，并且支链相对基点运动的方向与支链上运动副的轴线方向有关。而计算并联机构各拓扑特征时，各支链运动方向的判定，可转化成不同支链间运动副轴线之间空间关系的判定。支链间的方位关系主要包括平行和相交，其中，相交可看做非平行，我们只需要判断支链与支链间的转动或移动方向是否平行即可。

2.4.1支链间运动方向的自动判定算法

首先，明确支链间存在的方位关系归纳为平行和非平行，即判定并联机构各支链间的转动方向和移动方向是否存在平行，须将整个过程分成转动方向判定和移动方向判定两个部分，。

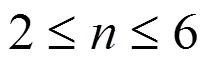
最后，依照上述支链组合，可以建立支链间转动（移动）方向平行判定表，具体如表4所示，可用R和T来代表行中的支链与列中的支链在转动和移动方向上平行关系，给矩阵R[6,6]和T[6,6]赋值，分别用0或1来表示，0代表非平行，1代表平行。这便于特征计算过程中，快速调用各支链间的方位关系。

2.4.2人工辅助判定的确定准则

支链间进行交、并运算时，最难确定方向平行关系的有以下三种：（1）不在同一条支链上的运动副轴线的平行关系；（2）不同支链运动副轴线与二维运动平面的平行关系；（3）不同支链二维运动平面之间的平行关系。

表3 支链与支链间转动（移动）方向平行判定表

方位关系判断过程中可根据这两条支链的POC集维数来确定是否需要人工辅助判定，这对接下来的程序分析至关重要。令r1、t1表示一维方向上绕运动副轴线的转动、移动，r2、t2表示二维平面转动、移动，r3、t3表示三维空间任意方向转动、转动；m、n可用于表示支链POC集维数。若一条运动支链的转动维数为1，另一条运动支链转动维数也为1，用r1/r1来表示，即可得到人工辅助判定表，如表4和表5所示。

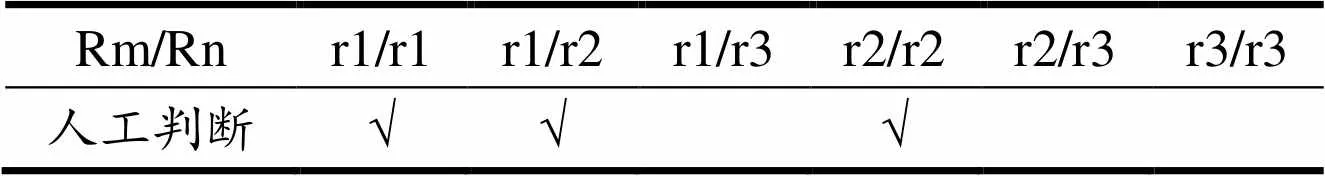
表4 支链间转动平行关系录入表

表5 支链间移动平行关系录入表

在表5和表6中，√表示需要人工判断的情况。录入表的目的是辅助完成支链间转动（移动）平行判定表。

3. 并联机构交运算和并运算的自动分析算法

数学集合论中，交集表示集合中的相同部分，并集是包含所有组合。这种数学集合的思想也同样适用于得到所有支链方位特征集的交和并运算。POC集、自由度DOF和耦合度k计算涉及到的交并运算法则分为四个部分：转动元素交运算、转动元素并运算、移动元素的交运算和移动元素的并运算，这是拓扑结构分析的基础，决定机构动平台或机构末端构件的方位信息。根据上述对运动副、支链、机构的信息化描述，可以将待分析机构中各支链的转动元素和移动元素方位信息调用出来，按下列步骤实现自动分析：

第一，设支链1为C1，是待分析机构的第a条支链；支链2为C2，是待分析机构的第b条支链。

第二，程序运行过程中，涉及到交、并运算时，直接调用支链数据库中支链1和支链2的信息，主要是维数和方向两个参数。

第三，根据支链间运动方向的自动判定算法，以及表3，得到R[a,b]和T[a,b]的值，赋值给N，可知N=0或1。

第四，若分析涉及到转动交运算，通过C1与C2的维数，结合N的数值，根据表6所示的转动交运算判定准则，可得到C1，C2这两条支链转动元素的交集，即两者相交的转动维数和转动方向，赋值给新的支链Cr，同时Cr的信息还可用于后面的交、并运算。

表6 转动交运算判定准则

第五，若分析涉及到移动交运算，通过C1与C2移动维数，结合N的数值，根据表7所示的移动交运算判定准则，可得到C1，C2这两条支链移动元素的交集，即两者相交的移动维数和移动方向，赋值给新的支链Ct，同时Ct的信息还可用于后面的交、并运算。

表7 移动交运算判定准则

第六，若分析涉及到转动并运算，通过C1与C2转动维数，结合N的数值，根据表8所示的转动并运算判定准则，可得到C1，C2这两条支链移动元素的并集，即两者相并的转动维数和转动方向，赋值给新的支链Cr，同时Cr的信息还可继续用于后面的交、并运算。

表8 转动并运算判定准则

第七，若分析涉及到移动并运算，通过C1与C2移动维数，结合N的数值，根据表7所示的移动并运算判定准则，可得到C1，C2这两条支链移动元素的并集，即两者相交的移动维数和移动方向，赋值给新的支链Ct，同时Ct的信息还可用于后面的交、并运算。

表9 移动并运算判定准则

4. 结论

为能够实现并联机构拓扑特征自动分析，将支链的方位特征和运动副轴线间的关系提供给计算机，提出了一种包含支链信息的字符化的表示方法和支链间方位关系信息化，根据机构拓扑结构分析的一般步骤，提出了用计算机实现机构结构自动分析的基本思路，针对机构POC集、自由度和耦合度等拓扑特征的自动分析，给出了具体算法。后期可根据提出的支链描述表示方法，综合了不同自由度的支链，并对其分析，建立了相对应的数据库，用于存放支链信息；为下一步分析拓扑特征时的调用提供方便，利用人机交互界面，再结合其他拓扑特征分析的算法，进而完成并联机构自动分析的软件。

[1]L. Dobrjanskyj, F. Freudenstein, Some applications of graph theory to the structural analysis of mechanisms, ASME J. Eng. Ind. 89B(1967).

[2]孙术华. 三平移并联机器人机构拓扑结构综合与位置分析[D]. 山东理工大学, 2006.

[3]姜珊. 基于编程软件的少自由度并联机构自由度计算的相关研究[D]. 燕山大学, 2013.

[4]杨廷力. 机器人机构拓扑结构学[M]. 北京: 机械工业出版社, 2004.

[5]沈惠平,尹洪波. 基于方位特征方法的范例并联机构的拓扑特征分析及其启示与应用[J]. 机械工程学报, 2015, 51(13):101-115.

[6]YANG T.L., Structural Analysis and Number Synthesis of Spatial Mechanisms[C].Proc. of the 6th World Cong. on the Theory of Machines and Mechanisms, New Delhi, 1983:280-283.

Algorithm Development of Automatic Calculation for Parallel Mechanism Featured by Branch Topology

HUANG Jun

The branch-chain topological feature of the parallel mechanism can well reflect the motion dimension and motion direction of the mechanism. But the calculation process is very complicated, and the academic circle hopes to adopt computer operations to solve this. A character representation method of chain information and the matrix expression for computer to determine the orientation relationship between branches was proposed according to the theory and method of the parallel mechanism topology design based on the Position of Characteristics (POC) sets. And the intersection and union automatic algorithms for calculating topological features are designed to facilitate parallel mechanisms analysis.

parallel mechanism;automatic algorithm for intersection and union calculation; Position of Characteristics set; branch-chain information.

TP11

A

1009-1114（2019）02-0004-06

2019-03-09

黄骏（1991—），安徽宣城人，硕士，芜湖职业技术学院助教，研究方向为并联机器人。

研究项目：芜湖职业技术学院校级项目“基于方位特征集的并联机器人结构性自动分析软件的设计研究”（项目编号：Wzyzr201916）。

文稿责编 戴晓东