圆柱体轴线直线度误差的评定及其可视化研究
2021-02-25赵新宇
赵 新 宇
(中原工学院计算机学院 河南 郑州 450007)
0 引 言
圆柱体零件是机械制造业大量使用的零件,对于高精度的圆柱孔和轴,其不仅有较高的尺寸精度要求,而且有较高的几何精度要求。圆柱体零件的轴线直线度公差是其重要的几何精度要求之一,其影响相配孔、轴的可装配性和配合性能。圆柱体轴线直线度误差的测量主要是通过沿圆柱体轴线方向测量若干圆周轮廓,并按相应的参考圆准则确定各圆周轮廓参考圆[1]的圆心坐标,将各圆周轮廓参考圆的圆心坐标逐点相连,其折线作为被测圆柱体的实际轴线,采用最小二乘法[2]或最小区域法[3-4]评定被测圆柱体的轴线直线度误差。最小区域法评定圆柱体的轴线直线度误差属于“minimax”优化问题,可用优化算法确定包容面的轴线参数。圆度、圆柱度误差的最小区域法评定以及最小外接直径、最大内切直径和最大最小直径的评定也属于“minimax”优化问题[5-9],其相关算法也可在圆柱体轴线直线度误差的最小区域法评定中应用。为了使评定结果更加直观,需要对评定结果可视化。目前,直线度误差的研究主要集中在机床导轨的空间直线度误差的测量与补偿等相关问题上,但圆柱体直线度误差的测量与评定及其可视化研究较少。本文主要以最小二乘法评定圆柱体轴线直线度误差的结果为基础,研究圆柱体轴线直线度误差评定结果的可视化,其数据处理方法同样适用于最小区域法圆柱体轴线直线度误差的评定。
1 最小二乘法圆柱体轴线直线度误差的评定模型
1.1 最小二乘圆心坐标的确定
已知第i圆周轮廓第j采样点相对径向变动量为Δij,i=1,2,…,m,j=1,2,…,n,m和n分别为圆周轮廓数和每个圆周轮廓上的采样点数。假设被测圆柱体的公称尺寸为D,则第i圆周轮廓第j采样点到虚拟回转轴线的径向尺寸可表示为:
(1)
由于圆柱体轴线直线度误差测量之前,均经过调心调平处理,将确定最小二乘参考圆圆心x和y轴坐标的非线性最小二乘问题转化为线性最小二乘问题,可得到第i圆周轮廓的最小二乘圆的圆心坐标oi(ai,yi,zi):
(2)
式中:φij为第i圆周轮廓上第j采样点与x轴的夹角,φij=(j-1)Δφ;Δφ为两相邻采样点间的夹角,Δφ=2π/n;zi为第i个最小二乘圆圆心距xOy平面的z向距离;Δz为两相邻最小二乘圆之间的z向距离。式(2)中参数含义见图1。将各最小二乘圆圆心逐点相连,即可得到被测圆柱体的实际轴线,如图2所示。

图1 第i圆周轮廓及其最小二乘圆
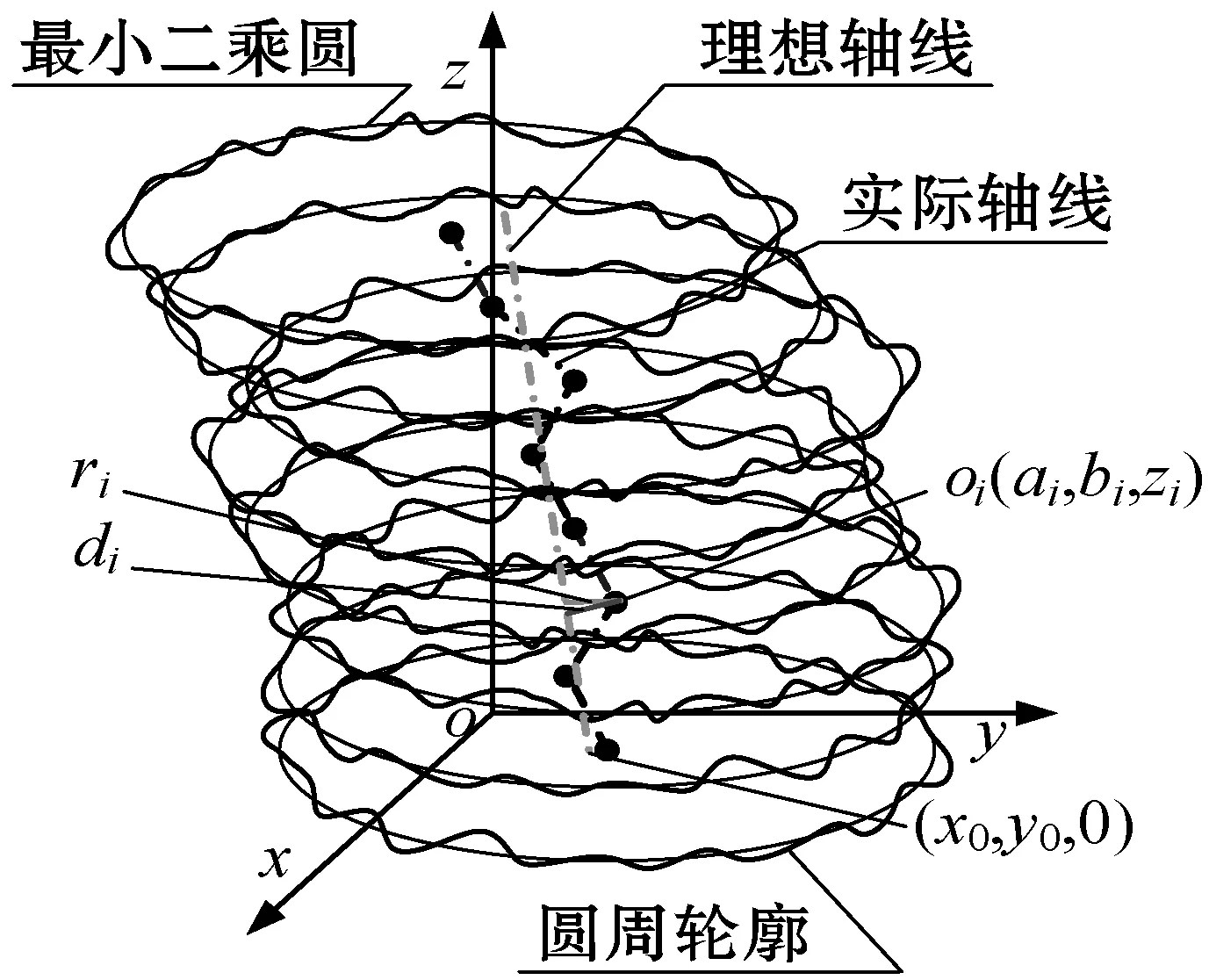
图2 被测圆柱体圆周轮廓及其轴线
1.2 最小二乘轴线参数的确定
圆周轮廓的最小二乘圆的圆心坐标oi确定后,可利用最小二乘法确定图2所示理想轴线的参数(x0,y0,p,q),其中:x0和y0分别为理想轴线一端在xOy平面上的x轴和y轴方向上的坐标;p=cosα/cosγ,q=cosβ/cosγ,α、β、γ分别为理想轴线与x轴、y轴、z轴间的夹角。依据最小二乘法的定义,理想轴线参数应满足下式:
(3)
式中:ri为第i圆周轮廓的最小二乘圆心与理想轴线之间的径向距离,可表示为:
(4)
将式(4)代入式(3),并对F分别求待定参数x0、y0、p、q的偏导,令四个偏导数分别等于零,可得到参数x0、y0、p和q的四元一次方程组,解该四元一次方程组,即可得到最小二乘理想轴线参数。
由式(5)确定第i最小二乘圆圆心到该理想轴线的垂直距离di,如图2所示。
(5)
最小二乘法评定得到的圆柱体轴线直线度误差为:
(6)
2 误差评定结果可视化
2.1 圆柱体圆周轮廓的可视化
若由式(1)计算得到的ρij将圆周轮廓显示出来,看到的将是理想圆的轮廓,圆周轮廓上的微小变动显示不出来,为此,需对微小变动进行局部放大,即:
(7)
式中:A为局部放大倍数,其大小以能在图形上清晰地显示圆周轮廓的微小变动为宜。A值过大,将使显示的圆周轮廓严重变形;A值偏小,起不到对圆周轮廓的微小变动实现局部放大的作用。圆柱体圆周轮廓图形显示如图2所示。
2.2 实际轴线的可视化
圆周轮廓局部放大后,第i圆周轮廓的最小二乘圆的圆心坐标与由式(1)确定的圆周轮廓的最小二乘圆的圆心坐标之间存在以下关系:
(8)
将由式(8)确定的最小二乘圆逐点连接起来,可近似表示为被测圆柱体的实际轴线,如图2所示。
2.3 理想轴线的可视化
将由式(8)确定的最小二乘圆圆心坐标oAi(aAi,bAi,zAi)代替式(2)确定的最小二乘圆圆心坐标oi(ai,bi,zi),按1.2节所示方法可得到圆周轮廓局部放大后的理想轴线参数(xA0,yA0,pA,qA)。用oAi(aAi,bAi,zAi)代替oi(ai,bi,zi),参数xA0、yA0、pA和qA分别代替参数x0,y0,p和q。由式(5)可得到圆周轮廓微小变动局部放大后最小二乘圆圆心到其理想轴线间的垂直距离dAi。用dAi代替式(6)中的di,即可得到圆周轮廓微小变动局部放大后圆柱体实际轴线的包容圆柱面的直径DA。理想轴线在xOyz坐标系中有三种情形,即:与z轴重合、与z轴平行、与z轴倾斜,如图3所示。
图3所示的情形是理想轴线的通常状态,理想轴线的参数为xA0、yA0、pA和qA。当理想轴线与z轴间存在倾斜时,理想轴线z之间的夹角为:
(9)
由与理想轴线与z轴间存在倾斜角γA,在包容面上作平行于xOy平面的平面,其与圆柱面轮廓的交线应是一个椭圆,椭圆轮廓的短轴长度ES等于0.5DA,长轴长度EL为:
EL=0.5DA/cosγ
(10)
椭圆轮廓的x和y坐标为:
(11)
式中:nE为椭圆轮廓上的点数;κk为椭圆轮廓上第k点与x轴间的夹角。
依据理想轴线的参数,在xOy平面将上述椭圆绕z轴逆时针旋转,旋转的角度λ为:
(12)
得到椭圆轮廓绕z轴旋转角度λ后的轮廓点的坐标为:
(13)
将上述旋转后的椭圆轮廓平移,即可得到实际轴线包容面的轮廓点的坐标为:
(14)
上述包容面的确定过程如图4所示。图4(a)所示为由式(6)确定包容面的直径DA;图4(b)所示为由式(11)确定的长半轴长EL和短半轴长ES的椭圆轮廓的x和y坐标;图4(c)所示为由式(13)获得的椭圆轮廓的x和y坐标;图4(d)为由式(14)确定的轮廓位置,得到包容面轮廓。
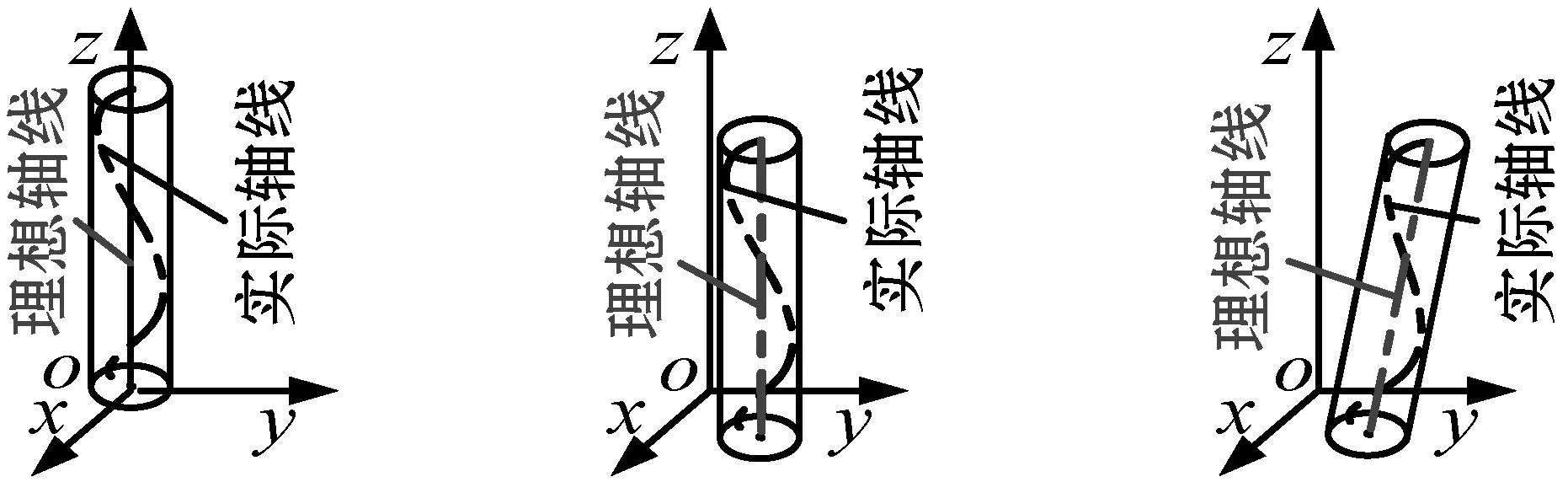
(a) 与z轴重合 (b) 与z轴平行 (c) 与z轴倾斜图3 理想轴线在xOyz坐标系中的三种情形

(a) 圆轮廓直径 (b) 椭圆轮廓坐标
2.4 程序编制
圆柱体实际轴线包容面上的每个截面的轮廓坐标确定后,可以用MATLAB中的plot3三维绘图函数与hold on语句组合使用,把m个圆周轮廓、m个椭圆轮廓、理想轴线和实际轴线呈现在一幅图上。对于圆柱体实际轴线包容面的显示,可将m个椭圆轮廓的坐标利用MATLAB中的serf或mesh函数显示。
3 实 验
使用Taylor585LT圆柱度仪对孔进行了圆周轮廓提取,并将圆周轮廓数据以“.CSV”格式导出,孔的公称尺寸D为51.5 mm,孔的测量长度Lh为100 mm,Δz等于5 mm,孔的圆周轮廓数m为21,每个圆周轮廓的采样点数n为2 000。图5-图7分别为用椭圆轮廓、surf函数、mesh函数三种可视化方法显示的孔的轴线直线度误差的评定结果以及圆周轮廓、实际轴线、理想轴线及轴线直线度误差的包容面。图中的x和y坐标并不是真实的坐标,而是微小变动局部放大后轮廓的坐标,轮廓局部放大倍数为1 000,其目的是使轮廓和轴线直线度误差的包容面更清晰,另外,没有对图中的奇异点进行处理。可以看出,三种可视化方法均能较清晰地显示被测孔的实际轴线、理想直线和包容面。但需要注意的是,轴线直线度误差较小时,图6和图7的方式将不能清晰地显示实际轴线。

图5 用椭圆轮廓显示轴线直线度误差的包容面

图6 用surf函数显示轴线直线度误差的包容面

图7 用mesh函数显示轴线直线度误差的包容面
4 结 语
本文以圆周法提取方案对圆柱体的圆周轮廓进行测量,获取圆周轮廓采样点的微小变动量,建立了基于最小二乘圆的圆心坐标的圆柱体轴线直线度误差的评定模型。由圆柱体轴线直线度误差评定模型确定理想轴线参数,建立了圆柱体实际轴线包容面轮廓坐标的生成模型,并提出了圆柱体实际轴线包容面的三种可视化方法。基于所建立的模型,编写了圆柱体最小二乘法轴线直线度误差的评定及其可视化程序,对孔的轴线直线度误差进行了评定及其结果显示。本文提出的圆柱体实际轴线包容面的可视化方法也可用于圆柱度误差评定中的图形显示。
