巧放缩，妙证明——一道数列不等式试题的证明

☉安徽省太和县第一中学 洪 振

证明数列型的不等式问题，由于其交汇性大，构造性强，思维跨度大，需要有较高的放缩技巧，因而充满思考性和挑战性，能比较全面且综合地考查学生的潜能与能力，故一直成为高考压轴题及各级各类竞赛试题命题的重要素材与考查场所.破解此类数列型的不等式问题的求解策略往往是通过多角度观察所给数列通项的结构，深入剖析其特征，抓住其式子规律进行恰当放缩，从而得以巧妙证明.

一、问题呈现

【问题】已知数列{an}的前n项和Sn满足an+1=2Sn+6，且a1=6.

（1）求数列{an}的通项公式；

本题通过数列通项an与前n项和Sn的关系式给出，可以利用变换，较快捷地确定数列{an}的通项公式.而通过数列{a}的通项公式的转化来确定数列}的特征，进n而确定前n项和Tn的关系式，转化所要证明的不等式.如何正确通过转化并利用放缩法来证明不等式＜3是本题的重点与难点，可以通过常见不等式性质加以放缩，也可以借助裂项相消法加以放缩，还可以通过数列的构造或函数的构造得到相应的不等式后再加以放缩，均能有效达到正确放缩的目的.

二、多解证明

解：（1）由已知得，当n≥2时，an+1-an=（2Sn+6）-（2Sn-1+6）=2（Sn-Sn-1）=2an，

可得an+1=3an，

又a2=2S1+6=2a1+6=18=3a1，

所以数列{an}是以a1=6为首项，公比为q=3的等比数列.

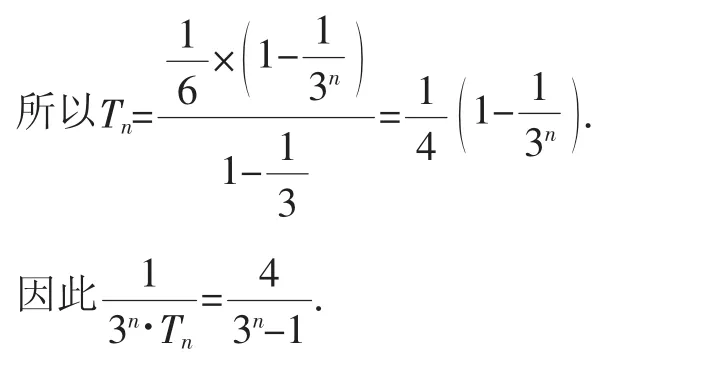
证法1：利用“Tn”的单调性放缩.

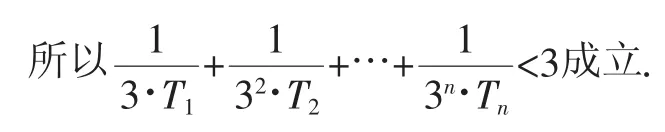
证法2：利用“糖水不等式”从第二项开始放缩.

证法3：利用“（n≥2）”从第二项开始放缩.

证法4：利用“（n≥2）”从第四项开始放缩.

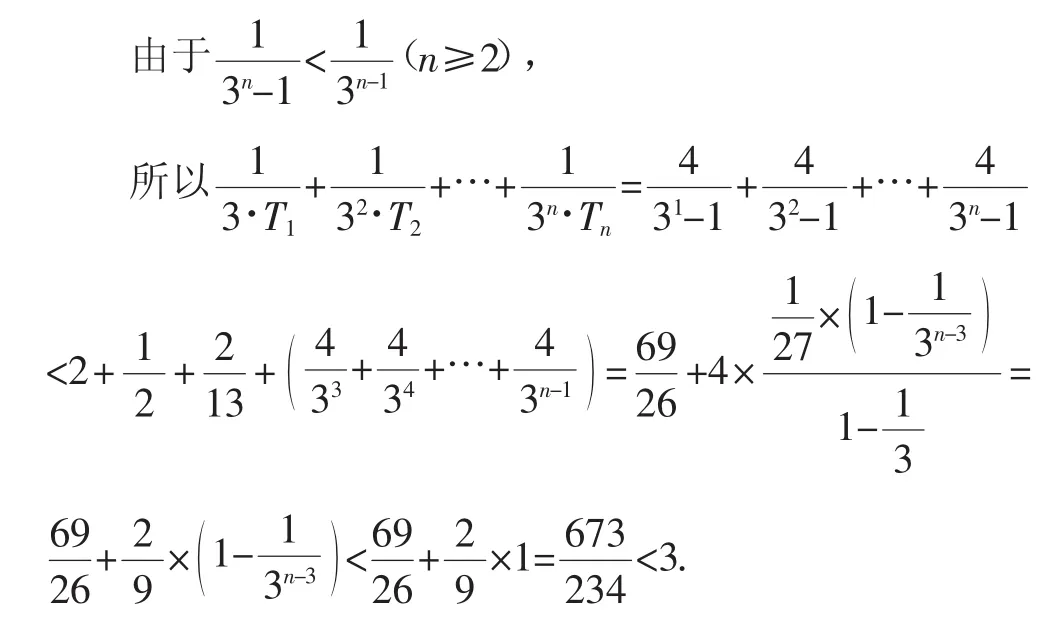
解法5：利用“（n≥2）”从第四项开始放缩

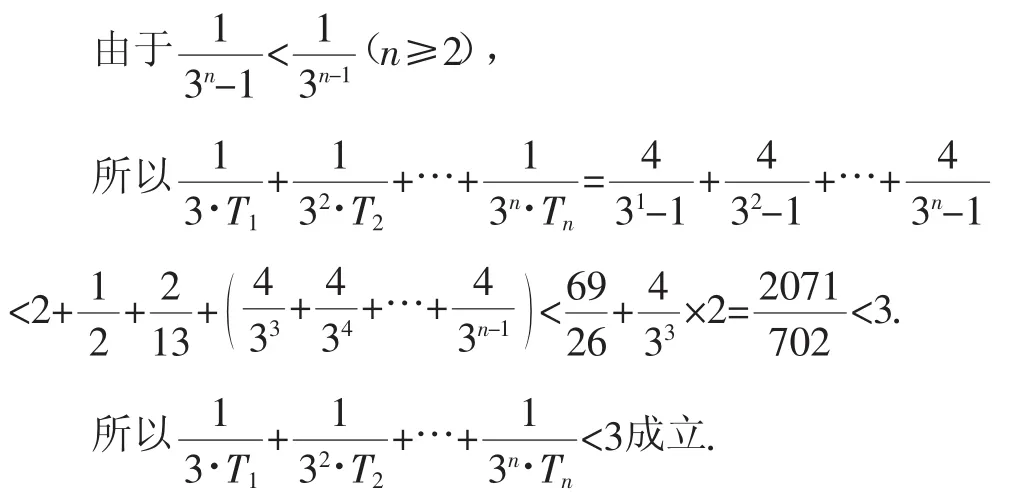
解法6：利用裂项相消法放缩

点评：借助关系式的转化与变形，结合放缩并利用裂项相消法加以转化，进而得以巧妙证明.

放缩法是证明数列型的不等式问题的一种特殊方法，利用放缩法证明数列型的不等式问题时，需要有明确的目标，才能放缩适当，其理论依据是不等式的传递性.利用放缩法处理问题时，往往是利用已知的基本不等式（如均值不等式）或某些函数、代数式的有界性、单调性等适当放缩以达到证明不等式的目的，其具体做法要依据数列型的不等式问题的结构来具体确定.W