初中数学探究性学习的课堂设计

陈秋莲

摘 要：新课程标准在强调双基学习的同时，倡导学生学习方式的转变，要让学生真正成为课堂学习的主体，要培养学生自主探究的能力和创新能力。

关键词：初中数学; 探究性学习; 课堂设计

中图分类号：G633.6            文献标识码：A      文章编号：1006-3315（2019）11-024-001

在课堂教学中教師要依据教材设计探究性问题，启发、引导学生去探究，我们的课堂设计既要考虑学生的知识结构，又要考虑教材的教学内容。在平时的教学中如何进行课堂设计培养学生的探究能力呢？我在多年的教学中做了如下的尝试。

一、一题多变，引导学生探究

在课堂教学中，根据教材内容先设计一些简单的问题激发学生思考，在此基础上将问题作一些变形，或变换问题的条件，或变换问题的形式，在变换中总结解题的方法、解题的规律，在变换中引导学生探究发现不变的共性，从而探究问题的本质。

在学习了三角形中位线定理后，我设计了如下问题

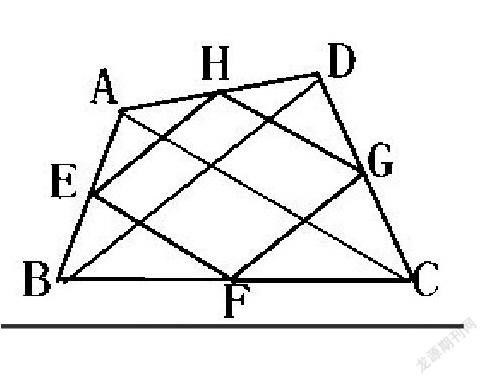
问题一：如图，四边形ABCD中，E、F、G、H分别是AB、CD、AD、BC的中点，四边形EFGH是平行四边形吗？为什么？

变式训练1.当四边形ABCD是菱形时，四边形EFGH是什么图形？

2.当四边形ABCD是矩形时，四边形EFGH是什么图形？

3.当四边形EFGH是正方形时，四边形ABCD必须满足什么条件？

分析：通过不断的变式训练引导学生探究，根据三角形中位线的性质EF=GH=1/2AC FG=HE=BD/2.EF[?]GH[?]AC EH[?]FG[?]BD，因此，中点四边形EFGH的形状和大小是由四边形ABCD的对角线AC、BD的大小、位置决定的。中点四边形EFGH的形状和大小随着AC、BD的大小、位置而变化。

二、大胆猜想，鼓励学生探究

数学教学中重视逻辑论证是完全必要的，但在实际学习过程中，许多定理（公式、法则）是靠实验、观察、操作、猜想得出结论，然后再论证，这是符合学生认识规律和心理发展特点的。学生的猜想是根据已有的知识、经验和方法，对数学问题广泛联想、积极探索的过程，大胆猜想、寻找规律是学生开展探究的前提。

在学习了全等三角形以后，我设计了如下问题：

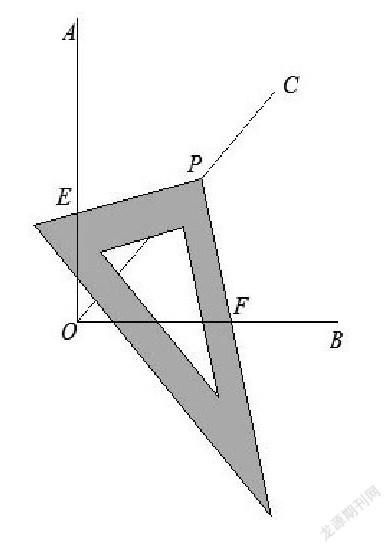
问题一：（1）画∠AOB=90°，并画∠AOB的角平分线OC。

（2）将三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边分别交于点E、F，并比较PE、PF的长度。

（3）把三角尺绕点P旋转，比较PE与PF的长度，你能得到什么结论？说说你的理由。

学生根据动手操作、观察发现：随着三角板的转动PE、PF的长度在变化，并且同时增大或减小，通过度量学生可大胆猜测PE=PF。

这样鼓励学生大胆猜测，引导学生探究怎么证明PE=PF，从而利用角平分线的性质构造全等三角形证明结论。

（4）引导学生猜想：当三角板绕着点P旋转到PE与OA垂直时，线段OE、OF与OP有什么数量关系？

（5）变式训练：当三角板绕着点P旋转到PE与OA不垂直时，猜想（4）中的结论还成立吗？请予证明。

由特殊情形变换到一般情况，引导学生猜想、探究。最后加以证明。

三、提供开放性问题，创建探究平台

每个学生都有各方面的知识潜能，但每个学生都有个性差异，根据学生的知识结构，提出一些开放性的问题提供给学生思考，不同层次的学生从不同的角度去探究，会得出不同的结论。

在复习函数时我提供了这样一个问题：

问题一：已知函数的图像经过A（1，4）和B（2，2）两点，试写出满足上述条件的不同类型的函数表达式。

分析：在初中阶段学生认识的函数有三种类型：一次函数、反比例函数、二次函数，学生可以从三种不同的角度来探究。

在学习列方程解应用题时，我提供了这样一个问题：

问题二：一辆汽车从A地驶往B地，前[13]路段为普通公路，其余路段为高速路段。已知汽车在普通公路上行驶的速度为60km/h，在高速公路上行驶的速度为100km/h，汽车A地到B地一共驶了2.2h。

请你根据以上信息，就该汽车行驶的“路程”或“时间”，提出一个用二元一次方程组解决的问题，并写出解答过程。

分析：在学习的过程中，提出问题往往比解决问题更有价值，通过审题，学生可从路程、时间不同的角度来提出问题，学生可以问：普通公路、高速公路各有多少千米？也可问：汽车在普通公路、高速公路各用了多少小时？通过探究不同层次的学生会提出不同的问题。

苏霍姆林斯基说：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望感到自己是一个发现者、研究者、探索者。”这表明：每个学生都有探究的意识和潜能。因此，在课堂教学中，我们必须通过问题的设计来引导、激发学生去探究。然而，学生的探究受到了课堂时间和空间的限制，因而，课堂设计应该紧密结合教材，贴近学生实际，应该在夯实双基的基础上，引导学生探究。