以准备性学习材料建模,理解和倍问题的数量关系
2019-04-27梁刚温彩娥
梁刚 温彩娥

摘 要:和倍问题在小学数学里一直属于奥数知识的范畴,学习简易方程后列方程解题虽然能很好地摆脱算术思维的局限性,变逆向思维为顺向思维,还有未知数参与计算等于多了已知条件等优势,但对于和倍问题部分学生依然没能顺利解决。我们通过不断尝试,打破列方程解题注重找等量关系的常规,以准备性学习材料入手,结合字母表示数的知识从旧的数学模型“已知两个数的倍数关系和其中的一个数,就能算出另一个数”迁移到新的数学模型“已知两个数的倍数关系与它们的和,就能算出这两个数”,帮助学生理解和倍问题的数量关系,收到了显著的效果。
关键词:和倍问题;建模思想;数量关系
人教版小学数学五年级上册第五单元《简易方程》里实际问题与方程的例4,是奥数知识里的和倍问题,这一类问题含有两个未知数,是学生之前从未接触过的,对于理解能力稍弱的学生来说,碰上这类题如同“老鼠拉龟”,无从下手。这类题目跟其他题目最大的不同,也是最大的难点在于,题目给出的两个数字:两个数的倍数关系与两个数的和,不能直接拿来列算式!无论用算术思路还是列方程求解,都必须明确有倍数关系的两个数里,一倍数占一份。按说五年级的学生利用中低学段学过的总数除以份数等于每份数、谁是谁的几倍等知识应该能解决这类问题的。但实际上学习列方程解决例4时,学生会设陆地面积为x,海洋面积也会用2.4x表示,可列出来的方程却是2.4x=5.1,就算旁边的同学提示,要加上陆地面积这个x才是地球的表面积,就算看着线段图来分析,他们还是一知半解。有倍数关系的两个数利用它们的和或差计算的时候,必须用上“一倍数”,但学生在“谁是谁的几倍”这句话里,往往只注意几倍数的份数,忽略了“一倍数”也占一份。
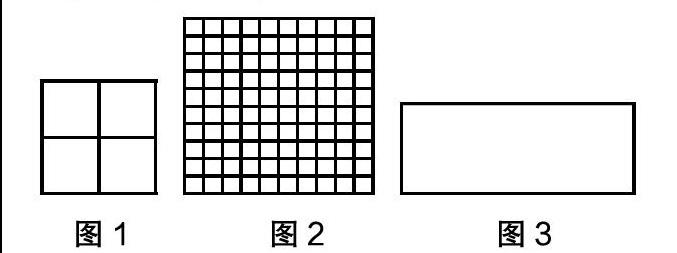
俞正强老师说:“学习困难的发生一定是有原因的。大多数学生完成小学数学学习应该不会有太大困难,如果发生了困难,一定是某个地方的准备出问题了,教师的任务就是找寻那个节点,只要节点解决了,学习也就解决了。” [1]那么和倍问题的“节点”在哪儿?应该给予学生怎样的学习准备呢?一开始我们利用三道涂色题帮助学生理解和、差、倍问题的数量关系。第1题:(图1)把其中的一份涂上颜色;空白部分的面积是阴影部分面积的( )倍。第2题:(图2)图中有100个小格,请你把其中的一部分涂上颜色,使空白部分的面积是阴影部分面积的4倍。第3题:(图3)分一分,涂一涂,使图中空白部分的面积是阴影部分面积的5倍,空白部分面积比阴影部分面积多4份。
这三道涂色题不仅帮助学生正确区分“谁是一倍数”“谁是几倍数”,也很好地强调出一倍数的地位,两者之和的总份数要加上这1份,两者相差的份数要减掉这1份,可惜对于新课和倍问题的解决帮助不大,学生不懂得把图例中的和倍关系与实际问题中的和倍关系联系起来。
我们又试着利用线段图帮助学生理解和倍问题的数量关系,发现学生计算整数倍时又对又快,换成小数倍就不行了。这反映出由整数倍过渡到小数倍,学生的观念一下子转变不过来,因为学生最早接触的份数概念、倍数概念都是整份的,把不够一份的零点几份参与计算对于学生来说有点抽象。但更深层的原因是,学生还没有真正领悟到和倍问题的解题方法,他们只是把答案套进去而已。和倍问题是在“谁是谁的几倍”的基础上进行学习的,学生对“已知两个数的倍数关系和其中一个数,就能求出另一个数”已经很熟练了,现在上升为有倍数关系的两个数都不知道,搭建一个什么桥梁才能使学生发现这两个数的和包括了一倍数和几倍数的总份数,从而利用这个数量关系来解决问题呢?
经过不懈的努力,我们终于找到了方向,把学习重点定为建立“几倍数+一倍数=和”的数学模型。要提炼模型,在“知识”与“数学问题”之间需要情境,尤其是熟悉的生活情境,更能引起学生的共鸣。于是新课引入我们创设了买水果的情境:周末老师去买两种水果,共20个,其中橘子的个数是橙子的4倍,你能猜出老师买的橘子和橙子分别是多少个吗?这道题大多数学生不能一下子找到答案,旨在建立一个初步印象:知道了两个数的和以及这两个数的倍数关系,能算出这两个数分别是多少吗?
接着开展小活动,回顾旧知“已知两个数的倍数关系和其中一个数,就能求出另一个数”。先请一个男生上台,使女生的人数是男生的3倍,要请几个女生上台?怎么列式?可以用什么方法表示这种倍量關系?让学生各抒己见,预设学生会画符号、画线段图表示人数……再请2个男生上台,女生的人数仍然是男生的3倍,要请几个女生上台?怎么列式?还能用刚才的图例表示现在的倍量关系吗?随着数量的增多,一个符号表示一个人还方便吗?此处优化方法,突出线段图的优势,可以用一段表示男生人数,仍然画三段表示女生人数。也就是说,不管男生有多少人,都是一份,叫作一倍数,同时指着3倍:只要知道两个数的倍数关系和一倍数,就能算出女生人数。女生的人数不止一倍,我们叫作几倍数。反过来,已知两个数的倍数关系和几倍数,能求出一倍数吗?总结模型:已知两个数的倍数关系和其中的一个数,就能求出另一个数。(板书省略)
接着进入重点环节,利用旧模型与字母表示数的知识,建立新模型。在刚才的活动中,女生的人数是男生的3倍,屏幕上红色箱子里乒乓球的个数也是黄色箱子的3倍。箱子里有几个乒乓球,知道吗?你有办法表示两个箱子里分别有几个乒乓球吗?(板书:x和3x,写在刚才模型的下方)反过来可以吗?用x表示几倍数的话,一倍数怎么表示?你觉得哪一种表示方法更方便?让学生加深印象:用x表示一倍数,几倍数是它的几倍就乘几更简便。此时此刻你最想知道什么?(箱子里有几个乒乓球)你能算出来吗?(不能,条件不够)那么已知两个数的倍数关系,再补充一个什么信息,就能算出两个箱子里分别有几个乒乓球?让学生开展小组活动,一起讨论交流,预设学生汇报情况有三:
(1)补充黄色箱子乒乓球的个数,能算出红色箱子乒乓球的个数。
(2)补充红色箱子乒乓球的个数,能算出黄色箱子乒乓球的个数。
(3)补充两个箱子里一共有几个乒乓球,能分别算出两个箱子里有几个乒乓球。
重点放在第(3)种情况:补充谁跟谁一共的个数,真的能算出两个箱子里分别有几个乒乓球吗?怎样列方程?谁会解这个方程?一个数算出来了,另一个数呢?
小结:原来只要知道了两个数的倍数关系,又知道这两个数的和,就能算出这两个数,总结得出新模型(图4):几倍数+一倍数=和。并追问除了上面3种方法,还有不同的方法吗?
然后巩固新模型,看线段图找信息:乙是甲的3.4倍,甲、乙一共是8.8米,让学生联系新模型,明确甲是一倍数,乙是几倍数,甲、乙分别是几知道吗?如果用x表示甲,那么乙怎么表示?看着线段图,你会列方程吗?你会解这个方程吗?甲数算出来了,乙数呢?
最后利用模型学以致用,解决实际问题:(1)地球的表面积为5.1亿平方千米,其中海洋面积约为陆地面积的2.4倍。地球上海洋面积和陆地面积分别是多少亿平方千米?(2)今年春节,年初一至年初七来六祖故里旅游的人数多达40.5万人。其中成人人数大约是儿童人数的3.5倍。你知道六祖故里旅游区这7天分别接待了多少名儿童和成人吗?
按照这个教学流程上课,学生完成这两道實际问题的准确率大大提升,可见“几倍数+一倍数=和”这个模型的建立对于学生解决和倍问题大有帮助。纵观整节课,我们利用准备性学习材料,帮助学生梳理清楚旧知识的脉络,概括总结出“已知两个数的倍数关系和其中一个数,就能求出另一个数”,在此基础上引出新问题:这两个数都未知的话,可以补充一个什么信息,就能算出这两个数?同时结合用字母表示数的知识,渗透两个未知数如何列方程解答,一步一步有梯度地层层递进,这样设计不仅突出了两个数的和,也突出了两个数都是未知数,跟例4的联系非常紧密。有了这个准备环节的铺垫,学生解决例4这种类型的题目,等量关系找得很准,列方程基本没问题。从学生的课堂回答和练习效果来看,这样设计很符合学生的认知规律,把“窍门”弄明白后,不仅和倍问题解决了,差倍问题、和差问题也能举一反三地跟着解决,对学生形成系统的数学思想很有帮助,是卓有成效的。
“知识是有类型的,每一种类型的知识, 其教学是有不同样式的。” [2]作为老师我们要努力把握好每一类知识的侧重点,通过准备性学习材料降低学习新课的坡度,帮助学生更好地理解、掌握新知识,树立学好数学的信心,感受运用数学知识解决问题的乐趣!
参考文献:
[1] 俞正强. 教学应该发生在恰当的地方——对学困生问题的20年思考与感悟[J]. 人民教育,2009(11):39-40.
[2] 俞正强. 俞正强:小学生数学课堂学习之基本样式[J]. 中国教师,2014(13):20-22.
