建立异分母分数加法法则教学设计
2019-04-27孟莹张昆
孟莹 张昆
摘 要:在实际教学中,我们很多时候只关注问题的表面现象就进行直接的教学,并没有抓住问题的本质特征,从而损伤了知识的教育(学)价值。众所周知,本质是比较单一、稳定、深刻的东西。当我们抓住一道数学题目的本质特征时,也就找到了解决这道题目的突破口,从而体悟数学之美,同时也可以引导学生不只是“知其然”,更是“知其所以然”,从而激发学生学习数学的兴趣。
关键词:现象与本质;辩证意识;异分母分数加法;计数单位
毛主席說,“我们看事情必须要看它的实质,而把它的现象只看作入门的向导,一进了门就要抓住它的实质,这才是可靠的科学分析方法”。毛主席又说,“感觉到了的东西,我们不能立刻理解它,只有理解了的东西,才能更深刻地感觉它。感觉只解决现象问题,理论才解决本质问题”。这就是说,我们解决问题、完成工作,总是要透过现象深入本质。由于数学知识的抽象化特点,这在指导学生的数学学习中显得特别重要。“现象与本质”的交换是一种辩证思维的形式,数学知识内蕴含着哲学的辩证精神,因而它是培养学生辩证意识的最为优质的课程资源。
一、“现象与本质”的辩证意识的教学价值
“现象与本质”这对哲学辩证范畴的内涵具体体现在表示事物的表里及其相互关系,是反映人们对事物认识水平和深度层次的一对哲学辩证法范畴的概念。众所周知,一般情况下,现象往往会以扭曲的方式反映本质。因此,人们刚刚接触问题信息时,这些现象中的某一个信息要素都可以作为某一条解决问题或发生认识的线索在引导着我们向某一种特定的方向前进,如此可能导致将人们引入非本质的歧途上去。于是,人们解决不了问题,或者使得人们解决问题的视野处于一种偏见的状态中。由此可知,现象总是倾向于促使人们转而依据这些现象中的另一个要素所提示的线索前进,如此反复循环,直到获得关于现象的本质的那条线索,问题才能较好地被解决。因此,现象终究是引人进入本质的入门向导,人们认识事物总是透过现象深入本质,否则我们就不能认识与理解具体的事物,不能解决问题。
由此分析发现,从现象到本质的透显过程中的详细环节的展现,在数学教学活动中有着特别重要的教育意义与教学价值,它们表现在以下两个方面:其一,从现象到本质是解决一切疑难问题的根本途径,一个问题解决不了或解决得不完善的主要原因就在于解题主体往往只是在现象上打圈子,而不能深入问题的本质,这样既耽误学习者的时间,又会消磨学习者的意志,从而损伤知识的教育(学)价值;其二,实现从现象到本质所透显的过程所依据的环节是教师启发学生发生认识、解决问题的着力点,解题主体在探究解题思路时总是绕不过去从现象抵近本质的几个关键性环节,这些关键性环节正是学习者需要萌发创新的数学观念,生成解决问题的具体方法,从而形成解决问题的深度经验的关节点。
当学生在教师的启发下进行学习活动时,通过对某个问题的正确认识,学习主体就能亲身经历与体验从“现象”深入“本质”的过程。通过这一过程,一方面会将这种认识过程的经验运用于出现在他面前新的现象性问题中去,这是解决问题的心理迁移的一部分,由此可以导致其他同类现象性的问题迎刃而解;另一方面,形成了经验,从而借助从“现象”透显“本质”的经验,在生成下一次探究问题的思路时就能够更容易地产生从“现象”过渡到“本质”的心理活动,减少探究活动的心理环节,缩短探究活动的时间,从而节省解题思维活动展开的心智资源,如此,最大限度地提高学习效率。
二、从“现象”透显“本质”形成辩证意识的教学设计示例
陆游诗云:“纸上得来终觉浅,绝知此事要躬行。”俗云:“理在用中方之妙”,在数学课堂教学活动中,向学生完整地展示由现象探讨其产生外显“现象”的内隐,“本质”就尤为重要了。在课堂教学中的实现这样的目标不是一件容易的事情,它需要教师帮助学生剔除那些由现象将学生引入歧途的信息(特别注意,教师不应该将自己通过思考获得的精准过程直接交给学生),最终达到鼓励学生从“现象”(经由学生自己的抽象与概括)抵达“本质”的目的。我们看一个课堂教学中的例子:下面是两位教师借助+的计算,建立异分母分数加法法则的教学活动过程,前一位教师记为教师甲,后一位教师记作教师乙。
我们首先来看一下教师甲的关于异分母分数加法的新授课(笔者将教学过程整理抄录如下)。
在上课之前,该教师带领学生回顾了一个关于同分母分数加法的问题:将一个西瓜平均分成8份,哥哥吃了其中的2份,也就是,弟弟吃了其中的1份,也就是,进而提问,哥哥和弟弟一共吃了这个西瓜的几分之几?学生通过先前的学习经验可以得出,和的分数单位都是,这个问题就可以转化为2个加1个等于3个,也就是,所以+=。
对于该教师在上课之前抛出这个问题作为铺垫,笔者认为:根据维果斯基“最近发展区”的理论,在学生的后续学习中,这些知识就会成为已经形成的心理机能的发展水平,为学习异分母分数加法的相关知识打下基础。紧接着,该教师向学生讲授了异分母分数+的计算方法(说明:文中省略号代表学生在进行思考)。
师:同学们,我们来看一下+这道题目该如何进行计算呢?
生:……
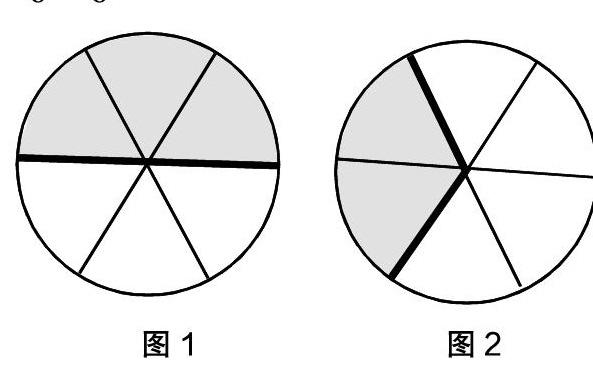
生1:我们可以通过画图的方法来解决这个问题。首先,我们拿出两张同样大小的圆形纸片,将其中的一张圆形纸片对折,也就是将这个圆形纸片平均分成2份,把其中的一份涂上颜色,用来表示;紧接着,将另一张圆形纸片平均分成三份,把其中的一份涂上颜色,用来表示。通过观察可以发现,把第一张圆形纸片平均分成6份,阴影部分占其中的三份,可以用来表示;同样的,也可以延长第二个圆形纸片的三条平分线段,把这个圆形纸片平均分成6份,阴影部分占其中的2份,可以用来表示。通过先前的知识学习,可以得知=,=,所以+=+=。(图1、图2)
师:这位同学采取了数形结合的思想方法,把符号语言转化为图形语言来解决这个问题,那么我们还有其他的方法可以解决这个问题吗?
生:……
师:同学们如果没有什么想法的话,我们一起来看一下老师解决这个题目的思路:老师有12个苹果,把它们平均分成两组,每组各有6个苹果,老师拿出第一组的3个苹果给了李红同学,拿出第二组的2个苹果给了王明同学,李红同学和王明同学所得苹果分别占他们各自组的和,我们知道=,=,要想求这两位同学所得苹果的总数占全部苹果数的多少,可以进行如下计算:+=+=。
(随后,该教师对于异分母分数加法的算理进行了讲解。)
师:对于异分母分数的加法来说,我们可以先把这两个分数进行通分,然后按照同分母分数的加法法则进行计算。
从教师甲的教学方法不难看出,他只看到了这个问题的表面现象。教师甲先将这两个分数进行了通分,再按照同分母分数的加法法则进行计算,他没有看到异分母分数加法的本质:要找到这两个分数共同的分数单位后再进行计算。而且,以上两种计算方法都是存在弊端的:第一种是把符号语言转化成了图形语言,但是学习程度较好的学生可能会提出一些疑问,比如“为什么我们就能保证这两张圆形纸片是绝对相同的呢?”“在保证这两张圆形纸片绝对相同的前提下,我们就真的能保证把这两张圆形纸片平均分成了六份吗?”等诸如此类的问题。对于第二种教学方法,教师甲只是符合了教学“情境”的要求,学生也能听得懂,但是这种教学就像是强加给学生一些定义或者方法,只是让学生看到了问题的表面,并没有深层次地探究问题的本质是什么,学生无法探究到问题的本质,就可能会出现只知其然而不知其所以然,只会这一道题目而不是会这一类题目的情况。所以,教师甲的教并不是为了学生的学,这种教学方法并没有体现学生在学习过程中的主体地位。
在分析完教师甲的教学过程后,我们再来分析一下教师乙的教学过程。
以下是教师乙的课堂教学实录(实录中的省略号代表学生在思考)。
师:如何解决+这个问题?
生:……
师:大家看,①2支铅笔+3支铅笔=?②2支铅笔+3支钢笔=?
生1:2支铅笔+3支铅笔=5支铅笔;问题②不能进行加法运算。
师:为什么问题②不能进行加法运算呢?
生2:因为这两个物品的性质不同,所以不能合并。
师:那么,要实现两个数的加法运算,需要怎样的前提条件?
生:这两个数必须具有统一的单位。
师:这种发现对于讨论+的计算方法是否有帮助呢?我们具体来看下这一类问题。我们知道,在整数加法中有2+3=5,为什么这个式子可以进行计算,是因为它们的计数单位都是1;在小数加法中0.2+0.3=0.5能够进行计算,是因为它们的计数单位都是0.1。那么据此类比,同学们对于解决这类问题有什么想法呢?
生3:我们得想办法找到与的一个统一的单位,并且使与在这个统一的单位下都变成整数,从而变不同的单位为相同的单位,变分数为整数。
师:生3同学的这种设想可以办到吗?
生4:办得到。我们可以把看作由以下数据组合而成:2个,3个,4个,5个,6个,……同样的,可以把看作由以下数据组合而成:2个,3个,4个,5个,6个,……
师:生4同学通过拆分得到的结果对于讨论+的计算方法有帮助吗?
生5:通过观察比较,我们可以看出,和有共同的分数单位或……因为=3个,=2个,因此,求+的和就可以看作是求3个与2个的和,所以这个问题就从求两个异分母分数的和转化成了求两个计数单位相同的正整数的和。同理,因为=6个,=4个,因此,+也可以看成是求6个与4个的和。
师:也就是说,+=3个+2个=5个=,或者+=6个+4个=10个==。
接着,基于所得到的结论,教师乙鼓励学生得出异分母分数加法的“通分”法则的学习过程等。(具体活动过程略)
我们可以看出,教师乙的教学抓住了这个问题的根本性质,也就是找出了两个异分母分数之间共同的计数单位。它是由产生加法的先决条件所决定的,所谓加法的先决条件,就是指“具有相同单位的多项数据可以简要地合并成一项”,这就是异分母分数加法法则产生的内在本质。教师乙通过创设问题情境,诱导学生认识到可以实现加法法则的本质,进而启发学生找到具体的途径,将异分母分数加法中的每一个加数都转化成了在某个计数单位下的正整数,这样就可以进行相应的合并了。剩下的问题(包括“异分母分数加法法则的建立”)都是技术性的问题,而不是概念性的问题了。同时,学生经由教师乙的教学活动方式所得到的知识与经验可以顺利地迁移到新的数学运算中去(如合并同类项、合并同类根式等)。由此可见,教师乙的教学活动方式是优于教师甲的。
因此,通过教师甲与教师乙建立异分母分数加法法则的现实教学活动过程,我们发现:在教学准备工作中,教师一定要仔细分析数学知识,从中找出知识具体的特点;接着根据这个特点,深入知识的本质;然后根据问题的本质,分析学生对这个知识点的认识的心理活动过程,并选择相应的教学情境,设计教学活动,力图引导学生从数学化问题的现象性信息的心理过渡到问题的本质,从而增加教学的有效性,发挥知识的教学价值,实现数学教学目标。
三、简要结语
数学教学所要传授的数学知识相对固定(其最低限度已经写入数学课程标准),但是,选择怎样的传授途径来进行课堂教学活动,却非固定不变。它随着教师所吸收的教学理念的不同、持有的教学观念不同、预设的教学目标不同、获得的教学经验不同、支持教学活动的媒体不同、对数学知识性质的理解不同、对学生认知活動途径的把握不同等,存在着多种选择。不同的教学设计对促成学生发展的结果大相径庭,更让数学教学目标的实现迥然有别。数学教师要完善自己的教学行为,获得良好的教学效果,就不应该拘泥于教科书的安排,而是要依据知识的具体特点,让学生发生具有具体特点的知识认识时的具体心理特点,用教材教而不是教教材。如此,才能发挥数学知识的教学价值,实现教学目标。我们所举的例子很好地说明了这种教学观念。
