基于核心素养培育的小学数学教学案例

杜成秀 梁玲玲

摘  要：以“三角形的三边关系”为例，以教学片段的形式，对六个核心素养中的数学抽象、直观想象、数学分析、逻辑推理的培育和落实给出具体的实践和初步的思考。

关键词：三边关系;数学抽象;直观想象;数学分析;逻辑推理

《普通高中数学课程标准（2017年版）》指出了六个数学核心素养，分别是数学抽象、直观想象、逻辑推理、数学运算、数学建模、数据分析。一线教师在教学中对学生进行核心素养的培育是一个长期的过程，我们不可能通过一节课实现很高的要求，最起码应该有这样的意识。那么，如何在日常教学中对小学生进行核心素养的培育呢？本文以“三角形的三边关系”一课为载体，通过观察、操作、比较、归纳、推理等方式初步尝试进行小学数学核心素养的培育。下面进行简单介绍，不当之处，敬请指正。

一、教学片段1：数学抽象

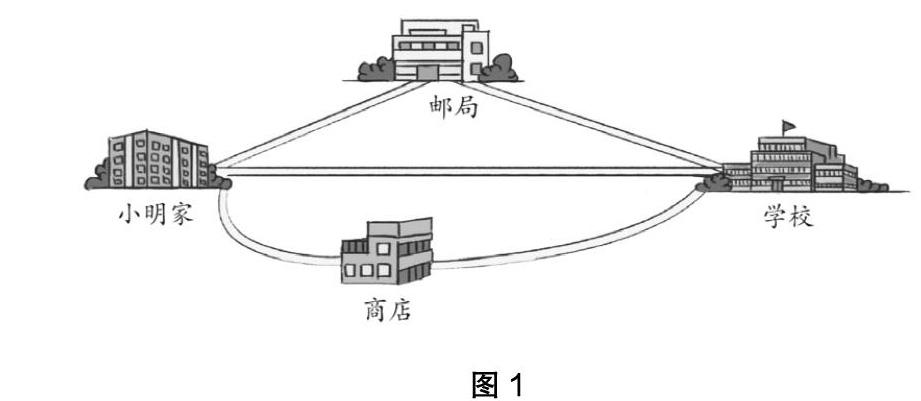
师：同学们，这是小明家到学校的路线图（见图1），他可以怎样走？如果是你，你会走哪一条？为什么？

学生根据情况回答。

师：在数学上，我们可以将小明家和学校看成两个点，在这两点之间的所有连线中，线段最短。这条线段的长度叫作两点间的距离。把邮局也看成一个点，这3个点连在一起就形成了我们学过的三角形。

分析：史宁中教授说：“用数学的眼光观察现实世界。”在课前引领学生将现实生活中的房屋（学校、家、邮局），看成数学上的一个点来进行研究。这一过程既是教学的需要，也是培养学生用数学眼光观察现实世界的素材 [1]，所以，通过这一过程帮助学生体会抽象思想的运用。

二、教学片段2：直观想象

师：同学们，老师给大家准备了两条线段，你能围成一个三角形吗？

生：将其中一条剪开，这样就变成3条线段了。

师：请将其中的一条沿刻度线剪开，就可以去围三角形。那其中一条线段便是三角形两条边的和。下面请2人一组记录下各线段的长度和围的结果。

学生分组操作，记录结果，如下表（见表1）。

师：好，老师看大家操作基本完成了，都围成三角形了吗？

生1：我的围成了。

生2：我的没有围成。

师：通过操作，我们发现可以将得到的3条线段，分成能围成三角形和不能围成三角形两种情况。（板书：能，不能）

分析：直观想象在数学教学中是比较常见的，在直观想象的基础上，结合实际操作可以更加明确研究目标和方向 [2]。本节课中，学生在动手操作的基础上发现：3条线段，有的能围成三角形，有的不能围成三角形。这样，便建立了唯一的分类标准：能围成的、不能围成的，为下一步研究指明了方向。

三、教学片段3：数据分析和逻辑推理

1. 不能围成的情况

师：我们先请不能围成的小组给大家汇报他们围的过程及结果。请一位同学在投影下展示，一位同学将结果记录在黑板上。

小组展示，并获取数据。

师：不围成的，还有其他情况吗？我们观察这些不能围成的数据，你有什么发现吗？

生1：（手指着数据）这两个数加起来比这个数小。

生2：（手指着数据）这两个数加起来和这个数一样大。

师：看来，当这两条边的长度加起来不如另一条边长;或者，这两条边的长度加起来和第三条边一样长的时候不能围成三角形。也就是，当两条边的和小于或等于第三边时，不能围成三角形。

师：好，请没围成的同学再验证一下你们刚才记录的数据，是不是也有两边的和小于或等于第三边。有不符合的吗？

2. 能围成的情况

（1）初步分析

师：下面有请围成的同学，给大家展示围的过程和结果。同样，一位同学在投影下展示，一位同学将结果记录在黑板上。

小组展示，并获取数据。

师：观察能围城的这3组数据，你有什么发现？先自己想一想，然后和你的同桌互相说一说。

生：（手指着数据）这两个数加起来比这个数要大。（根据具体情况板书一个不等式）

师：也就是说，这时候两边的和要大于第三边。谢谢这位同学，他发现只要两边之和大于第三边就可以围成三角形。

（2）质疑补充

师：真的是这样吗？两边之和大于第三边，一定能围成三角形吗？借助黑板上的5组数据，同桌两人交流一下。

生：我发现，不能围成的这些数据中有的两边加起来也比第三条边大。

师：太棒了！掌声感谢他！那看来，只判断一组还不够，得判断3组。（以刚才围成的为例，补充另外两个不等式）

师：从刚才的分析我们发现，每两条边的和都要大于第三边，才能围成一个三角形。在数学上，我们说任意两边的和大于第三边（板书：任意）。用这一个词就概括了3种情况。

师：我们来一起验证一下黑板上另外2组数据。

师：现在，请围成的同学再验证一下你们刚才记录的数据，是不是也符合任意两边的和大于第三边。

（3）进一步验证

师：刚才，我们一起验证的都是一些整厘米的数据，发现任意两边的和都大于第三边。那是不是所有的三角形，边长不是整厘米的那些也满足呢？我们借助几何画板来看一下（见图2）。

师：你有什么感受吗？

生：很多三角形都满足任意两边的和大于第三边。

师：嗯，正如你说的，验证了这么多三角形，我们可以说所有的三角形都满足任意两边之和大于第三边。

分析：华罗庚说：“数缺形时少直观，形缺数时难入微。”本节课便是“借数入微”“以数解形”的具体实例，通过一系列的数据分析，成功将三角形的三条边的关系转化为寻找边的长度的关系。这也是学生由三边围成三角形的概念认识三角形，到更深入了解三角形特性的过程。在学习过程中，可以帮助学生体会数学知识的学习是不断细致、不断深入的过程。

在本部分学习时，还运用了逻辑推理。由于小学阶段的几何学习多以实验几何为主，所以逻辑推理是小学数学中容易忽视的一种方法 [3]。在三角形三边关系的教学中教师是比较少运用的，但笔者认为，应把握好每一次培育学生严密思维的机会。本节课在能围成和不能围成的教学即将结束时，借助2个追问：验证以下黑板上另外2组数据是否满足？请不能围成（或围成）的同学再验证一下你们刚才记录的数据，是不是也符合？以及几何画板这一信息技术，对逻辑推理这一核心素养的培育进行了有益的尝试。

综上，本节课在教学中尝试对学生进行数学抽象、直观想象、数据分析和逻辑推理等核心素养的培育，上述做法未必准确，更不一定正确，欢迎更多的一线教师积极参与进来，开发出更多优秀的案例，为小学数学核心素养的实践研究做出一定的贡献。

参考文献：

[1]  管小冬. 注重经历过程 发展问题意识——“三角形三边的关系”教学片段与思考[J]. 小学数学教育，2018（12）：47-49.

[2]  宋煜阳. 关于“三角形的认识”的认识 （上）[J]. 小学数学教师，2018（5）：52-55.

[3]  姚麗华. 基于平板技术辅助的课堂教学探索——“三角形的内角和”教学实录与思考[J]. 教学月刊小学版（数学），2018（z2）：13-16.